Regresja logistyczna jest nadzorowany algorytm uczenia maszynowego używany do zadania klasyfikacyjne gdzie celem jest przewidzenie prawdopodobieństwa, że ​​instancja należy do danej klasy, czy nie. Regresja logistyczna to algorytm statystyczny analizujący związek między dwoma czynnikami danych. W artykule omówiono podstawy regresji logistycznej, jej rodzaje i zastosowania.

Spis treści

• Co to jest regresja logistyczna?
• Funkcja logistyczna – funkcja sigmoidalna
• Rodzaje regresji logistycznej
• Założenia regresji logistycznej
• Jak działa regresja logistyczna?
• Implementacja kodu dla regresji logistycznej
• Kompromis w zakresie precyzji przywołania w przypadku ustawienia progu regresji logistycznej
• Jak ocenić model regresji logistycznej?
• Różnice między regresją liniową i logistyczną

Co to jest regresja logistyczna?

W przypadku danych binarnych stosuje się regresję logistyczną Klasyfikacja gdzie używamy funkcja sigmoidalna , który przyjmuje dane wejściowe jako zmienne niezależne i generuje wartość prawdopodobieństwa od 0 do 1.

Na przykład mamy dwie klasy Class 0 i Class 1, jeśli wartość funkcji logistycznej dla wejścia jest większa niż 0,5 (wartość progowa), to należy ona do klasy 1, w przeciwnym razie należy do klasy 0. Nazywa się to regresją, ponieważ jest przedłużeniem regresja liniowa ale jest używany głównie do problemów klasyfikacyjnych.

Kluczowe punkty:

• Regresja logistyczna przewiduje wynik kategorycznej zmiennej zależnej. Dlatego wynik musi być wartością kategoryczną lub dyskretną.
• Może to być Tak lub Nie, 0 lub 1, prawda lub fałsz itp., ale zamiast podawać dokładną wartość jako 0 i 1, podaje wartości probabilistyczne mieszczące się w przedziale od 0 do 1.
• W regresji logistycznej zamiast dopasowywać linię regresji, dopasowujemy funkcję logistyczną w kształcie litery S, która przewiduje dwie wartości maksymalne (0 lub 1).

Funkcja logistyczna – funkcja sigmoidalna

• Funkcja sigmoidalna to funkcja matematyczna używana do mapowania przewidywanych wartości na prawdopodobieństwa.
• Odwzorowuje dowolną wartość rzeczywistą na inną wartość z zakresu od 0 do 1. Wartość regresji logistycznej musi mieścić się w przedziale od 0 do 1, która nie może przekroczyć tej granicy, więc tworzy krzywą przypominającą formę S.
• Krzywa w kształcie litery S nazywana jest funkcją sigmoidalną lub funkcją logistyczną.
• W regresji logistycznej używamy koncepcji wartości progowej, która określa prawdopodobieństwo wartości 0 lub 1. Przykładowo wartości powyżej wartości progowej dążą do 1, a wartość poniżej wartości progowych dąży do 0.

Rodzaje regresji logistycznej

Na podstawie kategorii regresję logistyczną można podzielić na trzy typy:

1. Dwumianowy: W dwumianowej regresji logistycznej mogą istnieć tylko dwa możliwe typy zmiennych zależnych, takie jak 0 lub 1, wynik pozytywny lub negatywny itp.
2. Wielomian: W wielomianowej regresji logistycznej mogą istnieć 3 lub więcej możliwych nieuporządkowanych typów zmiennej zależnej, takich jak kot, pies lub owca
3. Porządkowy: W porządkowej regresji logistycznej mogą istnieć 3 lub więcej możliwych uporządkowanych typów zmiennych zależnych, takich jak niski, średni lub wysoki.

Założenia regresji logistycznej

Zbadamy założenia regresji logistycznej, ponieważ zrozumienie tych założeń jest ważne, aby mieć pewność, że stosujemy odpowiednie zastosowanie modelu. Założenia obejmują:

1. Niezależne obserwacje: Każda obserwacja jest niezależna od drugiej. co oznacza, że ​​nie ma korelacji pomiędzy żadnymi zmiennymi wejściowymi.
2. Binarne zmienne zależne: przyjmuje się założenie, że zmienna zależna musi być binarna lub dychotomiczna, co oznacza, że ​​może przyjmować tylko dwie wartości. W przypadku więcej niż dwóch kategorii używane są funkcje SoftMax.
3. Zależność liniowa między zmiennymi niezależnymi a logarytmem szans: Zależność między zmiennymi niezależnymi a logarytmem szansy zmiennej zależnej powinna być liniowa.
4. Brak wartości odstających: w zbiorze danych nie powinny znajdować się wartości odstające.
5. Duży rozmiar próbki: Rozmiar próbki jest wystarczająco duży

Terminologie związane z regresją logistyczną

Oto kilka typowych terminów związanych z regresją logistyczną:

• Niezależne zmienne: Charakterystyka wejściowa lub czynniki predykcyjne stosowane do przewidywań zmiennej zależnej.
• Zmienna zależna: Zmienna docelowa w modelu regresji logistycznej, którą staramy się przewidzieć.
• Funkcja logistyczna: Wzór używany do przedstawienia wzajemnego powiązania zmiennych niezależnych i zależnych. Funkcja logistyczna przekształca zmienne wejściowe w wartość prawdopodobieństwa z zakresu od 0 do 1, która reprezentuje prawdopodobieństwo, że zmienna zależna będzie wynosić 1 lub 0.
• Szanse: Jest to stosunek czegoś, co się zdarza, do czegoś, co nie zachodzi. różni się od prawdopodobieństwa, ponieważ prawdopodobieństwo to stosunek czegoś, co się wydarzy, do wszystkiego, co może się wydarzyć.
• Log-szanse: Logarytm szans, znany również jako funkcja logitowa, to logarytm naturalny szans. W regresji logistycznej logarytm szans zmiennej zależnej modeluje się jako liniową kombinację zmiennych niezależnych i wyrazu wolnego.
• Współczynnik: Oszacowane parametry modelu regresji logistycznej pokazują, jak zmienne niezależne i zależne są ze sobą powiązane.
• Przechwycić: Stały składnik modelu regresji logistycznej, który reprezentuje logarytm szansy, gdy wszystkie zmienne niezależne są równe zero.
• Oszacowanie maksymalnego prawdopodobieństwa : Metoda zastosowana do estymacji współczynników modelu regresji logistycznej, maksymalizująca prawdopodobieństwo obserwacji danych danego modelu.

Jak działa regresja logistyczna?

Model regresji logistycznej przekształca regresja liniowa funkcja ciągłego wyprowadzania wartości na wartości kategoryczne za pomocą funkcji sigmoidalnej, która odwzorowuje dowolny zbiór niezależnych zmiennych o wartościach rzeczywistych na wartość z zakresu od 0 do 1. Funkcja ta jest znana jako funkcja logistyczna.

Niech niezależnymi cechami wejściowymi będą:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

a zmienną zależną jest Y mający tylko wartość binarną, tj. 0 lub 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

znowu skorupa Bourne’a

następnie zastosuj funkcję wieloliniową do zmiennych wejściowych X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

Tutajx_i jest i obserwacją X,w_i = [w_1, w_2, w_3, cdots,w_m] jest wagą lub współczynnikiem, a b jest terminem odchylenia, znanym również jako wyraz wolny. po prostu można to przedstawić jako iloczyn skalarny wagi i odchylenia.

z = wcdot X +b

cokolwiek omówiliśmy powyżej, jest regresja liniowa .

Funkcja sigmoidalna

Teraz używamy funkcja sigmoidalna gdzie danymi wejściowymi będzie z i znajdziemy prawdopodobieństwo między 0 a 1, tj. przewidywane y.

sigma(z) = frac{1}{1-e^{-z}}

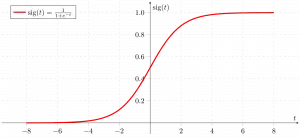
Funkcja sigmoidalna

Jak pokazano powyżej, funkcja sigmoidalna figury konwertuje dane zmiennych ciągłych na prawdopodobieństwo tj. pomiędzy 0 a 1.

• sigma(z) zmierza w kierunku 1 jakoz ightarrowinfty
• sigma(z) zmierza w kierunku 0 jakoz ightarrow-infty
• sigma(z) jest zawsze ograniczona od 0 do 1

gdzie prawdopodobieństwo bycia klasą można zmierzyć jako:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Równanie regresji logistycznej

Nieparzystość to stosunek czegoś, co się zdarza, do czegoś, co nie zachodzi. różni się od prawdopodobieństwa, ponieważ prawdopodobieństwo to stosunek czegoś, co się wydarzy, do wszystkiego, co może się wydarzyć. więc dziwne będzie:

frac{p(x)}{1-p(x)} = e^z

Stosowanie logu naturalnego na nieparzystym. wtedy log nieparzysty będzie:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

wówczas ostateczne równanie regresji logistycznej będzie wyglądało następująco:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Funkcja wiarygodności dla regresji logistycznej

Przewidywane prawdopodobieństwa będą wynosić:

• dla y=1 Przewidywane prawdopodobieństwa będą wynosić: p(X;b,w) = p(x)
• dla y = 0 Przewidywane prawdopodobieństwa będą wynosić: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Biorąc naturalne kłody po obu stronach

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Gradient funkcji logarytmicznej wiarygodności

Aby znaleźć szacunki największej wiarygodności, różniczkujemy w.r.t w,

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Implementacja kodu dla regresji logistycznej

Dwumianowa regresja logistyczna:

Zmienna docelowa może mieć tylko 2 możliwe typy: 0 lub 1, które mogą reprezentować wygraną vs przegraną, pass vs fiasko, martwy vs żywy itp. W tym przypadku używane są funkcje sigmoidalne, co zostało już omówione powyżej.

Importowanie niezbędnych bibliotek w oparciu o wymagania modelu. Ten kod w języku Python pokazuje, jak używać zbioru danych dotyczących raka piersi do implementacji modelu regresji logistycznej na potrzeby klasyfikacji.

Wyjście :

Dokładność modelu regresji logistycznej (w %): 95,6140350877193

Wielomianowa regresja logistyczna:

Zmienna docelowa może mieć 3 lub więcej możliwych typów, które nie są uporządkowane (tj. typy nie mają znaczenia ilościowego), np. choroba A vs choroba B vs choroba C.

W tym przypadku zamiast funkcji sigmoidalnej używana jest funkcja softmax. Funkcja Softmax dla klas K będzie:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Tutaj, K reprezentuje liczbę elementów wektora z oraz i, j iteruje po wszystkich elementach wektora.

Wtedy prawdopodobieństwo dla klasy c będzie wynosić:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

W wielomianowej regresji logistycznej zmienna wyjściowa może mieć więcej niż dwa możliwe wyjścia dyskretne . Rozważmy cyfrowy zbiór danych.

Wyjście:

Dokładność modelu regresji logistycznej (w%): 96,52294853963839

Jak ocenić model regresji logistycznej?

Możemy ocenić model regresji logistycznej, korzystając z następujących metryk:

• Dokładność: Dokładność podaje odsetek poprawnie sklasyfikowanych instancji.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Precyzja: Precyzja koncentruje się na trafności pozytywnych przewidywań.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Przywołanie (czułość lub prawdziwie dodatni współczynnik): Przypomnienie sobie czegoś mierzy odsetek prawidłowo przewidywanych pozytywnych przypadków wśród wszystkich rzeczywistych pozytywnych przypadków.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• Wynik F1: Wynik w F1 jest średnią harmoniczną precyzji i przypominania.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Obszar pod krzywą charakterystyki działania odbiornika (AUC-ROC): Krzywa ROC przedstawia odsetek prawdziwie dodatni w stosunku do współczynnika fałszywie dodatniego przy różnych progach. AUC-ROC mierzy pole pod tą krzywą, zapewniając zbiorczą miarę wydajności modelu w różnych progach klasyfikacji.
• Obszar pod krzywą przypomnienia o precyzji (AUC-PR): Podobny do AUC-ROC, AUC-PR mierzy obszar pod krzywą precyzji przypominania, zapewniając podsumowanie wydajności modelu przy różnych kompromisach w zakresie precyzji.

Kompromis w zakresie precyzji przywołania w przypadku ustawienia progu regresji logistycznej

Regresja logistyczna staje się techniką klasyfikacji dopiero wtedy, gdy uwzględni się próg decyzyjny. Ustalenie wartości progowej jest bardzo ważnym aspektem regresji logistycznej i zależy od samego problemu klasyfikacji.

Na decyzję o wartości wartości progowej duży wpływ mają wartości precyzja i pamięć. Idealnie byłoby, gdybyśmy chcieli zarówno precyzji, jak i zapamiętywania wynoszącej 1, ale rzadko tak się dzieje.

W przypadku A Kompromis precyzja-przypomnienie , do określenia progu używamy następujących argumentów:

1. Niska precyzja/wysokie przywołanie: W zastosowaniach, w których chcemy zmniejszyć liczbę fałszywie negatywnych wyników bez konieczności zmniejszania liczby fałszywie pozytywnych wyników, wybieramy wartość decyzyjną o niskiej wartości Precyzji lub wysokiej wartości Recall. Na przykład w przypadku aplikacji dotyczącej diagnozy raka nie chcemy, aby jakikolwiek pacjent dotknięty chorobą był klasyfikowany jako zdrowy, bez zwrócenia szczególnej uwagi na to, czy u pacjenta błędnie zdiagnozowano nowotwór. Dzieje się tak dlatego, że brak nowotworu można wykryć na podstawie dalszych chorób, natomiast u odrzuconego już kandydata nie można wykryć obecności choroby.
2. Wysoka precyzja/niskie przywołanie: W zastosowaniach, w których chcemy zmniejszyć liczbę fałszywych alarmów bez konieczności zmniejszania liczby fałszywych alarmów, wybieramy wartość decyzyjną, która ma wysoką wartość Precyzji lub niską wartość Recall. Przykładowo, jeśli klasyfikujemy klientów, czy zareagują pozytywnie czy negatywnie na spersonalizowaną reklamę, chcemy mieć absolutną pewność, że klient zareaguje pozytywnie na reklamę, gdyż w przeciwnym razie negatywna reakcja może spowodować utratę potencjalnej sprzedaży ze strony klienta. klient.

Różnice między regresją liniową i logistyczną

Różnica między regresją liniową a regresją logistyczną polega na tym, że wynik regresji liniowej jest wartością ciągłą, która może być dowolna, podczas gdy regresja logistyczna przewiduje prawdopodobieństwo, że instancja należy do danej klasy, czy nie.

Regresja logistyczna – często zadawane pytania (FAQ)

Czym jest regresja logistyczna w uczeniu maszynowym?

Regresja logistyczna to metoda statystyczna służąca do opracowywania modeli uczenia maszynowego z binarnymi zmiennymi zależnymi, czyli binarnymi. Regresja logistyczna to technika statystyczna stosowana do opisu danych i związku między jedną zmienną zależną a jedną lub większą liczbą zmiennych niezależnych.

Jakie są trzy rodzaje regresji logistycznej?

Regresję logistyczną dzieli się na trzy typy: binarną, wielomianową i porządkową. Różnią się wykonaniem i teorią. Regresja binarna dotyczy dwóch możliwych wyników: tak lub nie. Wielomianową regresję logistyczną stosuje się, gdy istnieją trzy lub więcej wartości.

Dlaczego do problemu klasyfikacji stosuje się regresję logistyczną?

Regresję logistyczną łatwiej jest wdrożyć, zinterpretować i wytrenować. Bardzo szybko klasyfikuje nieznane rekordy. Gdy zbiór danych można liniowo oddzielić, działa dobrze. Współczynniki modelu można interpretować jako wskaźniki ważności cech.

Co odróżnia regresję logistyczną od regresji liniowej?

Podczas gdy regresja liniowa służy do przewidywania ciągłych wyników, regresja logistyczna służy do przewidywania prawdopodobieństwa przypisania obserwacji do określonej kategorii. Regresja logistyczna wykorzystuje funkcję logistyczną w kształcie litery S do mapowania przewidywanych wartości w zakresie od 0 do 1.

Jaką rolę odgrywa funkcja logistyczna w regresji logistycznej?

Regresja logistyczna opiera się na funkcji logistycznej, która przekształca wynik na wynik prawdopodobieństwa. Wynik ten reprezentuje prawdopodobieństwo, że obserwacja należy do określonej klasy. Krzywa w kształcie litery S pomaga w progowaniu i kategoryzowaniu danych w postaci wyników binarnych.