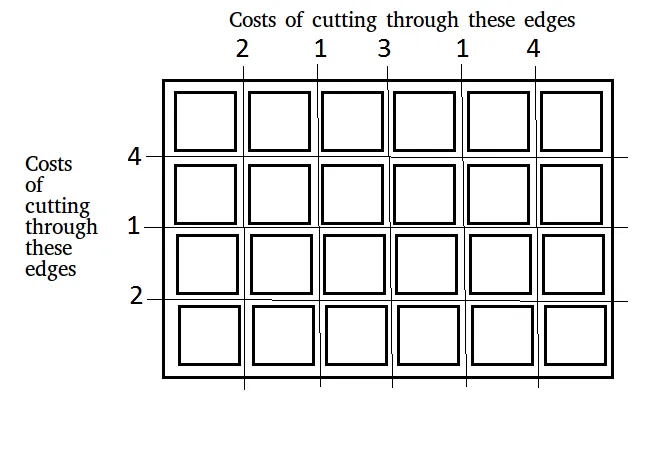
Biorąc pod uwagę tablicę wymiarów n × m który należy pociąć na n × m kwadratów. Koszt wykonania cięcia wzdłuż krawędzi poziomej lub pionowej podawany jest w dwóch tablicach:

• X[] : Cięcie kosztów wzdłuż pionowych krawędzi (wzdłuż).
• I[] : Cięcie kosztów wzdłuż krawędzi poziomych (wszerz).

Znajdź minimalny całkowity koszt wymagany do optymalnego pocięcia deski na kwadraty.

Przykłady: 

Wejście: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Wyjście: 42
Wyjaśnienie:

Początkowo nie. segmentów poziomych = 1 i nie. segmentów pionowych = 1.
Optymalny sposób cięcia na kwadrat to:
Wybierz 4 (od x) -> cięcie pionowe Koszt = 4 × segmenty poziome = 4
 Teraz segmenty poziome = 1 segmenty pionowe = 2.
Wybierz 4 (od y) -> cięcie poziome Koszt = 4 × segmenty pionowe = 8
 Teraz segmenty poziome = 2 segmenty pionowe = 2.
Wybierz 3 (od x) -> cięcie pionowe Koszt = 3 × segmenty poziome = 6
 Teraz segmenty poziome = 2 segmenty pionowe = 3.
Wybierz 2 (od x) -> cięcie pionowe Koszt = 2 × segmenty poziome = 4
 Teraz segmenty poziome = 2 segmenty pionowe = 4.
Wybierz 2 (od y) -> cięcie poziome Koszt = 2 × segmenty pionowe = 8
 Teraz segmenty poziome = 3 segmenty pionowe = 4.
Wybierz 1 (od x) -> cięcie pionowe Koszt = 1 × segmenty poziome = 3
Teraz segmenty poziome = 3 segmenty pionowe = 5.
Wybierz 1 (od x) -> cięcie pionowe Koszt = 1 × segmenty poziome = 3
Teraz segmenty poziome = 3 segmenty pionowe = 6.
Wybierz 1 (od y) -> cięcie poziome Koszt = 1 × segmenty pionowe = 6
Teraz segmenty poziome = 4 segmenty pionowe = 6.
Zatem całkowity koszt = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Wejście: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Wyjście: 15
Wyjaśnienie:
Początkowo nie. segmentów poziomych = 1 i nie. segmentów pionowych = 1.
Optymalny sposób cięcia na kwadrat to:
Wybierz 1 (od y) -> cięcie poziome Koszt = 1 × segmenty pionowe = 1
Teraz segmenty poziome = 2 segmenty pionowe = 1.
Wybierz 1 (od y) -> cięcie poziome Koszt = 1 × segmenty pionowe = 1
Teraz segmenty poziome = 3 segmenty pionowe = 1.
Wybierz 1 (od y) -> cięcie poziome Koszt = 1 × segmenty pionowe = 1
Teraz segmenty poziome = 4 segmenty pionowe = 1.
Wybierz 1 (od x) -> cięcie pionowe Koszt = 1 × segmenty poziome = 4
Teraz segmenty poziome = 4 segmenty pionowe = 2.
Wybierz 1 (od x) -> cięcie pionowe Koszt = 1 × segmenty poziome = 4
Teraz segmenty poziome = 4 segmenty pionowe = 3.
Wybierz 1 (od x) -> cięcie pionowe Koszt = 1 × segmenty poziome = 4
Teraz segmenty poziome = 4 segmenty pionowe = 4
Zatem całkowity koszt = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Spis treści

• [Podejście naiwne] Wypróbuj wszystkie permutacje - O((n+m)!×(n+m)) Czas i O(n+m) Przestrzeń
• [Oczekiwane podejście] Użycie techniki zachłannej - O( n (log n)+m (log m)) Czas i O(1) Przestrzeń

[Podejście naiwne] Wypróbuj wszystkie permutacje - O((n+m)!×(n+m)) Czas i O(n+m) Przestrzeń

Pomysł polega na wygenerowaniu wszystkich możliwych permutacji danych cięć, a następnie obliczeniu kosztu każdej permutacji. Na koniec zwróć wśród nich minimalny koszt.

Notatka: Podejście to nie jest możliwe w przypadku większych danych wejściowych, ponieważ liczba permutacji rośnie silniowo jako (m+n-2)!.
Dla każdej permutacji musimy obliczyć koszt w czasie O(m+n). Stąd całkowita złożoność czasowa wynosi O((m+n−2)!×(m+n)).

[Oczekiwane podejście] Użycie techniki zachłannej - O( n (log n)+m (log m)) Czas i O(1) Przestrzeń

Pomysł jest taki, aby najpierw wykonać najdroższe cięcia za pomocą chciwe podejście . Zaobserwowano, że wybór najwyższej obniżki kosztów na każdym etapie zmniejsza przyszłe koszty, wpływając na wiele elementów jednocześnie. Sortujemy koszty cięć pionowych (x) i poziomych (y) w kolejności malejącej, a następnie iteracyjnie wybieramy większy, aby zmaksymalizować oszczędności. Pozostałe kawałki są przetwarzane oddzielnie, aby zapewnić optymalne rozdzielenie wszystkich sekcji.

Co się stanie, gdy dokonamy cięcia?

• Cięcie poziome → przecinasz szerokość, więc zwiększa się liczba poziomych pasków (hCount++). Jednak koszt jest mnożony przez vCount (liczbę pionowych pasków), ponieważ poziome cięcie musi przejść przez wszystkie pionowe segmenty.
• Cięcie pionowe → przecinasz wysokość, więc liczba pionowych pasków wzrasta (vCount++). Ale koszt jest mnożony przez hCount (liczbę poziomych pasków), ponieważ pionowe cięcie musi przejść przez wszystkie poziome segmenty.

Kroki, aby rozwiązać problem:

• Sortuj tablice x i y w kolejności malejącej.
• Użyj dwóch wskaźników, jednego dla x i jednego dla y, zaczynając od największej wartości i kierując się w stronę mniejszych wartości.
• Utrzymuj hCount i vCount, aby śledzić, na ile segmentów wpływa każde cięcie, i odpowiednio je aktualizuj.
• Wykonuj iteracje, podczas gdy zarówno x, jak i y mają nieprzetworzone kawałki, zawsze wybierając większy koszt, aby zminimalizować ogólne wydatki.
• Jeśli x pozostały cięcia, przetwórz je za pomocą mnożnika hCount; podobnie przetwarzaj pozostałe cięcia za pomocą vCount.
• Zsumuj całkowity koszt na każdym etapie, korzystając ze wzoru: obniż koszt * liczba dotkniętych elementów, zapewniając minimalny koszt.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42