Moment bezwładności jest właściwością ciała znajdującego się w ruchu obrotowym. Moment bezwładności jest właściwością ciał obrotowych, która ma tendencję do przeciwstawiania się zmianom ruchu obrotowego ciała. Jest ona podobna do bezwładności dowolnego ciała w ruchu postępowym. Matematycznie moment bezwładności jest podawany jako suma iloczynu masy każdej cząstki i kwadratu odległości od osi obrotu. Mierzy się go w jednostce kgm 2 .
Przyjrzyjmy się szczegółowo momentowi bezwładności w poniższym artykule.
Spis treści
- Definicja momentu bezwładności
- Wzór na moment bezwładności
- Czynniki wpływające na moment bezwładności
- Jak obliczyć moment bezwładności?
- Wzór na moment bezwładności dla różnych kształtów
- Promień bezwładności
- Twierdzenia o momencie bezwładności
- Momenty bezwładności dla różnych obiektów
Definicja momentu bezwładności
Moment bezwładności to tendencja ciała w ruchu obrotowym, która przeciwdziała zmianie jego ruchu ruch obrotowy wskutek sił zewnętrznych. Moment bezwładności zachowuje się jak masa kątowa i nazywany jest bezwładnością obrotową. Moment bezwładności jest analogiczny do mechanicznego Bezwładność cielesny.
MOI definiuje się jako ilość wyrażoną jako suma iloczynu masa każdej cząstki z kwadratem jej odległości od osi obrotu dla dowolnej cząstki wykonującej ruch obrotowy.
Jednostka momentu bezwładności
Moment bezwładności jest wielkością skalarną, a jednostką SI momentu bezwładności jest kgm 2 .
Wzór wymiarowy momentu bezwładności
Ponieważ moment bezwładności jest podawany jako iloczyn masy i kwadratu odległości. Jego formuła wymiarowa jest obliczany jako iloczyn wzoru wymiarowego masy i kwadratu wzoru wymiarowego długości. Wzór wymiarowy momentu bezwładności to: ML 2
Co to jest bezwładność?
Bezwładność jest właściwością materii, dzięki której ma ona tendencję do przeciwstawiania się zmianie stanu swego ruchu. Oznacza to, że ciało w spoczynku stara się pozostać w spoczynku i opierać się wszelkim siłom próbującym wprawić je w ruch, natomiast ciało w ruchu stara się kontynuować ruch i stawić opór każdej sile próbującej zmienić wielkość jego ruchu. Pod względem ilościowym jest ona równa maksymalnej sile próbującej zmienić swój stan ruch .
Dowiedz się więcej o Bezwładność .
Wzór na moment bezwładności
Moment bezwładności wynosi a ilość skalarna . Matematycznie iloczyn kwadratu masy cząstki i odległości od osi obrotu nazywany jest momentem bezwładności cząstki względem osi obrotu.
Ogólny wzór na znalezienie momentu bezwładności dowolnego obiektu to:
ja = pan 2
Gdzie,
M jest masą obiektu”
R jest odległością od osi obrotu
W przypadku ciała składającego się z ciągłych, nieskończenie małych cząstek, do obliczenia momentu bezwładności stosuje się całkową postać momentu bezwładności.
ja = ∫dI
ja =
int_{0}^{M} r^2 dm
Moment bezwładności układu cząstek
Moment bezwładności układu cząstek wyraża się wzorem:
ja = ∑m I R I 2
Gdzie,
R I jest prostopadłą odległością itcząstka od osi
M I jest masą itcząstka
Powyższe równanie momentu bezwładności mówi, że moment bezwładności układu cząstek jest równy sumie iloczynu masy każdej cząstki i kwadratu odległości od osi obrotu każdej cząstki.
Dla rysunku podanego poniżej
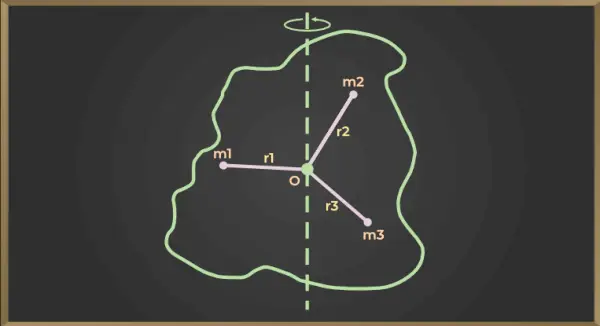
Moment bezwładności pierwszej cząstki = m1× r12
Moment bezwładności drugiej cząstki = m2× r22
Moment bezwładności trzeciej cząstki = m3×r32
Podobnie,
Moment bezwładności ntcząstka = mN×rN2
Teraz moment bezwładności całego ciała względem osi obrotu AB będzie równy sumie momentów bezwładności wszystkich cząstek, tj
ja = m1×r12+ m2× r22+ m3× r32+……+mN×rN2
stany w usa
Ja = Σm I × r I 2
Gdzie,
I reprezentują moment bezwładności ciała względem osi obrotu
M I jest masą itcząstka,
R I jest promieniem itcząstka
S reprezentuje sumę.
Z równania można powiedzieć, że moment bezwładności ciała względem ustalonej osi jest równy sumie iloczynu masy każdej cząstki tego ciała i kwadratu jego prostopadłej odległości od ustalonej osi.
Czynniki wpływające na moment bezwładności
Moment bezwładności dowolnego obiektu zależy od następujących wartości:
- Kształt i wielkość obiektu
- Gęstość materiału obiektu
- Oś obrotu
Jak obliczyć moment bezwładności?
Przyzwyczaja się do tego kilka sposobów obliczyć moment bezwładności dowolnego obracającego się obiektu.
- W przypadku obiektów jednorodnych moment bezwładności oblicza się, biorąc iloczyn ich masy przez kwadrat odległości od osi obrotu (r2).
- W przypadku obiektów niejednorodnych moment bezwładności obliczamy, sumując iloczyn mas poszczególnych punktów przy każdym innym promieniu, w tym celu stosuje się wzór:
ja = ∑m I R I 2
Wzór na moment bezwładności dla różnych kształtów
W poniższej tabeli omówiono wyrażenia momentu bezwładności niektórych obiektów symetrycznych wraz z ich osią obrotu:

| Obiekt | Oś | Wyrażenie momentu bezwładności |
|---|---|---|
| Cylinder pusty, cienkościenny | Centralny | Ja = Pan2 |
| Cienki pierścień | Średnica | Ja = 1/2 pana2 |
| Pierścień pierścieniowy lub pusty cylinder | Centralny | Ja = 1/2 M(r22+ r12) |
| Solidny cylinder | Centralny | Ja = 1/2 pana2 |
| Jednolity dysk | Średnica | Ja = 1/4 Pana2 |
| Pusta Kula | Centralny | Ja = 2/3 Pana2 |
| Solidna kula | Centralny | Ja = 2/5 Pan2 |
| Jednolita symetryczna powłoka sferyczna | Centralny | |
| Płyta jednolita lub prostokątna równoległościan | Centralny | Ja = 1/12 M(a2+ b2) |
| Cienki pręt | Centralny | Ja = 1/12 Pan2 |
| Cienki pręt | Na końcu pręta | Ja = 1/3 pana2 |
Promień bezwładności
The Promień bezwładności ciała definiuje się jako prostopadłą odległość od osi obrotu do punktu masy, którego masa jest równa masie całego ciała, a moment bezwładności jest równy rzeczywistemu momentowi bezwładności obiektu założono, że w tym miejscu skupia się całkowita masa ciała. To wyimaginowana odległość. Promień bezwładności jest oznaczony przez K.
Jeżeli masa i promień bezwładności ciała wynoszą odpowiednio M i K, to moment bezwładności ciała wynosi
Ja = MK 2 ……(1)
Zatem promień bezwładności ciała jest prostopadły do osi obrotu, której kwadrat pomnożony przez masę tego ciała daje moment bezwładności tego ciała względem tej osi.
Ponownie za pomocą równania (1) K2= Ja/M
K = √(I/m)
Zatem promień obrotu ciała wokół osi jest równy pierwiastkowi kwadratowemu stosunku ciała wokół tej osi.
Twierdzenia o momencie bezwładności
Istnieją dwa rodzaje twierdzeń, które są bardzo ważne w odniesieniu do momentu bezwładności:
- Twierdzenie o osi równoległej
- Twierdzenie o osi prostopadłej
Twierdzenie o osi prostopadłej
Twierdzenie o osi prostopadłej stwierdza, że suma momentu bezwładności ciała względem dwóch wzajemnie prostopadłych osi znajdujących się w płaszczyźnie ciała jest równa momentowi bezwładności ciała względem trzeciej osi, która jest prostopadła do obu osi i przechodzi przez ich punkt skrzyżowania.

Na powyższym rysunku WÓŁ I SP. Z O.O to dwie osie w płaszczyźnie ciała, które są do siebie prostopadłe. Trzecia oś to OZ która jest prostopadła do płaszczyzny ciała i przechodzi przez punkt przecięcia WÓŁ I SP. Z O.O osie. Jeśli I X , I I , I I z są momentami bezwładności ciała względem osi WÓŁ , SP. Z O.O , I OZ odpowiednio osi, to zgodnie z tym twierdzeniem
I X + ja I = ja z
Twierdzenie o osi równoległej
Według Twierdzenie o osi równoległej , moment bezwładności ciała względem danej osi jest sumą momentu bezwładności względem osi przechodzącej przez środek masy tego ciała i iloczynu kwadratu masy ciała i prostopadłej odległości między dwie osie.

Niech na powyższym rysunku musimy znaleźć moment bezwładności I O ciała przechodzącego przez ten punkt O oraz wokół osi prostopadłej do płaszczyzny, natomiast moment bezwładności ciała przechodzącego przez środek masy C i wokół osi równoległej do danej osi I C , to zgodnie z tym twierdzeniem
I O = ja C + Mł 2
Gdzie
M jest masą całego ciała
l jest prostopadłą odległością pomiędzy dwiema osiami.
Momenty bezwładności dla różnych obiektów
Moment bezwładności różnych obiektów omówiono poniżej w tym artykule
Moment bezwładności płyty prostokątnej
Jeżeli masa płyty wynosi M, długość l i szerokość b, to moment bezwładności przechodzi przez środek ciężkości i wokół osi prostopadłej do płaszczyzny płyty.
czytaj pliki json

ja = M(l 2 + b 2 / 12)
Moment bezwładności dysku
Jeżeli dysk ma masę M i promień r, to moment bezwładności względem osi geometrycznej dysku wynosi:

Ja = 1/2 (pan 2 )
Moment bezwładności pręta
Jeżeli masa pręta wynosi M, a długość l, to moment bezwładności względem osi prostopadłej do długości pręta i przechodzącej przez jego środek ciężkości

Ja = ML 2 /12
Moment bezwładności okręgu
Jeżeli masa pierścienia wynosi M, a promień pierścienia wynosi r, to moment bezwładności względem osi przechodzącej prostopadle do środka pierścienia wynosi

Ja = Pan 2
Moment bezwładności kuli
Jeżeli stała kula ma masę M i promień r, wówczas moment bezwładności względem jej średnicy wynosi

Ja = 2/5 Pan 2
Moment bezwładności stałego cylindra
Moment bezwładności pełnego cylindra o promieniu „R” i masie M jest określony wzorem

Ja = 1/2MR 2
Moment bezwładności pustego cylindra
Wydrążony cylinder ma dwa promienie, mianowicie promień wewnętrzny i promień zewnętrzny. Moment bezwładności pustego cylindra o masie M i promieniu zewnętrznym R1i promień wewnętrzny R2podaje się jako

Ja = 1/2M(R 1 2 + R 2 2 )
Moment bezwładności kuli stałej
Moment bezwładności stałej kuli o masie „M” i promieniu „R” podaje się jako:

Ja = 2/5MR 2
Moment bezwładności pustej kuli
Moment bezwładności pustej kuli o masie M i promieniu „R” podaje się jako:

Ja = 2/3MR 2
Moment bezwładności pierścienia
Moment bezwładności pierścienia jest podany dla dwóch przypadków, gdy oś obrotu przechodzi przez środek i gdy oś obrotu przechodzi przez średnicę.
Moment bezwładności pierścienia względem osi przechodzącej przez środek jest określony przez
przekonwertuj ciąg na int

Ja = Pan 2
Moment bezwładności pierścienia względem osi przechodzącej przez średnicę jest określony przez

Ja = Pan 2 /2
Moment bezwładności kwadratu
Moment bezwładności kwadratu boku „a” jest określony jako

ja = a 4 /12
Moment bezwładności kwadratowej płyty o boku długości „l” i masie M jest podany jako:
Ja = 1/6 ml 2
Moment bezwładności trójkąta
Moment bezwładności trójkąta jest podawany dla 3 sytuacji: pierwsza, gdy oś przechodzi przez środek, druga, gdy oś przechodzi przez podstawę i trzecia, gdy oś jest prostopadła do podstawy. Zobaczmy przepis na nie jeden po drugim. Dla trójkąta o podstawie „b” i wysokości „h” wzór na moment bezwładności podaje się w następujący sposób

Kiedy oś przechodzi przez Centroid
ja = bh 3 /36
Kiedy oś przechodzi przez podstawę
ja = bh 3 /12
Gdy oś jest prostopadła do podstawy
Ja = (hb/36)(ur 2 - B 1 b + b 1 2 )
Różnica między momentem bezwładności a bezwładnością
Różnicę między bezwładnością a momentem bezwładności przedstawiono w tabeli poniżej:
| Tak nie. | Bezwładność | Moment bezwładności |
|---|---|---|
| 1. | Jego znaczenie jest w ruchu liniowym. | Jego znaczenie jest w ruchu obrotowym. |
| 2. | Jest to właściwość obiektu, która przeciwstawia się zmianie stanu obiektu w ruchu liniowym. | Moment bezwładności to właściwość obiektu, która przeciwdziała zmianie stanu obiektu w ruchu obrotowym. |
| 3. | Bezwładność obiektu zależy tylko od jego masy. | Moment bezwładności obiektu zależy od jego masy i rozkładu masy względem osi obrotu. |
| 4. | Bezwładność obiektu jest stała. | Moment bezwładności obiektu zmienia się w zależności od osi obrotu. |
Energia kinetyczna wirującego ciała
Załóżmy, że ciało o masie „m” obraca się z prędkością v w odległości „r” od osi obrotu. Jego prędkość kątową wyraża się wówczas wzorem ω = v/r, a następnie v = rω. Teraz wiemy, że Energia kinetyczna ciała jest dane przez
KE = 1/2mV 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Oh2
⇒ KE = 1/2Iω 2
Stąd energia kinetyczna wirującego ciała jest równa połowie iloczynu momentu bezwładności i prędkość kątowa cielesny. Nazywa się także energią kinetyczną obracającego się ciała Obrotowa energia kinetyczna . Wzór na obrotową energię kinetyczną podano jako
KE = 1/2Iω 2
Moment bezwładności (I) jest niezależny od prędkości kątowej ciała. Jest to funkcja masy obracającego się ciała i odległości tego ciała od osi obrotu. Dlatego obserwujemy, że ruch kątowy jest analogiczny do ruchu liniowego, co oznacza, że znaczenie momentu bezwładności polega na tym, że daje on wyobrażenie o tym, jak masy są rozłożone w różnych odległościach od osi obrotu w obracającym się ciele.
Zastosowanie momentu bezwładności
Moment bezwładności ma różne zastosowania, niektóre z nich omówiono poniżej:
- Ze względu na większy moment bezwładności Ziemia obraca się wokół własnej osi z tą samą prędkością kątową.
- Pod silnikiem do zabawy dla dzieci umieszczono małe ruchome koło. Po otarciu tego koła o podłoże i opuszczeniu silnika, na skutek momentu bezwładności koła, silnik jeszcze przez jakiś czas pracuje.
- Każdy silnik składa się z dużego i ciężkiego koła przymocowanego do wału, którego większość masy znajduje się na jego obwodzie. Dlatego jego moment bezwładności jest duży. To koło nazywa się kołem zamachowym. Moment obrotowy napędzający wał silnika stale rośnie. Dlatego obrót wału może nie być równomierny, ale ze względu na obecność ruchomego koła o większej bezwładności, wał nadal obraca się z prawie stałą prędkością.
- W kole wozów z bykami, rikszami, hulajnogami, rowerami itp. większość masy skupia się na jego kole lub obręczy. ta obręcz lub rutyna jest przymocowana do osi koła za pomocą sztywnych szprych. W ten sposób zwiększa się jego moment bezwładności. Dlatego też, gdy nogi przestają się poruszać podczas jazdy na rowerze, koło nadal się kręci przez pewien czas.
Sprawdź także
- Kinematyka ruchu obrotowego
- Ruch ciała sztywnego
- Ruch toczny
Rozwiązane przykłady momentów bezwładności
Przykład 1: Ciało o masie 500 g obraca się wokół osi. odległość środka masy ciała od osi obrotu wynosi 1,2 m. znajdź moment bezwładności ciała względem osi obrotu.
Rozwiązanie:
Biorąc pod uwagę, że M = 500 g = 0,5 kg, r = 1,2 m.
Można oczywiście założyć, że cała masa ciała znajduje się w jego środku masy. Następnie moment bezwładności ciała względem osi obrotu.
Ja = Pan2
Ja = 0,5 × (1,2)2
Ja = 0,72 kg m2
Przykład 2: Promień obrotu wokół osi oddalonej o 12 cm od środka masy ciała o masie 1,2 kg wynosi 13 cm. Oblicz promień obrotu i moment bezwładności względem osi przechodzącej przez środek masy.
Rozwiązanie:
Biorąc pod uwagę, że M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, jaCM=?
Z twierdzenia o osi równoległej I = ICM+ Mł2
K2= KCM2+ l2
.tostring Javalub KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Teraz moment bezwładności ICM= MKCM2
ICM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Przykład 3: Ciało o masie 0,1 kg obraca się wokół osi. jeżeli odległość środka masy ciała od osi obrotu wynosi 0,5 m, to znajdź moment bezwładności ciała.
Rozwiązanie:
Biorąc to pod uwagę, M = 0,1 kg i r = 0,5 m
więc ja = pan2
Ja = 0,1 × (0,5)2
I = 0,025 kg m2
Przykład 4: Moment bezwładności pierścieni względem osi przechodzącej przez jego środek prostopadłej do płaszczyzny pierścienia kołowego wynosi 200 gm·cm 2 . Jaki będzie moment bezwładności względem jego średnicy?
Rozwiązanie:
Moment bezwładności pierścienia kołowego względem osi przechodzącej przez inny środek prostopadły do jego płaszczyzny
PAN2= 200 gramów cm2
Moment bezwładności zbliżony do średnicy
= 1/2 MR2
= 1/2 × 200 = 100 gramów cm2
Często zadawane pytania dotyczące momentów bezwładności
Jak obliczyć moment bezwładności?
Podstawowy wzór na znalezienie momentu bezwładności dowolnego jednolitego obiektu to:
ja = pan 2
Gdzie,
M jest masą obiektu”
R jest odległością od osi obrotu
Jak obliczyć moment bezwładności belki?
Moment bezwładności belki wzdłuż środka i osi poziomej do niej oblicza się ze wzoru:
Ja = ML 2 / 12
Od czego zależy moment bezwładności ciała?
Moment bezwładności dowolnego obiektu zależy od czynników podanych poniżej:
- Masa Ciała,
- Oś obrotu
- Kształt i wielkość obiektu
Jaka jest jednostka momentu bezwładności?
Jednostką momentu bezwładności jest Kgm 2
Czy moment bezwładności może być ujemny?
Nie, moment bezwładności nigdy nie może być ujemny.
Co to jest masowy moment bezwładności?
Masowy moment bezwładności jest miarą oporu ciała na zmianę jego pędu lub kierunku kątowego. Masowy moment bezwładności masy punktowej wyraża się wzorem I = mr2a dla układu cząstek masowy moment bezwładności podaje się jako I = ΣIMIRI2
Co to jest obszarowy moment bezwładności?
Powierzchniowy moment bezwładności jest właściwością płaszczyzny kształtu 2D, która pokazuje, w jaki sposób punkty są rozproszone względem dowolnej osi w płaszczyźnie. Powierzchniowy moment bezwładności jest również znany jako drugi moment powierzchniowy lub kwadratowy moment powierzchniowy. Wzór na moment bezwładności powierzchniowej w płaszczyźnie xy podano jako Ixy= ∫xy dxdxy = ∫xy dA
