W informatyce istnieją pewne problemy, których rozwiązania nie znaleziono jeszcze, problemy są podzielone na klasy zwane Klasy złożoności . W teorii złożoności klasa złożoności to zbiór problemów o powiązanej złożoności. Zajęcia te pomagają naukowcom grupować problemy na podstawie ilości czasu i miejsca potrzebnego do rozwiązania problemów oraz weryfikacji rozwiązań. Jest to gałąź teorii obliczeń zajmująca się zasobami wymaganymi do rozwiązania problemu.
menu JavaScript
Wspólnymi zasobami są czas i przestrzeń, co oznacza, ile czasu zajmuje algorytmowi rozwiązanie problemu i odpowiadające mu zużycie pamięci.
- Złożoność czasowa algorytmu służy do opisania liczby kroków wymaganych do rozwiązania problemu, ale może być również wykorzystana do opisania czasu potrzebnego na weryfikację odpowiedzi.
- Złożoność przestrzenna algorytmu opisuje ilość pamięci wymaganej do działania algorytmu.
Klasy złożoności są przydatne w organizowaniu podobnych typów problemów.
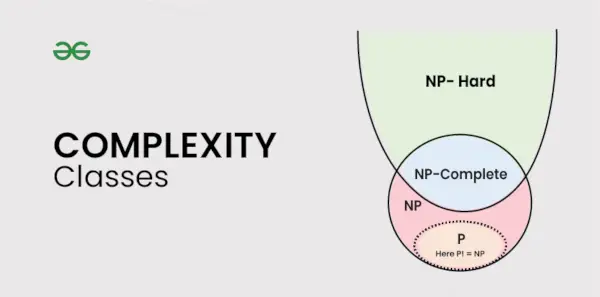
Rodzaje klas złożoności
W tym artykule omówiono następujące klasy złożoności:
- Klasa P
- Klasa NP
- Klasa CoNP
- NP-twardy
- NP-kompletny
Klasa P
Litera P w klasie P oznacza Czas wielomianowy. Jest to zbiór problemów decyzyjnych (problemów z odpowiedzią tak lub nie), które mogą być rozwiązane przez maszynę deterministyczną w czasie wielomianowym.
Cechy:
- Rozwiązanie Problem P s jest łatwe do znalezienia.
- P jest często klasą problemów obliczeniowych, które można rozwiązać i rozwiązać. Przejezdny oznacza, że problemy można rozwiązać zarówno w teorii, jak i w praktyce. Jednak problemy, które można rozwiązać w teorii, ale nie w praktyce, są znane jako nierozwiązywalne.
Ta klasa zawiera wiele problemów:
- Obliczanie największego wspólnego dzielnika.
- Znalezienie maksymalnego dopasowania.
- Sortowanie przez scalanie
Klasa NP
NP w klasie NP oznacza Niedeterministyczny czas wielomianowy . Jest to zbiór problemów decyzyjnych, które można rozwiązać za pomocą maszyny niedeterministycznej w czasie wielomianowym.
Cechy:
- Rozwiązania klasy NP są trudne do znalezienia, ponieważ są rozwiązywane przez maszynę niedeterministyczną, ale rozwiązania są łatwe do sprawdzenia.
- Problemy NP można zweryfikować za pomocą maszyny Turinga w czasie wielomianowym.
Przykład:
Rozważmy przykład, aby lepiej zrozumieć klasa NP . Załóżmy, że istnieje firma posiadająca łącznie 1000 pracownicy posiadający unikalnego pracownika identyfikatory . Załóżmy, że istnieją 200 dla nich dostępne pokoje. Wybór 200 pracownicy muszą być połączeni w pary, ale dyrektor generalny firmy ma dane niektórych pracowników, którzy ze względów osobistych nie mogą pracować w tym samym pomieszczeniu.
To jest przykład NP problem. Ponieważ łatwo jest sprawdzić, czy dany wybór 200 pracownicy zaproponowani przez współpracownika są zadowalający czy nie, tzn. na liście podanej przez Prezesa nie pojawia się żadna para wzięta z listy współpracowników. Jednak wygenerowanie takiej listy od zera wydaje się tak trudne, że jest całkowicie niepraktyczne.
Oznacza to, że jeśli ktoś może podać nam rozwiązanie problemu, możemy znaleźć poprawną i niepoprawną parę w czasie wielomianowym. Zatem dla NP klasowym, możliwa jest odpowiedź, którą można obliczyć w czasie wielomianowym.
dziedziczenie Javy
Klasa ta zawiera wiele problemów, które chciałoby się skutecznie rozwiązać:
- Problem spełnialności logicznej (SAT).
- Problem ścieżki Hamiltona.
- Kolorowanie wykresu.
Klasa Co-NP
Co-NP oznacza uzupełnienie klasy NP. Oznacza to, że jeśli odpowiedź na problem w Co-NP brzmi „Nie”, to istnieje dowód, który można sprawdzić w czasie wielomianowym.
Cechy:
- Jeśli problem X znajduje się w NP, to jego uzupełnienie X’ również znajduje się w CoNP.
- W przypadku problemu NP i CoNP nie ma potrzeby sprawdzania wszystkich odpowiedzi na raz w czasie wielomianowym, istnieje potrzeba weryfikacji tylko jednej konkretnej odpowiedzi tak lub nie w czasie wielomianowym, aby problem był w NP lub CoNP.
Oto kilka przykładowych problemów dla CoNP:
- Aby sprawdzić liczbę pierwszą.
- Faktoryzacja liczb całkowitych.
Klasa NP-trudna
Problem NP-trudny jest co najmniej tak trudny, jak najtrudniejszy problem w NP i jest to klasa problemów, w których każdy problem w NP redukuje się do NP-trudnego.
Cechy:
bash sprawdza, czy zmienna środowiskowa jest ustawiona
- Wszystkie problemy NP-trudne nie występują w NP.
- Ich sprawdzanie zajmuje dużo czasu. Oznacza to, że jeśli podane jest rozwiązanie problemu NP-trudnego, sprawdzenie, czy jest ono prawidłowe, zajmuje dużo czasu.
- Problem A jest NP-trudny, jeśli dla każdego problemu L w NP istnieje wielomianowa redukcja w czasie od L do A.
Oto niektóre przykłady problemów w Np-hard:
- Problem z zatrzymaniem.
- Kwalifikowane formuły logiczne.
- Brak cyklu Hamiltona.
Klasa NP-zupełna
Problem jest NP-zupełny, jeśli jest jednocześnie NP i NP-trudny. Problemy NP-zupełne są problemami trudnymi w NP.
Cechy:
- Problemy NP-zupełne są szczególne, ponieważ każdy problem klasy NP można przekształcić lub zredukować do problemów NP-zupełnych w czasie wielomianowym.
- Jeśli można rozwiązać problem NP-zupełny w czasie wielomianowym, to można również rozwiązać dowolny problem NP w czasie wielomianowym.
Oto niektóre przykładowe problemy:
- Cykl Hamiltona.
- Satysfakcja.
- Osłona wierzchołkowa .
| Klasa złożoności | Cecha charakterystyczna |
| P | Łatwo rozwiązać w czasie wielomianowym. |
| NP | Tak, odpowiedzi można sprawdzić w czasie wielomianowym. |
| Co-NP | Nie, odpowiedzi można sprawdzić w czasie wielomianowym. |
| NP-twardy | Wszystkie problemy NP-trudne nie występują w NP i ich sprawdzanie zajmuje dużo czasu. |
| NP-kompletny | Problem NP i NP-trudny jest NP-zupełny. |
