Co to jest cykl Hamiltona?
Cykl lub obwód Hamiltona na wykresie G jest cyklem, który odwiedza każdy wierzchołek G dokładnie raz i powraca do wierzchołka początkowego.
- Jeśli graf zawiera cykl Hamiltona, nazywa się go Wykres Hamiltona inaczej jest nieHamiltonowski .
- Znalezienie cyklu Hamiltona na wykresie jest dobrze znane Problem NP-zupełny , co oznacza, że nie ma znanego skutecznego algorytmu, który rozwiązałby go dla wszystkich typów grafów. Można to jednak rozwiązać w przypadku małych lub określonych typów wykresów.
Problem cyklu Hamiltona ma praktyczne zastosowania w różnych dziedzinach, takich jak logistyka, projektowanie sieci i informatyka .
Co to jest ścieżka Hamiltona?
Ścieżka Hamiltona na wykresie G jest ścieżką, która odwiedza każdy wierzchołek G dokładnie raz i Ścieżka Hamiltona nie musi wracać do wierzchołka początkowego. To otwarta ścieżka.
- Podobny do Cykl Hamiltona problem ze znalezieniem Ścieżka Hamiltona na ogólnym wykresie jest również NP-kompletny i może być wyzwaniem. Jednak często jest to łatwiejszy problem niż znalezienie cyklu Hamiltona.
- Ścieżki Hamiltona mają zastosowania w różnych dziedzinach, takich jak znajdowanie optymalnych tras w sieciach transportowych, projektowanie obwodów i badania nad teorią grafów .
Oświadczenie o problemach: Mając graf nieskierowany, zadaniem jest określenie, czy graf zawiera cykl Hamiltona, czy nie. Jeśli zawiera, drukuje ścieżkę.
Przykład:
Zalecane: Proszę o rozwiązanie ĆWICZYĆ najpierw, zanim przejdziemy do rozwiązania.Wejście: wykres[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1},{0, 1, 1, 1, 0}}
Wykres wejściowy[][]
0,06 jako ułamekWyjście: {0, 1, 2, 4, 3, 0}.
Wejście: wykres[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0},{0, 1, 1, 0, 0}}
Wykres wejściowy[][]
Wyjście: Rozwiązanie nie istnieje
Naiwny algorytm : Ten problem można rozwiązać, korzystając z poniższego pomysłu:
Wygeneruj wszystkie możliwe konfiguracje wierzchołków i wydrukuj konfigurację spełniającą podane ograniczenia. Będzie n! (n silni) konfiguracji. Zatem ogólna złożoność czasowa tego podejścia będzie wynosić NA!).
Cykl Hamiltona za pomocą Algorytm cofania :
Utwórz pustą tablicę ścieżek i dodaj wierzchołek 0 do tego. Dodaj kolejne wierzchołki, zaczynając od wierzchołka 1 . Przed dodaniem wierzchołka sprawdź, czy przylega on do wcześniej dodanego wierzchołka i czy nie został już dodany. Jeśli znajdziemy taki wierzchołek, dodajemy go jako część rozwiązania. Jeżeli nie znajdziemy wierzchołka to wracamy FAŁSZ .
Ilustracje:
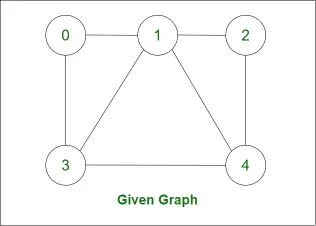
Znajdźmy cykl Hamiltona dla następującego wykresu:
- Zacznij od węzła 0.
- Zastosuj DFS do znalezienia ścieżki Hamiltona.
- Kiedy przypadek podstawowy osiągnie (tj. całkowita liczba przebytych węzłów == V (całkowity wierzchołek) ):
- Sprawdź, czy bieżący węzeł jest sąsiadem węzła początkowego.
- Jako węzeł 2 i węzeł 0 nie są sąsiadami więc odwróćcie się od tego.
Zaczynając od węzła początkowego 0 wywołującego DFS
- Ponieważ nie znaleziono cyklu na ścieżce {0, 3, 1, 4, 2}. Zatem wróć z węzła 2, węzła 4.
- Teraz zbadaj inną opcję dla węzła 1 (tj. węzła 2)
- Kiedy ponownie osiągnie warunek podstawowy, sprawdź cykl Hamiltona
- Ponieważ węzeł 4 nie jest sąsiadem węzła 0, ponownie nie znaleziono cyklu i należy powrócić.
- Powrót z węzła 4, węzła 2, węzła 1.
- Teraz przejrzyj inne opcje dla węzła 3.
Cykl Hamiltona
- Na ścieżce Hamiltona {0,3,4,2,1,0} otrzymujemy cykl, ponieważ węzeł 1 jest sąsiadem węzła 0.
- Wydrukuj więc tę ścieżkę cykliczną.
- To jest nasz cykl Hamiltona.
Poniżej znajduje się implementacja Backtracking do znajdowania cyklu Hamiltona:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Jawa /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Pyton # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> JavaScript >
PHP // PHP program for solution of // Hamiltonian Cycle problem // using backtracking $V = 5; /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ function isSafe($v, $graph, &$path, $pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if ($graph[$path[$pos - 1]][$v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for ($i = 0; $i < $pos; $i++) if ($path[$i] == $v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ function hamCycleUtil($graph, &$path, $pos) { global $V; /* base case: If all vertices are included in Hamiltonian Cycle */ if ($pos == $V) { // And if there is an edge from the // last included vertex to the first vertex if ($graph[$path[$pos - 1]][$path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point hamCycle() for ($v = 1; $v < $V; $v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe($v, $graph, $path, $pos)) { $path[$pos] = $v; /* recur to construct rest of the path */ if (hamCycleUtil($graph, $path, $pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ $path[$pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ function hamCycle($graph) { global $V; $path = array_fill(0, $V, 0); for ($i = 0; $i < $V; $i++) $path[$i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ $path[0] = 0; if (hamCycleUtil($graph, $path, 1) == false) { echo('
Solution does not exist'); return 0; } printSolution($path); return 1; } /* A utility function to print solution */ function printSolution($path) { global $V; echo('Solution Exists: Following is '. 'one Hamiltonian Cycle
'); for ($i = 0; $i < $V; $i++) echo(' '.$path[$i].' '); // Let us print the first vertex again to show the // complete cycle echo(' '.$path[0].'
'); } // Driver Code /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ $graph1 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 1), array(0, 1, 1, 1, 0), ); // Print the solution hamCycle($graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ $graph2 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 0), array(0, 1, 1, 0, 0)); // Print the solution hamCycle($graph2); // This code is contributed by mits ?>> Wyjście
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist>
Złożoność czasowa: O(N!), gdzie N jest liczbą wierzchołków.
Przestrzeń pomocnicza: O(1), ponieważ nie wykorzystuje się dodatkowej przestrzeni.
Notatka: Powyższy kod zawsze wypisuje cykl rozpoczynający się od 0 . Punkt początkowy nie powinien mieć znaczenia, ponieważ cykl można rozpocząć w dowolnym miejscu. Jeśli chcesz zmienić punkt początkowy, powinieneś dokonać dwóch zmian w powyższym kodzie.
Zmień ścieżkę [0] = 0; Do ścieżka[0] = s ; Gdzie S jest twój nowy punkt wyjścia . Zmień także pętlę for (int v = 1; v