Biorąc pod uwagę liczbę całkowitą N zadaniem jest znaleźć wszystko odrębne rozwiązania do problem n-królowych Gdzie N królowe są umieszczone na n * n szachownicy w taki sposób, aby żadne dwie królowe nie mogły się atakować.
Notatka: Każde rozwiązanie to unikalna konfiguracja N królowe reprezentowane jako permutacja [123....n] . Numer pod adresem I t pozycja wskazuje rząd królowej w I t kolumna. Na przykład [3142] pokazuje jeden taki układ.
Przykład:
Wejście: n = 4
Wyjście: [2 4 1 3] [3 1 4 2]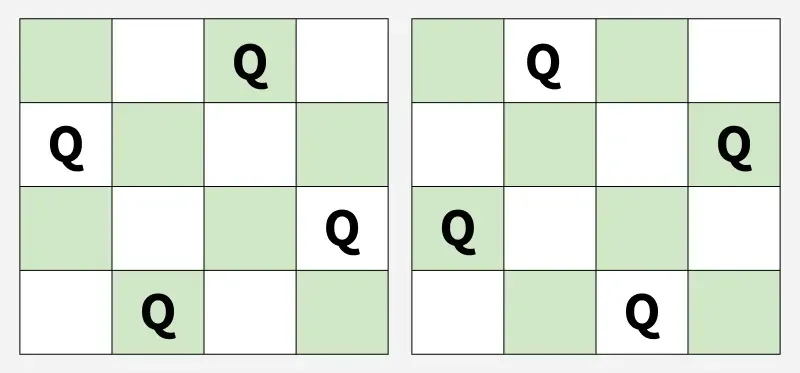
Wyjaśnienie : Oto 2 możliwe rozwiązania.Wejście: n = 2
Wyjście: []
Wyjaśnienie: Nie ma rozwiązania, gdyż królowe mogą atakować się nawzajem we wszystkich możliwych konfiguracjach.
Spis treści
- [Podejście naiwne] Generując wszystkie permutacje za pomocą rekurencji
- [Oczekiwane podejście] Korzystanie z cofania się i przycinania
- [Podejście alternatywne] Wycofywanie się przy użyciu maskowania bitów
[Podejście naiwne] - Stosowanie rekurencji - O(n! * n) czasu i O(n) przestrzeni
Prosty pomysł na rozwiązanie Problem z N-Queens polega na wygenerowaniu wszystkich możliwych permutacji [1 2 3 ... n] a następnie sprawdź, czy reprezentuje prawidłową konfigurację N-Queens. Ponieważ każda królowa musi znajdować się w innym rzędzie i kolumnie automatycznie używając permutacji dba o te zasady. Ale nadal musimy sprawdzić, czy na stole nie ma dwóch królowych ta sama przekątna.
Poniżej podano realizacja:
C++//C++ program to find all solution of N queen problem //using recursion #include
//Java program to find all solution of N queen problem //using recursion import java.util.ArrayList; class GfG { // Check if placement is safe static boolean isSafe(ArrayList<Integer> board int currRow int currCol) { for(int i = 0; i < board.size(); i++) { int placedRow = board.get(i); int placedCol = i + 1; // Check diagonals if(Math.abs(placedRow - currRow) == Math.abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve static void nQueenUtil(int col int n ArrayList<Integer> board ArrayList<ArrayList<Integer>> res boolean[] visited) { // If all queens placed add to res if(col > n) { res.add(new ArrayList<>(board)); return; } // Try each row in column for(int row = 1; row <= n; row++) { // If row not used if(!visited[row]) { // Check safety if(isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.add(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.remove(board.size()-1); visited[row] = false; } } } } // Function to solve N-Queen static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); ArrayList<Integer> board = new ArrayList<>(); boolean[] visited = new boolean[n +1]; nQueenUtil(1 n board res visited); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for(ArrayList<Integer> row : res) { System.out.print('['); for(int i = 0; i < row.size(); i++) { System.out.print(row.get(i)); if(i != row.size()-1) System.out.print(' '); } System.out.println(']'); } } }
#Python program to find all solution of N queen problem #using recursion # Function to check if placement is safe def isSafe(board currRow currCol): for i in range(len(board)): placedRow = board[i] placedCol = i + 1 # Check diagonals if abs(placedRow - currRow) == abs(placedCol - currCol): return False # Not safe return True # Safe to place # Recursive utility to solve N-Queens def nQueenUtil(col n board res visited): # If all queens placed add to res if col > n: res.append(board.copy()) return # Try each row in column for row in range(1 n+1): # If row not used if not visited[row]: # Check safety if isSafe(board row col): # Mark row visited[row] = True # Place queen board.append(row) # Recur for next column nQueenUtil(col+1 n board res visited) # Backtrack board.pop() visited[row] = False # Main N-Queen solver def nQueen(n): res = [] board = [] visited = [False] * (n + 1) nQueenUtil(1 n board res visited) return res if __name__ == '__main__': n = 4 res = nQueen(n) for row in res: print(row)
//C# program to find all solution of N queen problem //using recursion using System; using System.Collections.Generic; class GfG { // Check if placement is safe static bool isSafe(List<int> board int currRow int currCol){ for (int i = 0; i < board.Count; i++) { int placedRow = board[i]; int placedCol = i + 1; // Check diagonals if (Math.Abs(placedRow - currRow) == Math.Abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve static void nQueenUtil(int col int n List<int> board List<List<int> > res bool[] visited){ // If all queens placed add to res if (col > n) { res.Add(new List<int>(board)); return; } // Try each row in column for (int row = 1; row <= n; row++) { // If row not used if (!visited[row]) { // Check safety if (isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.Add(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.RemoveAt(board.Count - 1); visited[row] = false; } } } } // Main N-Queen solver static List<List<int>> nQueen(int n){ List<List<int> > res = new List<List<int> >(); List<int> board = new List<int>(); bool[] visited = new bool[n + 1]; nQueenUtil(1 n board res visited); return res; } static void Main(string[] args) { int n = 4; List<List<int>> res = nQueen(n); foreach (var temp in res) { Console.WriteLine('[' + String.Join(' ' temp) + ']'); } } }
//JavaScript program to find all solution of N queen problem //using recursion // Function to check if placement is safe function isSafe(board currRow currCol){ for (let i = 0; i < board.length; i++) { let placedRow = board[i]; let placedCol = i + 1; // Check diagonals if (Math.abs(placedRow - currRow) === Math.abs(placedCol - currCol)) { return false; // Not safe } } return true; // Safe to place } // Recursive utility to solve N-Queens function nQueenUtil(col n board res visited){ // If all queens placed add to res if (col > n) { res.push([...board ]); return; } // Try each row in column for (let row = 1; row <= n; row++) { // If row not used if (!visited[row]) { // Check safety if (isSafe(board row col)) { // Mark row visited[row] = true; // Place queen board.push(row); // Recur for next column nQueenUtil(col + 1 n board res visited); // Backtrack board.pop(); visited[row] = false; } } } } // Main N-Queen solver function nQueen(n){ let res = []; let board = []; let visited = Array(n + 1).fill(false); nQueenUtil(1 n board res visited); return res; } // Driver code let n = 4; let res = nQueen(n); res.forEach(row => console.log(row));
Wyjście
[2 4 1 3] [3 1 4 2]
Złożoność czasowa: O(n!*n) n! do generowania wszystkiego permutacje i O(n) do walidacji każdej permutacji.
Przestrzeń pomocnicza: NA)
[Oczekiwane podejście] — Korzystanie z cofania z przycinaniem — O(n!) czasu i O(n) przestrzeni
Aby zoptymalizować powyższe podejście, możemy zastosować cofanie się z przycinaniem . Zamiast generować wszystkie możliwe permutacje, budujemy rozwiązanie stopniowo, robiąc to, możemy mieć pewność na każdym kroku, że rozwiązanie częściowe pozostaje ważne. Jeśli wystąpi konflikt, natychmiast się wycofamy, to pomaga unikanie niepotrzebny obliczenia .
Realizacja krok po kroku :
- Zacznij od pierwszej kolumny i spróbuj umieścić królową w każdym rzędzie.
- Zachowaj tablice, aby śledzić które wydziwianie są już zajęte. Podobnie w przypadku śledzenia główny I drobne przekątne są już zajęte.
- Jeśli królowa umieszczenie konflikty z istniejącymi królowymi pominąć To wiersz I wracać królową, aby spróbować następnego możliwy rząd (Przycinaj i cofaj się podczas konfliktu).
// C++ program to find all solution of N queen problem by // using backtracking and pruning #include
// Java program to find all solutions of the N-Queens problem // using backtracking and pruning import java.util.ArrayList; import java.util.List; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil(int j int n ArrayList<Integer> board boolean[] rows boolean[] diag1 boolean[] diag2 ArrayList<ArrayList<Integer>> res) { if (j > n) { // A solution is found res.add(new ArrayList<>(board)); return; } for (int i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.add(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.remove(board.size() - 1); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); ArrayList<Integer> board = new ArrayList<>(); // Rows occupied boolean[] rows = new boolean[n + 1]; // Major diagonals (row + j) and Minor diagonals (row - col + n) boolean[] diag1 = new boolean[2 * n + 1]; boolean[] diag2 = new boolean[2 * n + 1]; // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for (ArrayList<Integer> solution : res) { System.out.print('['); for (int i = 0; i < solution.size(); i++) { System.out.print(solution.get(i)); if (i != solution.size() - 1) { System.out.print(' '); } } System.out.println(']'); } } }
# Python program to find all solutions of the N-Queens problem # using backtracking and pruning def nQueenUtil(j n board rows diag1 diag2 res): if j > n: # A solution is found res.append(board[:]) return for i in range(1 n + 1): if not rows[i] and not diag1[i + j] and not diag2[i - j + n]: # Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = True board.append(i) # Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res) # Remove queen (backtrack) board.pop() rows[i] = diag1[i + j] = diag2[i - j + n] = False def nQueen(n): res = [] board = [] # Rows occupied rows = [False] * (n + 1) # Major diagonals (row + j) and Minor diagonals (row - col + n) diag1 = [False] * (2 * n + 1) diag2 = [False] * (2 * n + 1) # Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res) return res if __name__ == '__main__': n = 4 res = nQueen(n) for temp in res: print(temp)
// C# program to find all solutions of the N-Queens problem // using backtracking and pruning using System; using System.Collections.Generic; class GfG { // Utility function for solving the N-Queens // problem using backtracking. static void nQueenUtil(int j int n List<int> board bool[] rows bool[] diag1 bool[] diag2 List<List<int>> res) { if (j > n) { // A solution is found res.Add(new List<int>(board)); return; } for (int i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.Add(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.RemoveAt(board.Count - 1); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. static List<List<int>> nQueen(int n) { List<List<int>> res = new List<List<int>>(); List<int> board = new List<int>(); // Rows occupied bool[] rows = new bool[n + 1]; // Major diagonals (row + j) and Minor diagonals (row - col + n) bool[] diag1 = new bool[2 * n + 1]; bool[] diag2 = new bool[2 * n + 1]; // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } static void Main(string[] args) { int n = 4; List<List<int>> res = nQueen(n); foreach (var temp in res) { Console.WriteLine('[' + String.Join(' ' temp) + ']'); } } }
// JavaScript program to find all solutions of the N-Queens problem // using backtracking and pruning // Utility function for solving the N-Queens // problem using backtracking. function nQueenUtil(j n board rows diag1 diag2 res) { if (j > n) { // A solution is found res.push([...board]); return; } for (let i = 1; i <= n; ++i) { if (!rows[i] && !diag1[i + j] && !diag2[i - j + n]) { // Place queen rows[i] = diag1[i + j] = diag2[i - j + n] = true; board.push(i); // Recurse to the next column nQueenUtil(j + 1 n board rows diag1 diag2 res); // Remove queen (backtrack) board.pop(); rows[i] = diag1[i + j] = diag2[i - j + n] = false; } } } // Solves the N-Queens problem and returns // all valid configurations. function nQueen(n) { const res = []; const board = []; // Rows occupied const rows = Array(n + 1).fill(false); // Major diagonals (row + j) and Minor diagonals (row - col + n) const diag1 = Array(2 * n + 1).fill(false); const diag2 = Array(2 * n + 1).fill(false); // Start solving from the first column nQueenUtil(1 n board rows diag1 diag2 res); return res; } // Driver Code const n = 4; const res = nQueen(n); res.forEach(temp => console.log(temp));
Wyjście
[2 4 1 3] [3 1 4 2]
Złożoność czasowa: O(n!) Do generowania wszystkiego permutacje .
Przestrzeń pomocnicza: NA)
[Podejście alternatywne] – Wycofywanie się przy użyciu maskowania bitów
Aby jeszcze bardziej zoptymalizować cofanie się podejście szczególnie w przypadku większych wartości N możemy użyć maskowanie bitów skutecznie śledzić zajęty rzędy i przekątne. Maskowanie bitów pozwala nam używać liczb całkowitych ( rzędy ld rd ), aby śledzić, które rzędy i przekątne są zajęte, korzystając z funkcji fast operacje bitowe na szybciej obliczenia. Podejście pozostaje takie samo jak powyżej.
Poniżej podano realizacja:
C++//C++ program to find all solution of N queen problem //using recursion #include
// Java program to find all solution of N queen problem // using recursion import java.util.*; class GfG { // Function to check if the current placement is safe static boolean isSafe(int row int col int rows int ld int rd int n) { return !(((rows >> row) & 1) == 1) && !(((ld >> (row + col)) & 1) == 1) && !(((rd >> (row - col + n)) & 1) == 1); } // Recursive function to generate all possible permutations static void nQueenUtil(int col int n ArrayList<Integer> board ArrayList<ArrayList<Integer>> res int rows int ld int rd) { // If all queens are placed add into res if (col > n) { res.add(new ArrayList<>(board)); return; } // Try placing a queen in each row // of the current column for (int row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.add(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.remove(board.size() - 1); } } } // Main function to find all distinct // res to the n-queens puzzle static ArrayList<ArrayList<Integer>> nQueen(int n) { ArrayList<ArrayList<Integer>> res = new ArrayList<>(); // Current board configuration ArrayList<Integer> board = new ArrayList<>(); // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } public static void main(String[] args) { int n = 4; ArrayList<ArrayList<Integer>> res = nQueen(n); for (ArrayList<Integer> solution : res) { System.out.print('['); for (int j = 0; j < n; ++j) { System.out.print(solution.get(j)); if (j != n - 1) System.out.print(' '); } System.out.println(']'); } } }
# Python program to find all solution of N queen problem # using recursion # Function to check if the current placement is safe def isSafe(row col rows ld rd n): return not ((rows >> row) & 1) and not ((ld >> (row + col)) & 1) and not ((rd >> (row - col + n)) & 1) # Recursive function to generate all possible permutations def nQueenUtil(col n board res rows ld rd): # If all queens are placed add into res if col > n: res.append(board[:]) return # Try placing a queen in each row # of the current column for row in range(1 n + 1): # Check if it's safe to place the queen if isSafe(row col rows ld rd n): # Place the queen board.append(row) # Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))) # Backtrack: remove the queen board.pop() # Main function to find all distinct # res to the n-queens puzzle def nQueen(n): res = [] # Current board configuration board = [] # Start solving from the first column nQueenUtil(1 n board res 0 0 0) return res if __name__ == '__main__': n = 4 res = nQueen(n) for solution in res: print('[' end='') for j in range(n): print(solution[j] end='') if j != n - 1: print(' ' end='') print(']')
// C# program to find all solution of N queen problem // using recursion using System; using System.Collections.Generic; class GfG { // Function to check if the current placement is safe static bool isSafe(int row int col int rows int ld int rd int n) { return !(((rows >> row) & 1) == 1) && !(((ld >> (row + col)) & 1) == 1) && !(((rd >> (row - col + n)) & 1) == 1); } // Recursive function to generate all possible permutations static void nQueenUtil(int col int n List<int> board List<List<int>> res int rows int ld int rd) { // If all queens are placed add into res if (col > n) { res.Add(new List<int>(board)); return; } // Try placing a queen in each row // of the current column for (int row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.Add(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.RemoveAt(board.Count - 1); } } } // Main function to find all distinct // res to the n-queens puzzle static List<List<int>> nQueen(int n) { List<List<int>> res = new List<List<int>>(); // Current board configuration List<int> board = new List<int>(); // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } static void Main() { int n = 4; List<List<int>> res = nQueen(n); foreach (var solution in res) { Console.Write('['); for (int j = 0; j < n; ++j) { Console.Write(solution[j]); if (j != n - 1) Console.Write(' '); } Console.WriteLine(']'); } } }
// JavaScript program to find all solution of N queen problem // using recursion // Function to check if the current placement is safe function isSafe(row col rows ld rd n) { return !((rows >> row) & 1) && !((ld >> (row + col)) & 1) && !((rd >> (row - col + n)) & 1); } // Recursive function to generate all possible permutations function nQueenUtil(col n board res rows ld rd) { // If all queens are placed add into res if (col > n) { res.push([...board]); return; } // Try placing a queen in each row // of the current column for (let row = 1; row <= n; ++row) { // Check if it's safe to place the queen if (isSafe(row col rows ld rd n)) { // Place the queen board.push(row); // Recur to place the next queen nQueenUtil(col + 1 n board res rows | (1 << row) (ld | (1 << (row + col))) (rd | (1 << (row - col + n)))); // Backtrack: remove the queen board.pop(); } } } // Main function to find all distinct // res to the n-queens puzzle function nQueen(n) { let res = []; // Current board configuration let board = []; // Start solving from the first column nQueenUtil(1 n board res 0 0 0); return res; } // Driver Code let n = 4; let res = nQueen(n); for (let i = 0; i < res.length; i++) { process.stdout.write('['); for (let j = 0; j < n; ++j) { process.stdout.write(res[i][j].toString()); if (j !== n - 1) process.stdout.write(' '); } console.log(']'); }
Wyjście
[2 4 1 3] [3 1 4 2]
Złożoność czasowa: O(n!) do generowania wszystkich permutacji.
Złożoność przestrzeni: NA)
