- Automaty ze stosem to sposób na wdrożenie CFG w taki sam sposób, w jaki projektujemy DFA dla zwykłej gramatyki. DFA może zapamiętać skończoną ilość informacji, ale PDA może zapamiętać nieskończoną ilość informacji.
- Automaty ze stosem to po prostu NFA wzmocnione „zewnętrzną pamięcią stosu”. Dodanie stosu służy do zapewnienia automatom pushdown możliwości zarządzania pamięcią „ostatni na wejściu, pierwszy na wyjściu”. Automaty ze stosem mogą przechowywać nieograniczoną ilość informacji na stosie. Może uzyskać dostęp do ograniczonej ilości informacji na stosie. PDA może wepchnąć element na górę stosu i zdjąć element ze szczytu stosu. Aby wczytać element na stos, górne elementy muszą zostać oderwane i przepadają.
- PDA jest potężniejsze niż FA. Każdy język, który może zostać zaakceptowany przez FA, może być również zaakceptowany przez PDA. PDA akceptuje również klasę języka, która nawet nie może zostać zaakceptowana przez FA. Zatem PDA jest znacznie lepszy od FA.
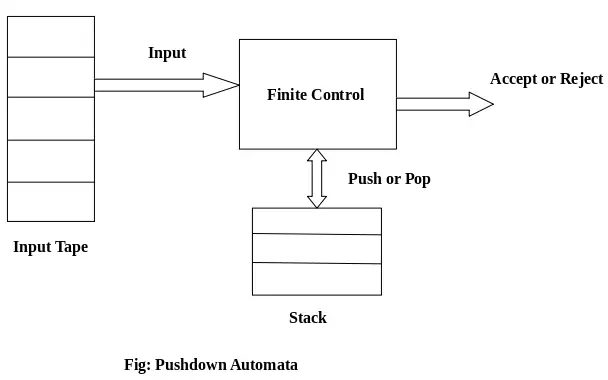
Komponenty PDA:
Taśma wejściowa: Taśma wejściowa jest podzielona na wiele komórek lub symboli. Głowica wejściowa jest tylko do odczytu i może poruszać się tylko od lewej do prawej, po jednym symbolu na raz.
Kontrola skończona: Sterowanie skończone posiada wskaźnik, który wskazuje bieżący symbol, który ma zostać odczytany.
Stos: Stos to struktura, w której możemy wypychać i usuwać elementy tylko z jednego końca. Ma nieskończony rozmiar. W PDA stos służy do tymczasowego przechowywania elementów.
Formalna definicja PDA:
PDA można zdefiniować jako zbiór 7 komponentów:
Q: skończony zbiór stanów
∑: zestaw wejściowy
C: symbol stosu, który można wypychać i zdejmować ze stosu
q0: stan początkowy
mrówka kontra maven
Z: symbol startu znajdujący się w Γ.
F: zbiór stanów końcowych
D: funkcja mapowania, która służy do przejścia od bieżącego stanu do następnego stanu.
Opis natychmiastowy (ID)
Identyfikator to nieformalny zapis sposobu, w jaki PDA oblicza ciąg wejściowy i podejmuje decyzję, czy ciąg ten zostanie zaakceptowany, czy odrzucony.
Opis chwilowy to potrójny (q, w, α) gdzie:
Q opisuje stan obecny.
w opisuje pozostałe dane wejściowe.
indeks górny w ilustratorze
A opisuje zawartość stosu, u góry po lewej stronie.
Notacja kołowrotu:
Znak ⊢ opisuje oznaczenie kołowrotu i oznacza jeden ruch.
Znak ⊢* opisuje sekwencję ruchów.
Na przykład,
(p, b, T) ⊢ (q, w, α)
W powyższym przykładzie, podczas przejścia ze stanu p do q, symbol wejściowy „b” jest zużywany, a wierzch stosu „T” jest reprezentowany przez nowy ciąg α.
Przykład 1:
Zaprojektuj PDA akceptujący język aNB2n.
Rozwiązanie: W tym języku po n liczbach a powinno nastąpić 2n liczby b. Dlatego zastosujemy bardzo prostą logikę i jeśli przeczytamy pojedyncze „a”, umieścimy dwa „a” na stosie. Gdy tylko przeczytamy „b”, wówczas dla każdego pojedynczego „b” ze stosu powinno zostać usunięte tylko jedno „a”.
alternatywa dla xamppa
Identyfikator można skonstruować w następujący sposób:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Teraz, gdy czytamy b, zmienimy stan z q0 na q1 i zaczniemy wyświetlać odpowiednie „a”. Stąd,
δ(q0, b, a) = (q1, ε)
Zatem proces wyskakiwania „b” będzie powtarzany, chyba że wszystkie symbole zostaną odczytane. Należy pamiętać, że działanie trzaskające występuje tylko w stanie q1.
δ(q1, b, a) = (q1, ε)
Po przeczytaniu wszystkich liter b, wszystkie odpowiadające im litery a powinny zostać wyskoczone. Dlatego też, gdy odczytujemy ε jako symbol wejściowy, wówczas na stosie nie powinno być nic. Zatem ruch będzie następujący:
δ(q1, ε, Z) = (q2, ε)
Gdzie
Algebra relacyjna w rdbms
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Możemy podsumować identyfikator jako:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Teraz przeprowadzimy symulację tego PDA dla ciągu wejściowego „aaabbbbbb”.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
Przykład 2:
Zaprojektuj PDA akceptujący język 0N1M0N.
Rozwiązanie: W tym PDA po n zerach następuje dowolna liczba jedynek, po których następuje n zer. Stąd logika projektowania takiego PDA będzie następująca:
Wciśnij wszystkie 0 na stos po napotkaniu pierwszych 0. Następnie, jeśli przeczytamy 1, po prostu nie rób nic. Następnie odczytaj 0 i po każdym odczycie 0 usuń jedno 0 ze stosu.
Na przykład:

Scenariusz ten można zapisać w formie identyfikatora jako:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Teraz przeprowadzimy symulację tego PDA dla ciągu wejściowego „0011100”.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
