Algebra relacyjna jest proceduralnym językiem zapytań. Przedstawia krok po kroku proces uzyskiwania wyniku zapytania. Do wykonywania zapytań używa operatorów.
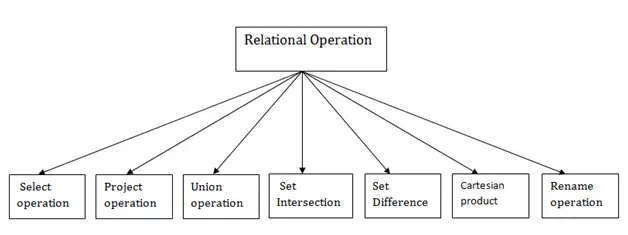
Rodzaje operacji relacyjnych
1. Wybierz operację:
- Operacja Select wybiera krotki spełniające dany predykat.
- Jest to oznaczone sigma (σ).
Notation: σ p(r)
Gdzie:
P służy do przewidywania wyboru
R służy do relacji
P jest używany jako formuła logiki zdań, która może wykorzystywać łączniki takie jak: AND OR i NOT. Te relacyjne mogą być używane jako operatory relacyjne, takie jak =, ≠, ≧, , ≦.
Na przykład: Relacja POŻYCZKA
| NAZWA FILII | KREDYT_NIE | KWOTA |
|---|---|---|
| Śródmieście | L-17 | 1000 |
| Sekwoja | L-23 | 2000 |
| Perryride | L-15 | 1500 |
| Śródmieście | L-14 | 1500 |
| Mianus | L-13 | 500 |
| Roundhill | L-11 | 900 |
| Perryride | L-16 | 1300 |
Wejście:
σ BRANCH_NAME='perryride' (LOAN)
Wyjście:
sztuczna sieć neuronowa
| NAZWA FILII | KREDYT_NIE | KWOTA |
|---|---|---|
| Perryride | L-15 | 1500 |
| Perryride | L-16 | 1300 |
2. Działanie projektu:
- Ta operacja pokazuje listę tych atrybutów, które chcemy, aby pojawiły się w wyniku. Pozostałe atrybuty zostały usunięte z tabeli.
- Jest on oznaczony przez ∏.
Notation: ∏ A1, A2, An (r)
Gdzie
A1 , A2 , A3 jest używany jako nazwa atrybutu relacji R .
Przykład: RELACJE Z KLIENTEM
| NAZWA | ULICA | MIASTO |
|---|---|---|
| Jonesa | Główny | Harrisona |
| Kowal | Północ | Żyto |
| Siano | Główny | Harrisona |
| Curry | Północ | Żyto |
| Johnsona | Dusza | Brooklynie |
| Brooksa | Senator | Brooklynie |
Wejście:
∏ NAME, CITY (CUSTOMER)
Wyjście:
| NAZWA | MIASTO |
|---|---|
| Jonesa | Harrisona |
| Kowal | Żyto |
| Siano | Harrisona |
| Curry | Żyto |
| Johnsona | Brooklynie |
| Brooksa | Brooklynie |
3. Działanie Unii:
- Załóżmy, że istnieją dwie krotki R i S. Operacja sumowania zawiera wszystkie krotki znajdujące się w R, S lub obu w R i S.
- Eliminuje zduplikowane krotki. Jest oznaczony przez ∪.
Notation: R ∪ S
Operacja sumowania musi spełniać następujący warunek:
lista Javy
- R i S muszą mieć atrybut o tej samej liczbie.
- Zduplikowane krotki są eliminowane automatycznie.
Przykład:
RELACJA Z DEPOZYTOREM
| NAZWA KLIENTA | NR KONTA |
|---|---|
| Johnsona | A-101 |
| Kowal | A-121 |
| Mayes | A-321 |
| Tokarz | A-176 |
| Johnsona | A-273 |
| Jonesa | A-472 |
| Lindsay | A-284 |
POŻYCZ RELACJA
| NAZWA KLIENTA | KREDYT_NIE |
|---|---|
| Jonesa | L-17 |
| Kowal | L-23 |
| Hayesa | L-15 |
| Jacksona | L-14 |
| Curry | L-93 |
| Kowal | L-11 |
| Williamsa | L-17 |
Wejście:
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Wyjście:
| NAZWA KLIENTA |
|---|
| Johnsona |
| Kowal |
| Hayesa |
| Tokarz |
| Jonesa |
| Lindsay |
| Jacksona |
| Curry |
| Williamsa |
| Mayes |
4. Ustaw przecięcie:
- Załóżmy, że istnieją dwie krotki R i S. Operacja przecięcia zestawu zawiera wszystkie krotki, które znajdują się w obu R i S.
- Jest to oznaczone przecięciem ∩.
Notation: R ∩ S
Przykład: Korzystając z powyższej tabeli DEPOSITOR i tabeli BORROW
Wejście:
Struktury danych w Javie
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Wyjście:
| NAZWA KLIENTA |
|---|
| Kowal |
| Jonesa |
5. Ustaw różnicę:
- Załóżmy, że istnieją dwie krotki R i S. Operacja przecięcia zestawu zawiera wszystkie krotki znajdujące się w R, ale nie w S.
- Jest to oznaczone przecięciem minus (-).
Notation: R - S
Przykład: Korzystając z powyższej tabeli DEPOSITOR i tabeli BORROW
Wejście:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Wyjście:
| NAZWA KLIENTA |
|---|
| Jacksona |
| Hayesa |
| Williamsa |
| Curry |
6. Iloczyn kartezjański
- Iloczyn kartezjański służy do łączenia każdego wiersza w jednej tabeli z każdym wierszem w drugiej tabeli. Nazywa się go również produktem krzyżowym.
- Jest on oznaczony przez X.
Notation: E X D
Przykład:
PRACOWNIK
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Kowal | A |
| 2 | Złupić | C |
| 3 | Jan | B |
DZIAŁ
| DEPT_NO | DEPT_NAME |
|---|---|
| A | Marketing |
| B | Obroty |
| C | Prawny |
Wejście:
q1 q2 q3 q4
EMPLOYEE X DEPARTMENT
Wyjście:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Kowal | A | A | Marketing |
| 1 | Kowal | A | B | Obroty |
| 1 | Kowal | A | C | Prawny |
| 2 | Złupić | C | A | Marketing |
| 2 | Złupić | C | B | Obroty |
| 2 | Złupić | C | C | Prawny |
| 3 | Jan | B | A | Marketing |
| 3 | Jan | B | B | Obroty |
| 3 | Jan | B | C | Prawny |
7. Zmień nazwę operacji:
Operacja zmiany nazwy służy do zmiany nazwy relacji wyjściowej. Jest oznaczony przez rho (P).
Przykład: Możemy użyć operatora zmiany nazwy, aby zmienić nazwę relacji STUDENT na STUDENT1.
ρ(STUDENT1, STUDENT)
