Wykres kwantyl-kwantyl (wykres q-q) to graficzna metoda określania, czy zbiór danych ma określony rozkład prawdopodobieństwa lub czy dwie próbki danych pochodzą z tego samego populacja albo nie. Wykresy Q-Q są szczególnie przydatne do oceny, czy zbiór danych jest spójny normalnie dystrybuowane lub jeśli wynika z innej znanej dystrybucji. Są powszechnie stosowane w statystyce, analizie danych i kontroli jakości do sprawdzania założeń i identyfikowania odstępstw od oczekiwanych rozkładów.
Kwantyle i percentyle
Kwantyle to punkty w zbiorze danych, które dzielą dane na przedziały zawierające równe prawdopodobieństwa lub proporcje całkowitego rozkładu. Często używa się ich do opisania rozmieszczenia lub dystrybucji zbioru danych. Najpopularniejsze kwantyle to:
- Mediana (50. percentyl) : Mediana to środkowa wartość zbioru danych w kolejności od najmniejszej do największej. Dzieli zbiór danych na dwie równe połowy.
- Kwartyle (25., 50. i 75. percentyl) : Kwartyle dzielą zbiór danych na cztery równe części. Pierwszy kwartyl (Q1) to wartość, poniżej której znajduje się 25% danych, drugi kwartyl (Q2) to mediana, zaś trzeci kwartyl (Q3) to wartość, poniżej której znajduje się 75% danych.
- Percentyle : Percentyle są podobne do kwartylów, ale dzielą zbiór danych na 100 równych części. Na przykład 90. percentyl to wartość, poniżej której przypada 90% danych.
Notatka:
- Wykres q-q to wykres kwantyli pierwszego zbioru danych względem kwantyli drugiego zbioru danych.
- Dla celów informacyjnych wykreślono także linię 45%; Dla jeśli próbki pochodzą z tej samej populacji, wówczas punkty leżą wzdłuż tej linii.
Normalna dystrybucja:
Rozkład normalny (inaczej krzywa Bella rozkładu Gaussa) to ciągły rozkład prawdopodobieństwa reprezentujący rozkład uzyskany z losowo wygenerowanych wartości rzeczywistych.
. 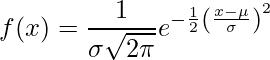

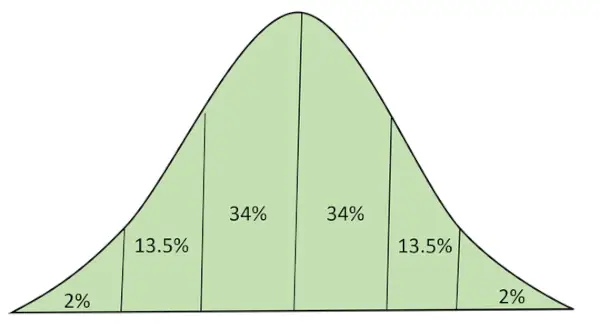
Rozkład normalny z obszarem pod krzywą
Jak narysować wykres Q-Q?
Aby narysować wykres kwantyl-kwantyl (Q-Q), możesz wykonać następujące kroki:
- Zbierz dane : Zbierz zbiór danych, dla którego chcesz utworzyć wykres Q-Q. Upewnij się, że dane są liczbowe i reprezentują losową próbkę z populacji będącej przedmiotem zainteresowania.
- Sortuj dane : Uporządkuj dane w kolejności rosnącej lub malejącej. Ten krok jest niezbędny do dokładnego obliczenia kwantyli.
- Wybierz rozkład teoretyczny : określ rozkład teoretyczny, z którym chcesz porównać swój zbiór danych. Typowe wybory obejmują rozkład normalny, rozkład wykładniczy lub dowolny inny rozkład, który dobrze pasuje do danych.
- Oblicz kwantyle teoretyczne : Oblicz kwantyle dla wybranego rozkładu teoretycznego. Na przykład, jeśli porównujesz rozkład normalny, możesz użyć funkcji odwrotnego rozkładu skumulowanego (CDF) rozkładu normalnego, aby znaleźć oczekiwane kwantyle.
- Konspiratorstwo :
- Narysuj posortowane wartości zbioru danych na osi x.
- Narysuj odpowiednie kwantyle teoretyczne na osi y.
- Każdy punkt danych (x, y) reprezentuje parę wartości obserwowanych i oczekiwanych.
- Połącz punkty danych, aby wizualnie sprawdzić związek między zbiorem danych a rozkładem teoretycznym.
Interpretacja wykresu Q-Q
- Jeśli punkty na wykresie układają się w przybliżeniu wzdłuż linii prostej, sugeruje to, że zbiór danych ma założony rozkład.
- Odchylenia od linii prostej wskazują na odstępstwa od założonego rozkładu, wymagające dalszych badań.
Badanie podobieństwa rozkładu za pomocą wykresów Q-Q
Badanie podobieństwa rozkładów za pomocą wykresów Q-Q jest podstawowym zadaniem statystyki. Porównanie dwóch zbiorów danych w celu ustalenia, czy pochodzą z tej samej dystrybucji, jest niezbędne do różnych celów analitycznych. Jeśli założenie o wspólnym rozkładzie zostanie spełnione, połączenie zbiorów danych może poprawić dokładność estymacji parametrów, takich jak lokalizacja i skala. Wykresy Q-Q, skrót od wykresów kwantylowo-kwantylowych, oferują wizualną metodę oceny podobieństwa rozkładów. Na tych wykresach kwantyle z jednego zbioru danych są wykreślane z kwantylami z innego. Jeśli punkty ściśle pokrywają się wzdłuż linii ukośnej, sugeruje to podobieństwo rozkładów. Odchylenia od tej przekątnej wskazują na różnice w charakterystyce rozkładu.
Podczas gdy testy takie jak chi-kwadrat I Kołmogorow-Smirnow testy mogą ocenić ogólne różnice w rozkładzie, wykresy Q-Q zapewniają szczegółową perspektywę poprzez bezpośrednie porównanie kwantyli. Umożliwia to analitykom dostrzeżenie konkretnych różnic, takich jak zmiany lokalizacji lub zmiany skali, które mogą nie być oczywiste na podstawie samych formalnych testów statystycznych.
Implementacja wykresu Q-Q w języku Python
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Wyjście:
Fabuła Q-Q
Tutaj, ponieważ punkty danych w przybliżeniu układają się po linii prostej na wykresie Q-Q, sugeruje to, że zbiór danych jest zgodny z założonym rozkładem teoretycznym, który w tym przypadku przyjęliśmy za rozkład normalny.
Zalety działki Q-Q
- Elastyczne porównanie : Wykresy Q-Q umożliwiają porównywanie zbiorów danych o różnych rozmiarach bez wymagające jednakowej wielkości próbek.
- Analiza bezwymiarowa : Są bezwymiarowe, dzięki czemu nadają się do porównywania zbiorów danych różne jednostki lub skale.
- Interpretacja wizualna : Zapewnia wyraźną wizualną reprezentację rozkładu danych w porównaniu z rozkładem teoretycznym.
- Wrażliwy na odchylenia : Z łatwością wykrywa odchylenia od założonych rozkładów, pomagając w identyfikacji rozbieżności w danych.
- Narzędzie diagnostyczne : Pomaga w ocenie założeń dotyczących dystrybucji, identyfikowaniu wartości odstających i zrozumieniu wzorców danych.
Zastosowania wykresu kwantylowo-kwantylowego
Wykres kwantyl-kwantyl służy do następujących celów:
- Ocena założeń dystrybucyjnych : Wykresy Q-Q są często używane do wizualnego sprawdzania, czy zbiór danych ma określony rozkład prawdopodobieństwa, taki jak rozkład normalny. Porównując kwantyle obserwowanych danych z kwantylami założonego rozkładu, można wykryć odchylenia od założonego rozkładu. Ma to kluczowe znaczenie w wielu analizach statystycznych, gdzie ważność założeń dystrybucyjnych wpływa na dokładność wniosków statystycznych.
- Wykrywanie wartości odstających : Wartości odstające to punkty danych, które znacznie odbiegają od reszty zbioru danych. Wykresy Q-Q mogą pomóc w identyfikacji wartości odstających, ujawniając punkty danych, które odbiegają daleko od oczekiwanego wzorca rozkładu. Wartości odstające mogą pojawiać się jako punkty odbiegające od oczekiwanej linii prostej na wykresie.
- Porównywanie dystrybucji : Wykresy Q-Q można wykorzystać do porównania dwóch zbiorów danych w celu sprawdzenia, czy pochodzą one z tego samego rozkładu. Osiąga się to poprzez wykreślenie kwantyli jednego zbioru danych z kwantylami innego zbioru danych. Jeśli punkty leżą w przybliżeniu wzdłuż linii prostej, sugeruje to, że oba zbiory danych pochodzą z tego samego rozkładu.
- Ocena normalności : Wykresy Q-Q są szczególnie przydatne do oceny normalności zbioru danych. Jeśli punkty danych na wykresie ściśle układają się wzdłuż linii prostej, oznacza to, że zbiór danych ma w przybliżeniu rozkład normalny. Odchylenia od linii sugerują odstępstwa od normalności, co może wymagać dalszych badań lub nieparametrycznych technik statystycznych.
- Walidacja modelu : W takich dziedzinach jak ekonometria i uczenie maszynowe wykresy Q-Q służą do sprawdzania poprawności modeli predykcyjnych. Porównując kwantyle zaobserwowanych odpowiedzi z kwantylami przewidywanymi przez model, można ocenić, jak dobrze model pasuje do danych. Odchylenia od oczekiwanego wzorca mogą wskazywać obszary, w których model wymaga poprawy.
- Kontrola jakości : Wykresy Q-Q wykorzystuje się w procesach kontroli jakości w celu monitorowania rozkładu zmierzonych lub zaobserwowanych wartości w czasie lub w różnych partiach. Odstępstwa od oczekiwanych wzorców na wykresie mogą sygnalizować zmiany w leżących u ich podstaw procesach, skłaniając do dalszych badań.
Rodzaje wykresów Q-Q
Istnieje kilka typów wykresów Q-Q powszechnie stosowanych w statystyce i analizie danych, każdy dostosowany do różnych scenariuszy lub celów:
- Normalna dystrybucja : Rozkład symetryczny, w którym wykres Q-Q przedstawiałby punkty w przybliżeniu wzdłuż linii ukośnej, jeśli dane odpowiadają rozkładowi normalnemu.
- Rozkład prawoskrętny : Rozkład, w którym wykres Q-Q będzie przedstawiał wzór, w którym obserwowane kwantyle odchylają się od linii prostej w kierunku górnego końca, wskazując dłuższy ogon po prawej stronie.
- Rozkład lewoskrętny : Rozkład, w którym wykres Q-Q wykazywałby wzór, w którym obserwowane kwantyle odchylają się od linii prostej w kierunku dolnego końca, wskazując dłuższy ogon po lewej stronie.
- Dystrybucja słabo rozproszona : Rozkład, w którym wykres Q-Q pokazywałby obserwowane kwantyle skupione ciaśniej wokół linii ukośnej w porównaniu z kwantylami teoretycznymi, co sugeruje niższą wariancję.
- Dystrybucja nadmiernie rozproszona : Rozkład, w którym wykres Q-Q przedstawiałby obserwowane kwantyle bardziej rozłożone lub odbiegające od linii ukośnej, wskazując większą wariancję lub rozproszenie w porównaniu z rozkładem teoretycznym.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Wyjście:
Wykres Q-Q dla różnych rozkładów
eksploracja danych
