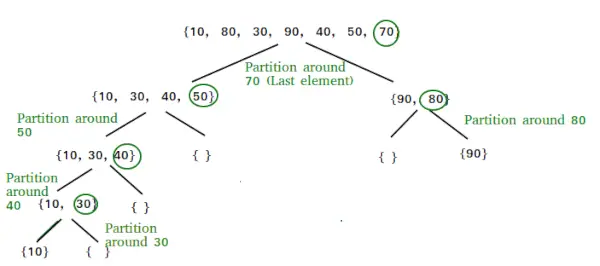
Szybkie sortowanie to wewnętrzny algorytm oparty na strategii dziel i zwyciężaj. W tym:
- Zbiór elementów jest dzielony na części wielokrotnie, aż nie będzie już możliwości dalszego podziału.
- Znany jest również jako sortowanie przez wymianę partycji .
- Wykorzystuje kluczowy element (pivot) do partycjonowania elementów.
- Jedna lewa przegroda zawiera wszystkie elementy mniejsze od osi obrotu, a jedna prawa przegroda zawiera wszystkie elementy większe od elementu kluczowego.
 Sortowanie przez scalanie jest algorytmem zewnętrznym, opartym na strategii dziel i zwyciężaj. W tym:
Sortowanie przez scalanie jest algorytmem zewnętrznym, opartym na strategii dziel i zwyciężaj. W tym:
boto3
- Elementy są dzielone na dwie podtablice (n/2) raz po raz, aż pozostanie tylko jeden element.
- Sortowanie przez scalanie wykorzystuje dodatkową pamięć do sortowania tablicy pomocniczej.
- Sortowanie przez scalanie wykorzystuje trzy tablice, z których dwie służą do przechowywania każdej połowy, a trzecia zewnętrzna służy do przechowywania ostatecznej posortowanej listy poprzez połączenie pozostałych dwóch, a każda tablica jest następnie sortowana rekurencyjnie.
- Na koniec wszystkie podtablice są łączone, aby uzyskać rozmiar n elementów tablicy.

Sortowanie szybkie a sortowanie przez scalanie
- Podział elementów w tablicy: Podczas sortowania przez scalanie tablica jest dzielona tylko na 2 połowy (tj. n/2). podczas gdy w przypadku szybkiego sortowania tablica jest dzielona na dowolny stosunek. Przy sortowaniu szybkim nie ma konieczności dzielenia tablicy elementów na równe części. Złożoność najgorszego przypadku: Najgorsza złożoność szybkiego sortowania to O(n^2), ponieważ istnieje potrzeba wielu porównań w najgorszym stanie. podczas gdy w przypadku sortowania przez scalanie najgorszy przypadek i średni przypadek mają tę samą złożoność O (n log n). Użycie ze zbiorami danych: Sortowanie przez scalanie może dobrze działać w przypadku dowolnego typu zbiorów danych, niezależnie od ich rozmiaru (dużych lub małych). mając na uwadze, że szybkie sortowanie nie działa dobrze w przypadku dużych zbiorów danych. Dodatkowe wymagania dotyczące miejsca w pamięci: sortowanie przez scalanie nie jest dostępne, ponieważ wymaga dodatkowej przestrzeni pamięci do przechowywania tablic pomocniczych. natomiast szybkie sortowanie jest dostępne, ponieważ nie wymaga dodatkowego przechowywania. Wydajność: sortowanie przez scalanie jest bardziej wydajne i działa szybciej niż sortowanie szybkie w przypadku większego rozmiaru tablicy lub zestawów danych. podczas gdy sortowanie szybkie jest bardziej wydajne i działa szybciej niż sortowanie przez scalanie w przypadku mniejszego rozmiaru tablicy lub zestawów danych. Metoda sortowania: Sortowanie szybkie to metoda sortowania wewnętrznego, w której dane są sortowane w pamięci głównej. mając na uwadze, że sortowanie przez scalanie jest zewnętrzną metodą sortowania, w której dane przeznaczone do sortowania nie mieszczą się w pamięci i do sortowania potrzebna jest pamięć pomocnicza. Stabilność: Sortowanie przez scalanie jest stabilne, ponieważ dwa elementy o tej samej wartości pojawiają się w tej samej kolejności na posortowanych wynikach, jak w nieposortowanej tablicy wejściowej. podczas gdy szybkie sortowanie jest niestabilne w tym scenariuszu. Ale można go ustabilizować, wprowadzając pewne zmiany w kodzie. Preferowane dla: W przypadku tablic preferowane jest szybkie sortowanie. natomiast sortowanie przez scalanie jest preferowane w przypadku list połączonych. Miejsce odniesienia: Quicksort wykazuje dobrą lokalizację pamięci podręcznej, co sprawia, że szybkie sortowanie jest szybsze niż sortowanie przez scalanie (w wielu przypadkach, jak w środowisku pamięci wirtualnej).
| Podstawa porównania | Szybkie sortowanie | Sortowanie przez scalanie |
|---|---|---|
| Podział elementów tablicy | Podział szeregu elementów odbywa się w dowolnym stosunku, niekoniecznie podzielonym na połowę. | Podczas sortowania przez scalanie tablica jest dzielona tylko na 2 połowy (tj. n/2). |
| Złożoność najgorszego przypadku | O(n^2) | O(nlogn) |
| Działa dobrze | Działa dobrze na mniejszych tablicach | Działa dobrze na tablicy dowolnego rozmiaru |
| Szybkość wykonania | Działa szybciej niż inne algorytmy sortowania dla małych zbiorów danych, takie jak sortowanie przez wybór itp | Ma stałą prędkość dla dowolnego rozmiaru danych |
| Dodatkowe zapotrzebowanie na miejsce do przechowywania | Mniej (na miejscu) | Więcej (nie na miejscu) |
| Efektywność | Nieefektywne w przypadku większych tablic | Bardziej wydajny |
| Metoda sortowania | Wewnętrzny | Zewnętrzny |
| Stabilność | Niestabilny | Stabilny |
| Preferowane dla | dla tablic | dla list połączonych |
| Miejscowość odniesienia | Dobry | słaby |
| Główna praca | Główną pracą jest podzielenie tablicy na dwie podtablice przed ich rekurencyjnym posortowaniem. | Główną pracą jest połączenie dwóch podtablic po ich rekurencyjnym posortowaniu. |
| Podział tablicy | Podział tablicy na podtablice może, ale nie musi, być zrównoważony, ponieważ tablica jest podzielona wokół osi. | Podział tablicy na podtablice jest zawsze zrównoważony, ponieważ dzieli tablicę dokładnie pośrodku. |
| metoda | Sortowanie szybkie to metoda sortowania na miejscu. | Sortowanie przez scalanie nie jest metodą sortowania miejscowego. |
| Łączenie | Quicksort nie wymaga jawnego łączenia posortowanych podtablic; raczej podtablice zostały odpowiednio uporządkowane podczas partycjonowania. | Sortowanie przez scalanie wykonuje jawne scalanie posortowanych podtablic. |
| Przestrzeń | Quicksort nie wymaga dodatkowej przestrzeni w tablicy. | Do łączenia posortowanych podtablic potrzebna jest tablica tymczasowa o rozmiarze równym liczbie elementów wejściowych. |
