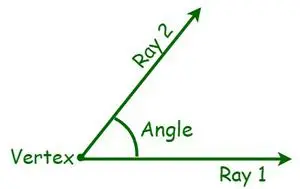
W geometrii kąt jest podstawową miarą kształtu geometrycznego. Kąt definiuje się jako stopień obrotu wokół punktu przecięcia dwóch linii lub płaszczyzn, który jest wymagany do dopasowania jednej do drugiej. Istnieją różne rodzaje kątów, oparte na pomiarze kąta. Mierzy się ją w stopniach lub radianach. Kąt to kształt utworzony przez dwie linie lub półproste, które odchodzą od wspólnego punktu zwanego wierzchołkiem. Kiedy dwa promienie przecinają się, to znaczy, gdy rzutowane są półproste ze wspólnym punktem końcowym, powstaje kąt. Teraz wspólne punkty końcowe nazywane są wierzchołkami, podczas gdy promienie są znane jako ramiona.
Rodzaje kątów

- Kąt ostry: Kąt ostry to kąt większy niż 0 stopni i mniejszy niż 90 stopni, tj. Mieści się w zakresie od 0° do 90° (oba wyłączne).
- Prosty kąt: Kąt prosty nazywany jest kątem, który mierzy dokładnie 90 stopni.
- Kąt rozwarty: Kąt rozwarty to kąt większy niż 90 stopni i mniejszy niż 180 stopni, tj. Mieści się w zakresie od 90° do 180° (oba wyłączne).
- Kąt prosty: Kąt prosty nazywany jest kątem, który ma dokładnie 180 stopni.
- Kąt odbicia: Kąt wklęsły to kąt większy niż 180 stopni i mniejszy niż 360 stopni, tj. Mieszczący się w zakresie od 180° do 360° (oba wyłączne).
- Pełny kąt lub pełny obrót: Kąt pełny nazywany jest kątem, który mierzy dokładnie 360 stopni.
Istnieją również inne typy kątów, takie jak kąty dopełniające, kąty dodatkowe oraz kąty przyległe i nieprzylegające.
- Kąty komplementarne: Mówi się, że dwa kąty są dopełniające, jeśli ich suma jest kątem prostym, tj. 90°.
- Kąty dodatkowe: Mówi się, że dwa kąty są dopełniające, jeśli ich suma wynosi 180°.
- Sąsiednie kąty: Mówi się, że dwa kąty są sąsiadujące, jeśli mają wspólny wierzchołek i wspólne ramię.
- Kąty nieprzylegające: Mówi się, że dwa kąty nie sąsiadują ze sobą, jeśli nie mają wspólnego wierzchołka i wspólnego ramienia.
Wzór na znajdowanie kątów
Istnieją różne rodzaje wzorów na znalezienie kąta; niektóre z nich to wzór na kąt środkowy, wzór na podwójny kąt, wzór na półkąt, wzór na kąt złożony, wzór na kąt wewnętrzny itp.
- Do określenia kąta odcinka utworzonego na okręgu używamy wzoru na kąt środkowy.
- Aby określić brakujący kąt w wielokącie, używamy wzoru na sumę kątów wewnętrznych.
- Aby znaleźć brakujący kąt w trójkącie prostokątnym, używamy stosunków trygonometrycznych.
- Do znalezienia brakującego kąta w trójkącie innym niż prostokątny używamy twierdzenia sinusów lub twierdzenia cosinusów.
Nazwa formuły | Formuła | Jak znaleźć nieznany kąt? |
|---|---|---|
| Wzór na kąt środkowy | θ = (s × 360°)/2prTutaj s to długość łuku, a r to promień okręgu | Zastąp wartości długości łuku i promienia okręgu, aby określić kąt odcinka utworzonego na okręgu. |
| Wzór na sumę kątów wewnętrznych | 180°(n-2)Tutaj n jest liczbą boków wielokąta | Aby wyznaczyć nieznany kąt wewnętrzny wielokąta, najpierw oblicz sumę wszystkich kątów wewnętrznych za pomocą tego wzoru, a następnie odejmij od wyniku sumę wszystkich znanych kątów. |
| Stosunki trygonometryczne | sin θ = przeciwna strona/przeciwprostokątnacos θ = sąsiedni bok/przeciwprostokątnatan θ = strona przeciwna/strona sąsiednia | W zależności od dostępnych dwóch boków trójkąta prostokątnego wybierz jeden z tych stosunków trygonometrycznych, aby znaleźć nieznany kąt. |
| Prawo sinusów | a/sin A = b/sin B = c/sin CTutaj A, B i C są kątami wewnętrznymi trójkąta, a a, b i c są ich przeciwległymi bokami. string.zawiera Java | Kiedy znamy dwa boki i kąt nieuwzględniony (lub) dwa kąty i bok nieuwzględniony, wówczas twierdzenie sinusów można zastosować do określenia nieznanych kątów trójkąta. |
| Prawo cosinusów | A2= b2+ c2– 2bc cos AB2= ok2+ za2– 2ca cos BC2= za2+ b2– 2ab cos CTutaj A, B i C są kątami wewnętrznymi trójkąta, a a, b i c są ich przeciwległymi bokami. | Kiedy znamy trzy boki (lub) dwa boki i kąt zawarty w nich, wówczas twierdzenie cosinusów można zastosować do określenia nieznanych kątów trójkąta. |
Przykładowe pytania
Zadanie 1: Znajdź kąt w wierzchołku B danego trójkąta, korzystając z jednego ze wzorów trygonometrycznych na znalezienie kątów.

Rozwiązanie:
Dany,
BC = 3 jednostki = Sąsiedni bok θ.
AC = 4 jednostki = Przeciwna strona θ.
W tym przypadku znamy zarówno przeciwną, jak i sąsiednią stronę θ. Dlatego możemy użyć wzoru na tangens, aby znaleźć θ.
⇒ tan θ = strona przeciwna/strona sąsiednia
⇒ tan θ = 4/3
⇒ θ = opalenizna-1(4/3) ⇒ θ = 53,1°
rozłożyste drzewaZatem kąt przy wierzchołku B wynosi 53,1°.
Pytanie 2: Znajdź kąty w wierzchołkach X i Y, jeśli ∠Z = 35° i x = 3 cale, y = 8 cali i z = 3,5 cala.

Rozwiązanie:
Dany,
∠Z = 35° i x = 6 cali, y = 3 cale i z = 3,5 cala
Ponieważ znamy wszystkie trzy boki i kąt, możemy skorzystać ze wzoru na sinus.
Ze wzoru na regułę sinusową mamy
x/sin X = y/sin Y = z/sin Z
Teraz,
y/sin Y = z/sin Z
⇒ 3/grzech Y = 3,5/grzech 35°
⇒ 3/bez Y = 3,5/0,574 {Ponieważ grzech 35° = 0,574}
⇒ grzech Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = grzech−1(0,492) = 29,47°
Wiemy, że suma trzech kątów w trójkącie wynosi 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
zmienna globalna JavaScript⇒ ∠X = 180° – 64,47° = 115,53°
Stąd ∠X = 115,53° i ∠Y = 29,47°.
Pytanie 3: Oblicz piąty kąt wewnętrzny pięciokąta, jeśli cztery jego kąty wewnętrzne wynoszą 110°, 85°, 136° i 105°.
Rozwiązanie:
Liczba boków pięciokąta (n) = 5.
Teraz suma wszystkich 5 kątów wewnętrznych pięciokąta = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Suma danych 4 kątów wewnętrznych = 110°+ 85°+ 136°+ i 105°= 436°.
Zatem piąty kąt wewnętrzny = 540° – 436° = 104°
Zatem piąty kąt wewnętrzny pięciokąta wynosi 104°.
Pytanie 4: Wyznacz wartość y oraz miarę kątów na podanej figurze.

Rozwiązanie:
Z podanego rysunku możemy zauważyć, że (4y – 6)° i (3y + 5)° są kątami dopełniającymi, czyli suma (4y – 6)° i (3y + 5)° wynosi 90 °.
⇒ (4 lata – 6)° + (3 lata + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7 lat = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Teraz (4 lata – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Zadanie 5: Znajdź kąt w wierzchołku Q w danym trójkącie, korzystając z jednego ze wzorów na znalezienie kątów.

Rozwiązanie:
Biorąc pod uwagę, p = QR = 6 cm, q = PR = 9 cm i r = PQ = 7 cm.
anonimowa funkcja JavaPonieważ znamy wszystkie trzy boki i kąt, możemy użyć wzoru na regułę cosinusa, aby znaleźć wierzchołek kąta Q.
⇒ q2= str2+ r2– 2 pr za Q
⇒ 92= 62+ 72– 2 (6) (7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84 cos Q
⇒ 84 coc Q = 81 – 85
⇒ 84 coc Q = -4
⇒ sałata Q = -4/84 = -1/21
⇒ ∠Q = sałata-1(-1/21) = 92,72°
Stąd kąt przy wierzchołku Q, ∠Q = 92,72°.
Pytanie 6: Oblicz kąt odcinka utworzonego na okręgu, jeśli długość łuku wynosi 12π, a promień wynosi 9 cm.
Rozwiązanie:
Dany,
Długość łuku = 12π
Promień (r) = 9 cm
Teraz wzór na kąt wygląda następująco:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12×360°/10
⇒ θ = 240°
Zatem kąt wynosi 240°.
