Wzory Sin Cos w trygonometrii: Trygonometria, jak sama nazwa wskazuje, to nauka o trójkątach. Jest to ważna gałąź matematyki, która bada związek między długościami boków i kątami trójkąta prostokątnego, a także pomaga w określaniu brakujących długości boków lub kątów trójkąta. Istnieje sześć stosunków lub funkcji trygonometrycznych: sinus, cosinus, tangens, cosecans, secans i cotangens, gdzie cosecans, secans i cotangens są odwrotnością funkcji pozostałych trzech funkcji, tj. odpowiednio sinusa, cosinusa i tangensa.
Stosunek trygonometryczny definiuje się jako stosunek długości boków trójkąta prostokątnego. Trygonometria jest wykorzystywana w różnych dziedzinach naszego codziennego życia. Pomaga określić wysokość wzgórz lub budynków. Jest również stosowany w takich dziedzinach jak kryminologia, budownictwo, fizyka, archeologia, inżynieria silników morskich itp.
W tym artykule omówimy wszystko wzory trygonometryczne, głównie wzory na grzech i cos z ich przykładami oraz listę wszystkich wzorów w trygonometrii.
Spis treści
- Wzory w trygonometrii
- Niektóre podstawowe wzory na grzech
- Tabela formuł grzechu cos
- Przykłady formuł Sin Cos
- Ćwicz problemy dotyczące wzorów sin cos w trygonometrii z przykładami
Wzory w trygonometrii
Rozważmy trójkąt prostokątny XYZ, gdzie ∠Y = 90°. Niech kąt przy wierzchołku Z będzie θ. Strona sąsiadująca z θ nazywana jest stroną sąsiednią, a strona przeciwna do θ nazywana jest stroną przeciwną. Przeciwprostokątna to bok przeciwny do kąta prostego lub najdłuższy bok kąta prostego.
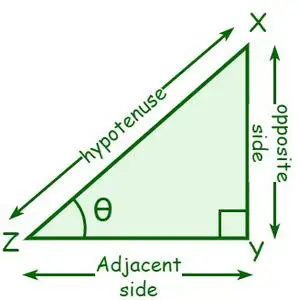
- sin θ = strona przeciwna/przeciwprostokątna
- cos θ = sąsiadujący bok/przeciwprostokątna
- tan θ = strona przeciwna/strona sąsiadująca
- cosec θ = 1/sin θ = przeciwprostokątna/strona przeciwna
- sec θ = 1/ cos θ = Przeciwprostokątna/strona sąsiadująca
- łóżko θ = 1/ tan θ = strona sąsiadująca/strona przeciwna
Wzór sinusa
Sinus kąta w trójkącie prostokątnym to stosunek długości przeciwnego boku do długości przeciwprostokątnej danego kąta. Funkcja sinus jest reprezentowana jako grzech.
sin θ = strona przeciwna/przeciwprostokątna
Wzór cosinusa
Cosinus kąta w trójkącie prostokątnym to stosunek długości sąsiedniego boku do długości przeciwprostokątnej danego kąta. Funkcja cosinus jest reprezentowana jako cos.
skaner.next Javacos θ = sąsiadujący bok/przeciwprostokątna
Niektóre podstawowe wzory na grzech
Funkcje sinus i cosinus w ćwiartkach
- Funkcja sinus jest dodatnia w pierwszej i drugiej ćwiartce oraz ujemna w trzeciej i czwartej ćwiartce.
- Funkcja cosinus jest dodatnia w pierwszej i czwartej ćwiartce oraz ujemna w drugiej i trzeciej ćwiartce.
Stopni
Kwadrant
Znak funkcji sinus
Znak funkcji cosinus
0° do 90°
1. ćwiartka
+ (pozytywny)
+ (pozytywny)
90° do 180°
2. ćwiartka
+ (pozytywny)
- (negatywny)
180° do 270°
Trzecia ćwiartka
- (negatywny)
- (negatywny)
270° do 360°
4. ćwiartka
- (negatywny)
+ (pozytywny)
Tożsamość kąta ujemnego funkcji sinus i cosinus
- Sinus kąta ujemnego jest zawsze równy ujemnemu sinusowi kąta.
grzech (– θ) = – grzech θ
- Cosinus kąta ujemnego jest zawsze równy cosinusowi kąta.
cos (– θ) = cos θ
Zależność funkcji sinus i cosinus
grzech θ = cos (90° – θ)
Funkcje wzajemne funkcji sinus i cosinus
- Funkcja cosecant jest funkcją odwrotną funkcji sinus.
cosec θ = 1/sin θ
- Funkcja sieczna jest funkcją odwrotną funkcji cosinus.
sec θ = 1/cos θ
Tożsamość pitagorejska
bez 2 θ + sałata 2 θ = 1
Okresowe tożsamości funkcji sinus i cosinus
grzech (θ + 2nπ) = grzech θ
cos (θ + 2nπ) = cos θ
Wzory na kąt podwójny dla funkcji sinus i cosinus
grzech 2θ = 2 grzech θ cos θ
cos 2θ = cos 2 θ – grzech 2 θ = 2 sałata 2 θ – 1 = 1 – 2 grzech 2 I
Tożsamości półkątowe dla funkcji sinus i cosinus
grzech (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Tożsamości kąta potrójnego dla funkcji sinus i cosinus
grzech 3θ = 3 grzech θ – 4 grzech 3 I
cos 3θ = 4cos 3 θ – 3 cos θ
Wzory na sumę i różnicę
- Funkcja sinus
grzech (A + B) = grzech A cos B + cos A grzech B
grzech (A – B) = grzech A cos B – cos A grzech B
- Funkcja cosinus
cos (A + B) = cos A cos B – grzech A grzech B
cos (A – B) = cos A cos B + grzech A grzech B
Prawo sinusów lub reguła sinusów
Zasada sinusów to prawo trygonometryczne określające zależność między długościami boków i kątami trójkąta.

a/sin A = b/sin B = c/sin C
Gdzie a, b i c to długości trzech boków trójkąta ABC, a A, B i C to kąty.
Prawo cosinusów
Prawo cosinusów reguły cosinusów służy do określania brakujących lub nieznanych kątów lub długości boków trójkąta.

A 2 = b 2 + c 2 – 2bc cos A
B 2 = ok 2 + za 2 – 2ca cos B
C 2 = za 2 + b 2 – 2ab cos C
Gdzie a, b i c to długości trzech boków trójkąta ABC, a A, B i C to kąty.
Tabela formuł sin cos
Oto tabela/lista wzorów sin i cos dla różnych kątów w stopniach i radianach:
Lista formuł grzechu
| Kąt (w stopniach) | Kąt (w radianach) | grzech I | bo θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | str. 6 | 1/2 | _3/2 |
| 45° | s./4 | 1/√2 | 1/√2 |
| 60° | s./3 | √3/2 | 1/2 |
| 90° | str./2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Liczba Pi | 0 | -1 |
Przykłady formuł Sin Cos
Zadanie 1: Jeśli cos α = 24/25, to znajdź wartość sin α.
Rozwiązanie:
Dany,
cos α = 24/25
Z tożsamości pitagorejskich mamy;
sałata2θ + grzech2θ = 1
(24/25)2+ bez2α = 1
bez2α = 1 – (24/25)2
bez2α = 1 – (576/625) = (625 – 576)/625
bez2α = (625 – 576)/625 = 49/626
grzech α = √49/625 = ±7/25
Zatem sin α = ±7/25.
Zadanie 2: Udowodnić wzory na sin 2A i cos 2A, jeśli ∠A= 30°.
Rozwiązanie:
Biorąc pod uwagę, ∠A= 30°
tablica w JavieWiemy to,
1) grzech 2A = 2 grzech A cos A
grzech 2(30°) = 2 grzech 30° cos 30°
grzech 60° = 2 × (1/2) × (√3/2) {Ponieważ grzech 30° = 1/2, cos 30° = √3/2 i grzech 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Ponieważ cos 60° = 1/2 i cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Stąd udowodnione.
Zadanie 3: Znajdź wartość cos x, jeśli tan x = 3/4.
Rozwiązanie:
Biorąc pod uwagę, tan x = 3/4
Wiemy to,
tan x = strona przeciwna/strona sąsiednia = 3/4
Aby znaleźć przeciwprostokątną, używamy twierdzenia Pitagorasa:
przeciwprostokątna2= naprzeciwko2+ sąsiadujący2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Teraz cos x = sąsiedni bok/przeciwprostokątna
cos x = 4/5
Zatem wartość cos x wynosi 4/5.
Zadanie 4: Znajdź ∠C (w stopniach) i ∠A (w stopniach), jeśli ∠B = 45°, BC = 15 cali i AC = 12 cali.

Rozwiązanie:
Dane: ∠B = 45°, BC = a = 15 cali i AC = b = 12 cali.
Z twierdzenia sinusów mamy
a/sin A = b/sin B = c/sin C
⇒ a/grzech A = b/grzech B
⇒ 15/grzech A = 12/grzech 45°
⇒ 15/grzech A = 12/(1/√2)
⇒ 15/grzech A = 12√2 = 16,97
⇒ bez A = 15/16,97 = 0,8839
⇒ ∠A = grzech-1(0,8839) = 62,11°
Wiemy, że suma kątów wewnętrznych w trójkącie wynosi 180°.
Zatem ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Stąd ∠A = 62,11° i ∠C = 72,89°.
Zadanie 5: Udowodnij tożsamość półkątną funkcji cosinus.
Rozwiązanie:
Tożsamość półkątowa funkcji cosinus wynosi:
cos (θ/2) = ±√[(1 + cos θ)/2]
Z tożsamości podwójnego kąta mamy,
cos 2A = 2 cos2A – 1
Teraz zamień A na θ/2 po obu stronach
⇒ sałata 2(θ/2) = 2 sałata2(i/2) – 1
⇒ sałata θ = 2 sałata2(i/2) – 1
⇒ 2co2(θ/2) = cos θ + 1
⇒ kosm2(θ/2) = (cos θ + 1)/2
⇒ sałata (θ/2) = ±√[(1 + cos θ)/2]
Stąd udowodnione.
Ćwicz problemy dotyczące wzorów sin cos w trygonometrii z przykładami
1. Biorąc pod uwagę sin θ = 3/5. Znajdź cos θ.
2. Udowodnij tożsamość sin(2A) = 2 sinA cosA dla A=45∘.
3. Jeśli cos α = 5/13. Znajdź grzech(2a).
4. Znajdź θ jeśli sin θ = cos(90∘−θ).
5. Jeśli tan β = 2. Znajdź sin β i cos β, korzystając z tożsamości pitagorejskiej.
Często zadawane pytania dotyczące wzorów sin cos w trygonometrii z przykładami
Jakie są podstawowe wzory na sinus i cosinus w trygonometrii?
Podstawowe wzory na sinus i cosinus to sin θ = przeciwprostokątna/przeciwprostokątna i cos θ = sąsiadująca/przeciwprostokątna, gdzie θ jest kątem w trójkącie prostokątnym.
Jak znaleźć sinus i cosinus specjalnych kątów?
Kąty specjalne, takie jak 0∘, 30∘, 45∘, 60∘ i 90∘, mają określone wartości sinusów i cosinusów, które można zapamiętać, korzystając z tabel trygonometrycznych lub koncepcji okręgu jednostkowego.
Jaki jest związek między funkcjami sinus i cosinus?
Funkcje sinus i cosinus są powiązane tożsamością grzech θ = cos(90∘- θ) i tożsamość pitagorejska bez 2 θ+cos 2 θ = 1.
Jak korzystać ze wzorów na kąt podwójny dla sinusa i cosinusa?
Są wzory na kąt podwójny grzech(2θ) = 2sinθcosθ I cos(2θ)=cos 2 θ – grzech 2 I. Służą one do wyrażania funkcji trygonometrycznych kątów podwójnych w postaci kątów pojedynczych.
Jak znaleźć wartości sinusów i cosinusów dla kątów w różnych ćwiartkach?
Znaki funkcji sinus i cosinus zależą od ćwiartki, w której leży kąt:
- Pierwsza ćwiartka: sin θ> 0 i cos θ> 0
- Druga ćwiartka: sin θ> 0 i cos θ <0
- Trzecia ćwiartka: sinθ <0 i cosθ <0
- Czwarta ćwiartka: sinθ 0
