Standardowa postać paraboli to y = ax2+ bx + c gdzie a, b i c są liczbami rzeczywistymi, a a nie jest równe zero. Parabolę definiuje się jako zbiór wszystkich punktów na płaszczyźnie, które są w jednakowej odległości od ustalonej linii i stałego punktu na płaszczyźnie.
W tym artykule szczegółowo zrozumiemy, czym jest parabola, standardowe równanie paraboli, powiązane przykłady i inne.
Spis treści
Co to jest parabola?
Parabola to przekrój stożkowy zdefiniowany jako zbiór wszystkich punktów w równej odległości od punktu zwanego ogniskiem i linii zwanej kierownicą. Standardowe równania paraboli zależą od jej orientacji (kierunku otwarcia) i położenia.
Równanie paraboli
Równanie paraboli można zapisać w postaci standardowej lub ogólnej i oba dodano poniżej:
Ogólne równania paraboli
Ogólne równanie paraboli to:
y = 4a(x – h) 2 + k
(Lub)
x = 4a(y – k) 2 + godz
Gdzie (h, k) jest wierzchołkiem paraboli.
Standardowe równania paraboli
Standardowe równanie paraboli to:
y = topór 2 + bx + c
(Lub)
x = jest 2 + przez + c
gdzie a nigdy nie może wynosić zero.
Części paraboli
Niektóre ważne terminy i części paraboli to:
- Centrum: Ognisko to stały punkt paraboli.
- Kierownica: Kierownica paraboli to linia prostopadła do osi paraboli.
- Akord ogniskowy: Cięciwa przechodząca przez ognisko paraboli, przecinająca parabolę w dwóch różnych punktach, nazywana jest cięciwą ogniskową.
- Odległość ogniskowa: Odległość ogniskowa to odległość punktu (x1, I1) na paraboli od ogniska.
- Prawa strona: Latus rectum to cięciwa ogniskowa, która przechodzi przez ognisko paraboli i jest prostopadła do osi paraboli. Długość latus rectum wynosi LL’ = 4a.
- Ekscentryczność: Stosunek odległości punktu od ogniska do jego odległości od kierownicy nazywa się mimośrodem (e). W przypadku paraboli mimośród jest równy 1, tj. e = 1.
Parabola ma cztery standardowe równania oparte na orientacji paraboli i jej osi. Każda parabola ma inną oś poprzeczną i oś sprzężoną.
| Równanie paraboli | Parabola | Wzory parametrów paraboli |
|---|---|---|
| I 2 = 4 oś | 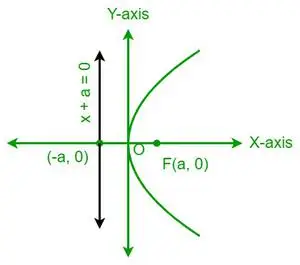 Parabola pozioma |
|
| I 2 = -4oś |  Parabola pozioma |
|
| X 2 = 4 dni |  Parabola pionowa |
|
| X 2 = -4 dni |  Parabola pionowa |
|
Poniżej znajdują się obserwacje wykonane na podstawie standardowej postaci równań paraboli:
- Parabola jest symetryczna względem swojej osi. Na przykład y2= 4ax jest symetryczne względem osi x, podczas gdy x2= 4ay jest symetryczne względem osi Y.
- Jeśli parabola jest symetryczna względem osi x, wówczas parabola otwiera się w prawo, jeśli współczynnik x jest dodatni, i w lewo, jeśli współczynnik x jest ujemny.
- Jeśli parabola jest symetryczna względem osi y, wówczas parabola otwiera się w górę, jeśli współczynnik y jest dodatni, i w dół, jeśli współczynnik y jest ujemny.
Poniżej znajdują się standardowe równania paraboli, gdy oś symetrii jest równoległa do osi x lub y, a wierzchołek nie znajduje się w początku układu współrzędnych.
| Równanie paraboli | Parabola | Wzory parametrów paraboli |
|---|---|---|
| (i – k)2= 4a(x – h) |  Parabola pozioma |
|
| (i – k)2= -4a(x – h) |  Parabola pozioma |
|
| (x – godz.)2= 4a(y – k) |  Parabola pionowa |
|
| (x – godz.)2= -4a(y – k) |  Parabola pionowa |
|
Równanie wyprowadzenia paraboli
Niech P będzie punktem paraboli o współrzędnych (x, y). Z definicji paraboli wynika, że odległość punktu P od ogniska (F) jest równa odległości tego samego punktu P od kierownicy paraboli. Rozważmy teraz punkt X na kierownicy, którego współrzędne to (-a, y).
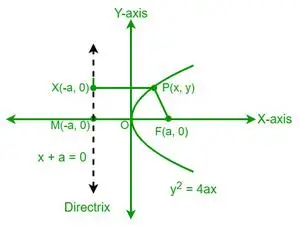
Z definicji mimośrodu paraboli mamy
e = PF/PX = 1
⇒ PF = PX
Współrzędne ogniska to (a, 0). Teraz, korzystając ze wzoru na odległość współrzędnych, możemy znaleźć odległość punktu P (x, y) od ogniska F (a, 0).
PF = √[(x – a)2+ (i – 0)2]
⇒ PF = √[(x – a)2+ i2] ------ (1)
Równanie kierownicy to x + a = 0. Aby znaleźć odległość PX, używamy wzoru na odległość prostopadłą.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Wiemy już, że PF = PX. Przyrównajmy więc równania (1) i (2).
√[(x – a)2+ i2] = (x + a)
Podnosząc do kwadratu po obu stronach otrzymujemy,
⇒ [(x – a)2+ i2] = (x + a)2
⇒ x2+ za2– 2 topór + y2= x2+ za2+ 2aks
⇒ i2– 2ax = 2ax
⇒ i2= 2 topór + 2 topór ⇒ I 2 = 4 oś
W ten sposób wyprowadziliśmy równanie paraboli. Podobnie możemy wyprowadzić standardowe równania pozostałych trzech paraboli.
- I2= -4oś
- X2= 4 dni
- X2= -4 dni
I 2 = 4ax i 2 = -4ax, x 2 = 4ay i x 2 = -4 dni są standardowymi równaniami paraboli.
Artykuły związane z parabolą:
- Równanie okręgu
- Równanie elipsy
- Równanie hiperboli
- Zastosowania paraboli w prawdziwym życiu
Przykłady równania paraboli
Przykład 1: Znajdź długość odbytnicy, ogniska i wierzchołka, jeśli równanie paraboli wynosi y 2 = 12x.
Rozwiązanie:
Dany,
Równanie paraboli to y2= 12x
Porównując dane równanie ze standardową formą y2= 4 oś
4a = 12
⇒ a = 12/4 = 3
Wiemy to,
Prawa strona paraboli = 4a = 4 (3) = 12
Teraz skupienie paraboli = (a, 0) = (3, 0)
Wierzchołek danej paraboli = (0, 0)
Przykład 2: Znajdź równanie paraboli, która jest symetryczna względem osi X i przechodzi przez punkt (-4, 5).
Rozwiązanie:
Dany,
Parabola jest symetryczna względem osi X i ma swój wierzchołek w początku.
Zatem równanie może mieć postać y2= 4ax lub y2= -4ax, gdzie znak zależy od tego, czy parabola otwiera się w lewą, czy w prawą stronę.
Parabola musi otwierać się w lewo, ponieważ przechodzi przez (-4, 5), które leży w drugiej ćwiartce.
Zatem równanie będzie wyglądało następująco: y2= -4oś
Podstawiając (-4, 5) do powyższego równania,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Zatem równanie paraboli wygląda następująco: y2= -4(25/16)x (lub) 4 lata2= -25x.
Przykład 3: Znajdź współrzędne ogniska, osi, równanie kierownicy i latus rectum paraboli x 2 = 16 lat.
Rozwiązanie:
Dany,
Równanie paraboli to: x2= 16 lat
Porównując dane równanie ze standardową formą x2= 4 dni,
4a = 16 ⇒ a = 4
Współczynnik y jest dodatni, więc parabola otwiera się w górę.
Ponadto oś symetrii przebiega wzdłuż dodatniej osi Y.
Stąd,
Ognisko paraboli to (a, 0) = (4, 0).
Równanie kierownicy to y = -a, tj. y = -4 lub y + 4 = 0.
Długość latus rectum = 4a = 4(4) = 16.
Przykład 4: Znajdź długość odbytnicy, ogniska i wierzchołka, jeśli równanie paraboli wynosi 2(x-2) 2 + 16 = y.
Rozwiązanie:
Dany,
Równanie paraboli to 2(x-2)2+ 16 = i
Porównując podane równanie z ogólnym równaniem paraboli y = a(x – h)2+ k, otrzymujemy
a = 2
(h, k) = (2, 16)
Wiemy to,
Długość latus rectum paraboli = 4a
= 4(2) = 8
Teraz skoncentruj się = (a, 0) = (2, 0)
Teraz wierzchołek = (2, 16)
Przykład 5: Równanie paraboli to x 2 – 12x + 4y – 24 = 0, a następnie znajdź jego wierzchołek, ognisko i kierownicę.
Rozwiązanie:
Dany,
Równanie paraboli to x2– 12x + 4 lata – 24 = 0
⇒ x2– 12x + 36 – 36 + 4 lata – 24 = 0
⇒ (x – 6)2+ 4 lata – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Otrzymane równanie ma postać (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Zatem wierzchołek = (h, k) = (6, – 15)
Ostrość = (h, k – a) = (6, -15-1) = (6, -16)
Równanie kierownicy to y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Często zadawane pytania dotyczące równania paraboli
Jak znaleźć równanie standardowe paraboli?
Standardową formą paraboli jest y2= 4ax lub x2= 4 dni.
Jakie jest równanie normalne paraboli?
Równanie normalnej do paraboli y2= 4ax z nachyleniem m wyraża się wzorem: y = mx – 2 w nocy – rano 3
Jak znaleźć wierzchołek paraboli?
Dla danej paraboli: y = ax2+ bx + c jego wierzchołek można znaleźć korzystając ze wzoru x = − b/2a. Podstaw tę wartość x z powrotem do równania, aby znaleźć odpowiednią współrzędną y.
przykładowe drzewo wyszukiwania binarnego
