Można zmierzyć trzy wymiary: długość, szerokość i wysokość dowolnego obiektu, który można zobaczyć lub dotknąć. Istnieją pewne wymiary naszego domu, w którym żyjemy. Prostokątny ekran/monitor, na który patrzysz, ma szerokość i szerokość swojej długości. Dla każdej trójwymiarowej struktury geometrycznej mierzone jest pole powierzchni i objętość.
Obszar objęty powierzchnią obiektu to powierzchnia dowolnego obiektu. Natomiast ilość miejsca dostępnego w obiekcie to objętość.
Spis treści
- Powierzchnia
- Całkowita powierzchnia
- Powierzchnia zakrzywiona/powierzchnia boczna
- Tom
- Przykłady dotyczące powierzchni i objętości
- Często zadawane pytania dotyczące wzorów na powierzchnię i objętość
Powierzchnia
Pole powierzchni i objętość można obliczyć dla dowolnego trójwymiarowego (3D) kształtu geometrycznego. Powierzchnia dowolnego obszaru to obszar zajmowany przez powierzchnię obiektu. Objętość to ilość miejsca dostępnego w obiekcie. Mamy różne rodzaje kształtów, takie jak półkula, kula, sześcian, prostopadłościan, walec itp. Wszystkie trójwymiarowe kształty mają powierzchnię i objętość. Ale dwuwymiarowe kształty, takie jak kwadraty, prostokąty, trójkąty, koła itp.
Tutaj w dwuwymiarze możemy zmierzyć jedynie powierzchnię. Obszar zajmowany przez obiekt trójwymiarowy przez jego zewnętrzną powierzchnię nazywany jest polem powierzchni. Mierzy się ją w jednostkach kwadratowych.
Obszar ten jest dwojakiego rodzaju:
- Całkowita powierzchnia
- Powierzchnia zakrzywiona/powierzchnia boczna
Całkowita powierzchnia
Obszar obejmujący podstawę(y) i zakrzywioną część odpowiada całkowitej powierzchni. Jest to wielkość obszaru zawartego w powierzchni obiektu. Jeśli forma ma zakrzywioną podstawę i powierzchnię, suma dwóch obszarów będzie całkowitym obszarem. Powierzchnię całkowitą można zdefiniować jako całkowitą powierzchnię zajmowaną przez obiekt, łącznie z jego podstawą i zakrzywioną częścią. Jeśli obiekt ma zarówno podstawę, jak i zakrzywioną powierzchnię, wówczas całkowite pole powierzchni będzie równe sumie podstawy i zakrzywionej powierzchni.
- Powierzchnia całkowita to całkowita powierzchnia zajmowana przez obiekt.
- Weźmy na przykład prostopadłościan, który ma 6 ścian, 12 krawędzi i 8 wierzchołków.
Całkowita powierzchnia = powierzchnia podstawowa + powierzchnia zakrzywiona
rokmiesiąc
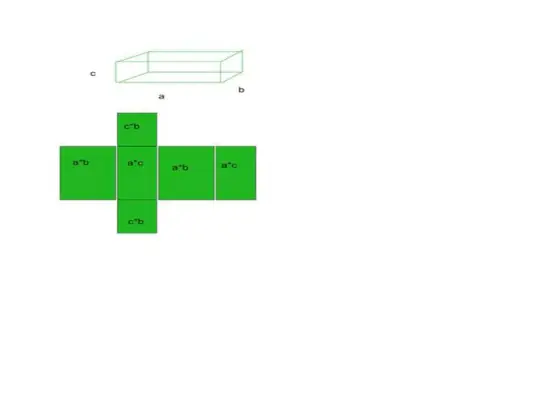
- Suma wszystkich tych 6 obszarów będzie naszą całkowitą powierzchnią danego kształtu
Przykład:
Poniżej podano prostopadłościan o wymiarach podanych jako długość = 8 cm, szerokość = 4 cm i wysokość = 6 cm. Znajdź TSA prostopadłościanu
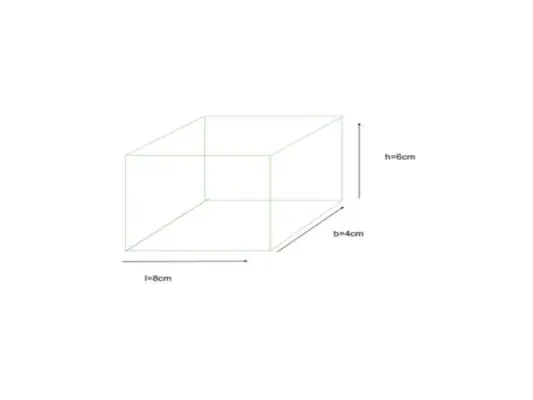
dane l = 8 cm, b = 4 cm, h = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA prostopadłościanu wynosi 208 cm.
Powierzchnia zakrzywiona/powierzchnia boczna
Zakrzywiona powierzchnia, z wyjątkiem jej środka, odpowiada powierzchni tylko zakrzywionej części kształtu (kształtów). W przypadku kształtów takich jak stożek często nazywa się to polem powierzchni bocznej. Pole powierzchni bocznej można zdefiniować jako obszar obejmujący wyłącznie zakrzywioną powierzchnię obiektu lub powierzchnię boczną obiektu, wykluczając powierzchnię bazową obiektu. Powierzchnia boczna jest również znana jako powierzchnia zakrzywiona.
Większość kształtów lub obiektów odnosi się do zakrzywionej powierzchni, kształt lub obiektowy cylinder odnosi się do niej jako do powierzchni bocznej. W uproszczeniu obszar, który jest dla nas widoczny, nazywany jest powierzchnią boczną. Rozważmy na przykład cylinder pokazany na poniższym rysunku.
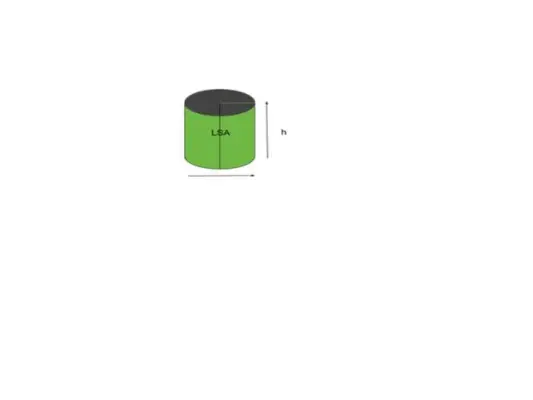
Tom
Objętość to ilość miejsca w określonym obiekcie 3D. Całkowita ilość przestrzeni zajmowanej przez przedmiot lub substancję nazywana jest objętością. Mierzy się go w jednostkach sześciennych.
Wzory powierzchni i objętości
Podana tabela zawiera powierzchnię całkowitą, powierzchnię zakrzywioną/powierzchnię boczną oraz objętość o różnych kształtach.
| Nazwa kształtu | Zakrzywiona powierzchnia | Całkowita powierzchnia | Tom |
|---|---|---|---|
| Prostopadłościan | 2h(l + b) | 2(lb + bh + hl) | l * b * godz |
| Sześcian | 4a2 | 6a2 | A3 |
| Cylinder | 2πrh | 2π(r + h) | πr2H |
| Kula | 4πr2 obudowa przełącznika Java | 4πr2 | 4/3π r3 |
| Stożek | πrl | πr(r + l) | 1/3π r2H |
| Półkula | 2pr2 | 3πr2 | 2/3π r3 |
Czytaj więcej:
- Powierzchnia piramidy
- Powierzchnia cylindra
- Powierzchnia półkuli
- Powierzchnia kuli
- Powierzchnia prostopadłościanu
Przykłady dotyczące powierzchni i objętości
Przykład 1: 2 kostki o objętości 512 cm każda 3 są połączone koniec z końcem. Znajdź pole powierzchni powstałego prostopadłościanu?
Rozwiązanie:
Dany,
Objętość (V) każdego sześcianu wynosi = 512 cm3
możemy teraz zasugerować, że a3= 512cm3
∴ Bok sześcianu, czyli a = 8 cm
Teraz szerokość i długość powstałego prostopadłościanu będzie wynosić 8 cm, a jego wysokość będzie wynosić 16 cm.
Zatem pole powierzchni prostopadłościanu (TSA) = 2(lb + bh + lh)
Teraz, wstawiając wartości, otrzymujemy,
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Stąd TSA prostopadłościanu = 640 cm 2
Przykład 2: Mamy świecę cylindryczną o średnicy 14 cm i długości 2 cm. Topi się, tworząc prostopadłościenną świecę o wymiarach 7 cm × 11 cm × 1 cm. Ile świec prostopadłościennych można zdobyć?
Rozwiązanie:
Wymiary świecy cylindrycznej:
Promień świecy cylindrycznej = 14/2 cm = 7 cm
Wysokość/Grubość=2 cm
Objętość jednej świecy cylindrycznej = πr2h = π x 7 x 7 x (2) cm3= 308cm3.
Objętość prostopadłościanu świeca = 7 x 11 x 1 = 77 cm3
Zatem liczba świec prostopadłościennych = Objętość świecy prostopadłościennej/Objętość jednej świecy cylindrycznej = 308/77 = 4
Stąd możemy otrzymać 4 świece w kształcie prostopadłościanu.
Przykład 3: Kobieta chce zbudować kulistą kulkę z gliny, której promień jest równy promieniowi bransoletki, którą nosi. Biorąc pod uwagę, że bransoletka ma okrągły kształt, chce również, aby powierzchnia bransoletki była równa objętości kuli. Dowiedz się, jaki jest promień bransoletki, którą nosi?
Rozwiązanie:
Niech r będzie promieniem bransolety i kuli,
Ustaliliśmy, że objętość kuli jest równa polu bransolety:
Stąd,
πr2= 4/3 πr3
⇒ r = 3/4
Zatem promień bransoletki wynosi 3/4 jednostki.
Przykład 4: Założono, że wysokość skosu prawego okrągłego stożka wynosi 25 cm, a jego wysokość wynosi 24 cm. Znajdź zakrzywioną powierzchnię stożka?
Rozwiązanie:
Wzór na zakrzywioną powierzchnię stożka to πrl. Gdzie r jest promieniem stożka, a l jest wysokością nachylenia stożka.
Tutaj stożek jest prawym okrągłym stożkiem.
Zatem promień stożka będzie wynosić:
r= sqrt{l^2 – h^2}
numer Armstronga=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Teraz obliczamy zakrzywioną powierzchnię:
Wymagana powierzchnia = (22/7) * 7 * 25 = 550 cm2
Stąd zakrzywiona powierzchnia stożka wynosi 550 cm 2 .
Przykład 5: Znajdź pole powierzchni bocznej walca o promieniu podstawy 6 cali i wysokości 14 cali.
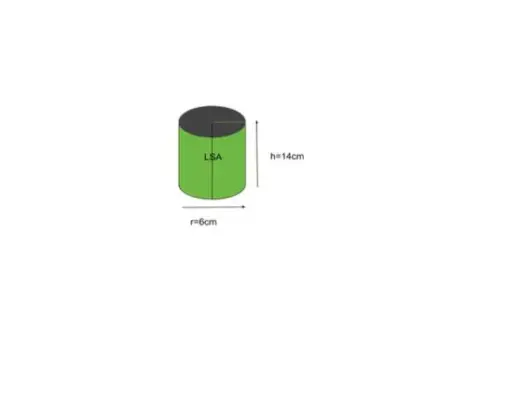
Rozwiązanie:
Dany promień r = 6, wysokość h = 14
LSA = 2ƒrh
= 2 * á * 6 * 14
= 168∏
= 527 787
= 528.
LSA danego cylindra wynosi 528cm .
Ćwicz pytanie dotyczące pól powierzchni i objętości
Różny Ćwicz pytania dotyczące powierzchni i objętości formuły to:
Pytanie 1. Znajdź pole powierzchni sześcianu o długości boku 5 centymetrów.
Pytanie 2. Oblicz objętość kuli o promieniu 3 metrów.
Pytanie 3. Oblicz całkowitą powierzchnię walca o promieniu 4 centymetrów i wysokości 8 centymetrów.
Pytanie 4. Znajdź objętość stożka o promieniu 6 cali i wysokości 10 cali.
Pytanie 5. Oblicz pole powierzchni prostopadłościanu o długości 7 metrów, szerokości 4 metrów i wysokości 6 metrów.
Często zadawane pytania dotyczące wzorów na powierzchnię i objętość
Jakie są wzory na pole powierzchni i objętość?
W powyższym artykule dodano różne wzory na powierzchnię i objętość.
Jaki jest wzór na objętość powierzchni klasy 10?
Wzór na pole powierzchni i klasę objętości 10 zawiera:
| Nazwa kształtu | Zakrzywiona powierzchnia | Całkowita powierzchnia | Tom |
|---|---|---|---|
| Prostopadłościan Java dołącz ciąg | 2h(l + b) | 2(lb + bh + hl) | l × b × wys |
| Sześcian | 4a2 | 6a2 | A3 |
| Cylinder | 2πrh | 2π(r + h) | πr2H |
| Kula | 4πr2 | 4πr2 | 4/3π r3 |
| Stożek | πrl | πr(r + l) | 1/3π r2H |
| Półkula | 2pr2 | 3πr2 | 2/3π r3 |
Jaki jest wzór prostopadłościanu na pole powierzchni i objętość?
- Powierzchnia prostopadłościanu = 2 (lb + bh + hl)
- Objętość prostopadłościanu = l × b × h
Co to jest powierzchnia i objętość?
Pole powierzchni to obszar wszystkich powierzchni bryły, a jej objętość to przestrzeń zajmowana przez sloid.
