The Złożoność czasu sortowania przez scalanie O(n log n) w obu przeciętny I najgorsze przypadki . Złożoność przestrzeni Sortowanie przez scalanie Jest NA) . 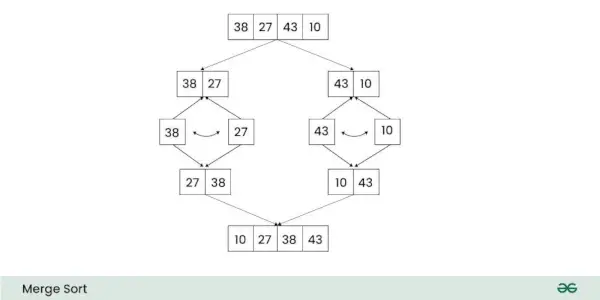
| Aspekt | Złożoność |
|---|---|
| Złożoność czasu | O(n log n) |
| Złożoność przestrzeni | NA) |
Analiza złożoności czasowej sortowania przez scalanie:
Rozważ następującą terminologię:
T(k) = czas potrzebny na posortowanie k elementów
M(k) = czas potrzebny na połączenie k elementów
Zatem można to napisać
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + stała * Nstos w Javie
Te elementy N/2 są dalej podzielone na dwie połowy. Więc,
T(N) = 2 * [2 * T(N/4) + stała * N/2] + stała * N
= 4 * T(N/4) + 2 * N * stała
. . .
= 2k*T(N/2k) + k * N * stała
Można go dzielić maksymalnie, aż pozostanie jeden element. Zatem N/2k= 1. k = log 2 N
jsp
T(N) = N * T(1) + N * log2N * stała
= N + N * log2N
Dlatego złożoność czasowa jest O(N * log 2 N) .
Zatem w najlepszym, najgorszym i przeciętnym przypadku złożoność czasowa jest taka sama.
Analiza złożoności przestrzeni sortowania przez scalanie:
Sortowanie przez scalanie ma złożoność przestrzeni z NA) . Dzieje się tak, ponieważ używa pomocniczej tablicy rozmiarów N aby połączyć posortowane połówki tablicy wejściowej. Tablica pomocnicza służy do przechowywania połączonego wyniku, a tablica wejściowa jest nadpisywana posortowanym wynikiem.
