Trapez w matematyce: Trapez to wielokąt mający cztery boki, czyli czworokąt. Trapez pochodzi od greckiego słowa trapez, które oznacza stół. Jest to złożony czworokąt. Trapez to specjalny czworokąt, który ma tylko jedną parę równoległych boków. Trapez to dwuwymiarowy kształt, który wygląda jak stół.
Trapez ma cztery boki i cztery wierzchołki. Kształt trapezu widzimy w naszym codziennym życiu i jest to jeden z najczęstszych kształtów. W tym artykule dowiemy się o czym jest trapez w matematyce, jego właściwości, wzory, przykłady i rodzaje trapezu, wraz z niektórymi jego rozwiązanymi przykładami.
Spis treści
- Co to jest trapez w matematyce?
- Rodzaje trapezu
- Nieregularny trapez
- Właściwości trapezu
- Formuła trapezu
- Obszar wzoru trapezu
- Obwód wzoru trapezu
- Różnica między trapezem a trapezem
- Kąty trapezu
- Przekątna trapezu
- Przykłady trapezów
Co to jest trapez w matematyce?
Trapez to dwuwymiarowy czworobok o kształcie zamkniętym, mający parę równoległych przeciwnych boków. Równoległe boki trapezu nazywane są podstawami, a nierównoległe boki trapezu nazywane są nogami. Trapez ma cztery boki i cztery narożniki. A równoległobok nazywany jest także trapezem o dwóch równoległych bokach.
Definicja trapezu
Trapez to czworokąt (czterokątny wielokąt) mający co najmniej jedną parę równoległych boków. Te równoległe boki nazywane są podstawami trapezu, a pozostałe dwa boki nazywane są nogami, które niekoniecznie są równoległe.
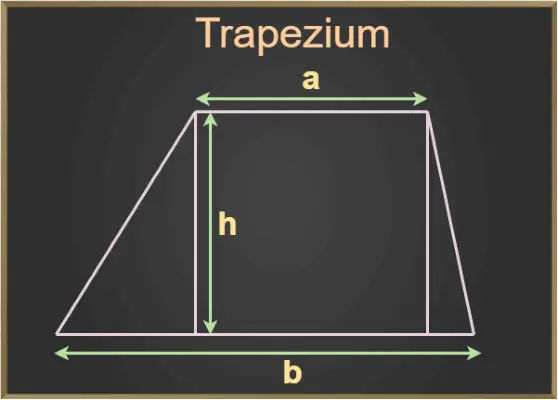
Na powyższym rysunku a i b to podstawy trapezu, a h to wysokość trapezu.
Kształt trapezu
Trapez jest czworoboczny tj. wielokąt z czterema bokami. Trapez ma cztery boki i parę przeciwległych boków równoległych do siebie. Kształt trapezu jest bardzo powszechny i w naszym codziennym życiu widzimy różne rzeczy podobne do trapezu. Niektóre obserwowane przez nas przykłady trapezu z życia wziętego to stoły, płytki, obrazy i inne w kształcie trapezu.
tylko nick
Rodzaje trapezu
Ze względu na boki i kąty trapez dzieli się na trzy typy:
- Trapez skalenowy
- Trapez równoramienny
- Prawy trapez

Trapez równoramienny
Trapez, który ma równe długości ramion, nazywa się trapezem równoramiennym, co oznacza, że w trapezie równoramiennym dwa nierównoległe boki są równe.
Trapez skalenowy
Trapez, w którym wszystkie boki nie są równe, nazywa się trapezem skalenowym. W trapezie skalenowym nie ma dwóch równych kątów.
Prawy trapez
Trapez, który ma parę kątów prostych sąsiadujących ze sobą, nazywany jest trapezem prawym.
Nieregularny trapez
Trapez ma jedną parę boków równoległych, a pozostałe dwa boki są nierównoległe. W trapezie foremnym pozostałe dwa nierównoległe boki są równe, natomiast w przypadku trapezu nieregularnego dwa przeciwległe boki nierównoległe są nierówne.
Właściwości trapezu
Istnieją różne właściwości trapezu, niektóre z nich są następujące:
- Boki równoległe: Trapez ma dwa równoległe boki, które nazywane są podstawami. Przykład: Boki AB i CD są do siebie równoległe, jak pokazano na rysunku.
- Boki nierównoległe: Nierównoległe boki trapezu nazywane są nogami, a ramiona trapezu nie są równej długości. Przykład: Boki AD i BC są bokami trapezu nierównoległymi.
- Wysokość lub wysokość: Prostopadła odległość między podstawami nazywana jest wysokością lub wysokością trapezu. Na powyższym schemacie h jest wysokością trapezu.
- Suma kątów
- Sąsiednie kąty wewnętrzne w trapezie sumują się do 180°. Przykład: Istnieją dwie pary kątów wspólnych wewnętrznych. Jedna para to ∠ A i ∠ D, podczas gdy druga para to ∠ B i ∠ C. Suma każdej pary kątów wewnętrznych wynosi 180°.
- Suma wszystkich kątów wewnętrznych w trapezie wynosi zawsze 360°. Przykład : Na rysunku ∠A+∠D wynosi 180°, a ∠B+∠C wynosi 180°. Zatem ∠A+∠D +∠B+∠C = 360°.
- Mediana: Mediana trapezu to odcinek łączący środki nóg. Mediana jest równoległa do podstaw, a jej długość jest średnią długości podstaw.
- Trapez ma dokładnie jedną parę przeciwległych boków, które są równoległe.
Formuła trapezu
Ważne wzory trapezu to:
- Powierzchnia trapezu = ½ (suma boków równoległych) × (odległość między bokami równoległymi)
- Obwód trapezu = Suma wszystkich czterech stron
Obszar wzoru trapezu
Trapez ma odpowiednio dwa równoległe boki a i b, a jego wysokość wynosi h.
Teraz pole trapezu można obliczyć, znajdując średnią podstaw i mnożąc wynik przez wysokość. Stąd,
Powierzchnia trapezu = ((a +b)/2) × godz
Gdzie,
- A I B są podstawami trapezu
- H jest Wysokość
Pole trapezu równoramiennego
Niech a i b będą długościami równoległych boków trapezu ABCD, gdzie a i b są podstawami trapezu oraz a>b.
Ponieważ jest to trapez równoramienny, c jest długością obu nierównoległych boków, a h jest wysokością trapezu.
Teraz AB = a, CD = b, BC = AD = c
W Trójkąt prostokątny , AED
Długość prostopadłej, h = √ (ok 2 – (a-b) 2 ) [za pomocą Twierdzenie Pitagorasa ]….(1)
Teraz,
Pole = ½ × suma boków równoległych × wysokość trapezu
Powierzchnia = ½ × (a+b) × godz
Używając równania (1)
Pole trapezu równoramiennego = 1/2 × [√(ok 2 – (a-b) 2 ) (a+b)]
Obwód wzoru trapezu
Obwód trapezu oblicza się, obliczając sumę wszystkich jego boków. Stąd,
Obwód trapezu = AB + BC + CD + AD
Gdzie, AB, BC, CD I OGŁOSZENIE są bokami trapezu
Obwód trapezu równoramiennego
Jeśli w trapezie równoramiennym a i b są długościami boków równoległych, tj. podstaw, a c jest długością dwóch równych, nierównoległych boków, wówczas obwód jest określony wzorem:
Obwód = a + b + 2c
Gdzie,
- A , B są podstawami trapezu
- C jest równą stroną trapezu
Różnica między trapezem a trapezem
Ogólnie rzecz biorąc, zarówno Trapez, jak i Trapezoid są takie same, ale różnica polega na ich kraju pochodzenia.
- Trapez ma pochodzenie brytyjskie, jest czworokątem i figurą dwuwymiarową, ma dokładnie jedną parę równoległych boków przeciwległych do siebie. W Indiach używamy brytyjskiego angielskiego, stąd używa się słowa Trapez.
- Trapez ma amerykańskie pochodzenie, jest także czworokątem czterobocznym z jedną parą równoległych boków przeciwległych do siebie. Boki równoległe to podstawy, a kolejne dwa nierównoległe boki nazywane są ramionami trapezu.
Kąty trapezu
Trapez jest czworokątem, a suma wszystkich kątów czworokąta wynosi 360 stopni. Zatem suma wszystkich kątów wewnętrznych trapezu wynosi 360 stopni.
Dla dowolnego trapezu foremnego, tj. Trapez, w którym nierównoległe boki są równe sąsiadującym kątom utworzonym między linią równoległą i linią nierównoległą, jest równy. Zatem suma tych dwóch kątów jest uzupełniająca.
Weźmy przykład na poparcie tej koncepcji dla trapezu równoramiennego ABCD, jeśli AB jest równoległe do CD i AD jest równe CD, wtedy wiemy, że ∠A = ∠B i ∠C = ∠D,
∠A + ∠B + ∠C + ∠D = 360°
Tutaj ∠A = ∠B i ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Podobnie (∠B + ∠D) = 180°
Przekątna trapezu
Trapez to szczególny rodzaj czworoboku; zatem trapez ma również dwie przekątne. Przekątne trapezu nie mają równych długości, w przeciwieństwie do niektórych innych czworokątów, takich jak prostokąty lub równoległoboki. Przekątne trapezu nie mają równych długości, a długości przekątnych zależą od długości podstaw i kątów trapezu.
Przykład: W przypadku trapezu równoramiennego ABCD kąt przy podstawie ∠A wynosi 80°, a następnie znajdź drugi kąt ∠C.
Wiemy, że dla trapezu równoramiennego ABCD,
(∠A + ∠C) = 180°
Biorąc pod uwagę, ∠A = 80°
narzędzie do wycinania w UbuntuTeraz 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Zatem wymagany kąt ∠C wynosi 100°
Wzory trapezu – powierzchnia i obwód trapezu
Wzory związane z trapezem podsumowano w poniższej tabeli:
| Nieruchomość | Formuła |
|---|---|
| Obszar | 1/2 × ( A + B ) × H |
| Powierzchnia (trapez równoramienny) | 1/2 × [√ (ok2– (a-b)2) (a+b)] |
| Obwód | A + B + C + D |
| Obwód (trapez równoramienny) | A + B + 2 C |
| Mediana | (A + b)/2 |
Ludzie czytali także:
- Romb
- Trójkąt
- Jaki jest wzór na znalezienie pola trapezu?
Przykłady trapezów
Przykład 1: Znajdź czwarty bok trapezu, jeśli pozostałe trzy boki mają długości 8 cm, 12 cm i 16 cm, a obwód wynosi 40 cm.
Rozwiązanie:
Obwód jest podawany jako suma wszystkich jego boków. Niech długość o nieznana będzie jednostkami „x”.
Obwód = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4cm
Zatem długość nieznanego boku wynosi 4 cm
Przykład 2: Trapez ma boki równoległe o długości 15 cm i 11 cm oraz boki nierównoległe o długości 5 cm każdy. Oblicz obwód tego trapez.
Rozwiązanie:
Jest to trapez równoramienny, ponieważ wyraźnie wspomniano, że nierównoległe boki o długości 5 cm każdy są równe.
Według trapezu równoramiennego, jeśli dwa nierównoległe boki trapezu mają tę samą długość, wówczas nazywa się go trapezem równoramiennym.
Dany,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Obwód = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Przykład 3: Znajdź obwód trapezu, którego boki mają długość 12 cm, 14 cm, 16 cm i 18 cm.
Rozwiązanie:
P = Suma wszystkich stron
P. = 12 + 14 + 16 + 18
P = 60 cm
Zatem obwód trapezu wynosi 60 cm
Przykład 4: Znajdź pole trapezu, którego suma boków równoległych wynosi 60 cm, a jego wysokość wynosi 10 cm.
Rozwiązanie:
Dany,
- Suma boków równoległych wynosi 60 cm
- wysokość, h = 10 cm
Pole trapezu, A = 1/2 × Suma boków równoległych × Odległość między bokami równoległymi
Zastępowanie podanych wartości,
Java mieszając do intA =1/2×60×10
A = 30×10
A = 300 cm2
Zatem pole trapezu = 300 cm2
Ćwicz problemy z trapezem w matematyce
1. Znajdź pole trapezu o podstawach 10 cm i 15 cm oraz wysokości 6 cm.
2. Trapez ma powierzchnię 54 metrów kwadratowych. Jeśli jedna z podstaw ma długość 12 metrów i wysokość 6 metrów, znajdź długość drugiej podstawy.
3. Oblicz obwód trapezu o podstawach 8 cm i 14 cm oraz nierównoległych bokach 5 cm i 7 cm.
4. Oblicz długość środkowego odcinka trapezu, którego podstawy mają długość 18 cm i 30 cm.
5. W trapezie równoramiennym kąty przy jednej podstawie wynoszą po 45 stopni. Znajdź miary kątów przy drugiej podstawie. Załóżmy, że trapez nie jest trapezem prostokątnym.
Podsumowanie – Trapez w matematyce
Trapez to czteroboczny wielokąt lub czworokąt, charakteryzujący się jedną parą równoległych boków zwanych podstawami, podczas gdy pozostałe dwa boki, zwane nogami, nie są równoległe. Powszechnie spotykany w przedmiotach codziennego użytku, takich jak stoły, trapez wyróżnia się swoimi właściwościami geometrycznymi: ma wysokość, która jest prostopadłą odległością między podstawami, oraz środkową, która łączy środki nierównoległych boków i jest równoległa do podstaw.
Pole trapezu oblicza się poprzez uśrednienie długości podstaw i pomnożenie przez wysokość, a jego obwód jest sumą wszystkich jego boków. Dzięki różnym klasyfikacjom, takim jak skalen, równoramienny i trapez prawy, każdy z unikalnymi właściwościami boków i kątów, trapezy mają fundamentalne znaczenie zarówno w zastosowaniach praktycznych, jak i teorii geometrycznej.
Często zadawane pytania dotyczące trapezu w matematyce
Jaki jest kształt trapezu?
Trapez to czworokąt, w którym para prostych jest zawsze równoległa. Przypomina kształtem stół. Jego nazwa pochodzi od greckiego słowa trapez, które oznacza stół.
Ile rodzajów trapezu?
Istnieją dwa rodzaje trapezu,
- Zwykły trapez: W którym druga para linii jest równa.
- Nieregularny trapez: W którym druga para linii nie jest równa.
Ile boków równoległych ma trapez?
Wiemy, że trapez jest czworokątem z jedną parą boków równoległych. Zatem trapez ma parę równoległych linii (boków).
Czy trapez można uznać za czworokąt?
A ma cztery boki, cztery wierzchołki i cztery kąty. Stąd można go uznać za czworokąt, suma wszystkich czterech kątów wewnętrznych trapezu wynosi 360 stopni.
Czy kwadrat można nazwać trapezem?
Trapez to czworokąt, który ma tylko jedną parę boków równoległych, a pozostałe dwa boki są nierównoległe. Ale w przypadku kwadratu ma on dwie pary równoległych boków, dlatego nie można go uznać za trapez.
Czy przekątne trapezu są zawsze równe?
Przekątne trapezu nie mogą być równe. W przypadku wielokąta foremnego przekątne są równe, ale w przypadku wielokąta nieregularnego nie jest to prawdą.
Jakie są właściwości trapezu?
5 właściwości trapezu to:
- W trapezie podstawy są do siebie równoległe.
- Trapez ma dodatkowe sąsiednie kąty.
- Tylko jedna para przeciwległych boków jest równoległa.
- Suma wszystkich kątów wewnętrznych w trapezie wynosi zawsze 360°.
- Linia łącząca środki nierównoległych boków jest zawsze równoległa do podstaw.
