WYNIK Z W STATYSTYKACH - NAUKA O DANYCH

Wynik Z w statystykach jest miarą tego, ile odchyleń standardowych ma punkt danych od średniej rozkładu. Znajdźmy wynik z w statystykach. Wartość Z wynosząca 0 wskazuje, że wynik punktu danych jest taki sam, jak wynik średni. Dodatni wynik z wskazuje, że punkt danych jest powyżej średniej, natomiast ujemny wynik z wskazuje, że punkt danych jest poniżej średniej.

Wzór na obliczenie wyniku Z jest następujący: z = (x – μ)/ p

Gdzie:

X: jest wartością testową
M: jest środkiem
Na: jest wartością standardową

W tym artykule omówimy następujące koncepcje:

Spis treści

Co to jest Z-Score?
Jak obliczyć Z-Score?
Charakterystyka Z-Score
Oblicz wartości odstające, korzystając z wartości Z-Score
Implementacja Z-Score w Pythonie
Zastosowanie Z-Score
Wyniki Z a odchylenie standardowe
Dlaczego wyniki Z nazywane są wynikami standardowymi?

Co to jest Z-Score?

Wynik Z, znany również jako wynik standardowy, informuje nas o odchyleniu punktu danych od średniej, wyrażając go w postaci odchyleń standardowych powyżej lub poniżej średniej. Daje nam wyobrażenie o tym, jak daleko punkt danych znajduje się od średniej. Dlatego też wynik Z jest mierzony jako odchylenie standardowe od średniej. Na przykład wynik Z wynoszący 2 oznacza, że wartość jest oddalona o 2 odchylenia standardowe od średniej. Aby użyć wyniku z, musimy znać średnią populacji (μ), a także odchylenie standardowe populacji (σ).

Wzór na wynik Z

Wynik Z można obliczyć za pomocą następującego wzoru.

z = (X – μ) / p

Gdzie,

z = Wynik Z
X = Wartość elementu
μ = średnia populacji
σ = odchylenie standardowe populacji

Jak obliczyć Z-Score?

Otrzymujemy średnią populacji (μ), odchylenie standardowe populacji (σ) i wartość zaobserwowaną (x) w opisie problemu, zastępując ją tą samą w równaniu Z-score, co daje nam wartość Z-Score. W zależności od tego, czy dany Z-Score jest dodatni czy ujemny, możemy go użyć dodatnia tabela Z Lub ujemna tabela Z dostępne w Internecie lub na odwrocie podręcznika do statystyki w załączniku.

Przykład 1:

Przystępujesz do egzaminu GATE i zdobywasz 500 punktów. Średni wynik w GATE wynosi 390, a odchylenie standardowe 45. Jak dobrze wypadłeś w teście w porównaniu do przeciętnego zdającego?

wyłącz tryb programisty

Rozwiązanie:

Poniższe dane są łatwo dostępne w powyższym pytaniu

Surowy wynik/obserwowana wartość = X = 500

Średni wynik = μ = 390

Odchylenie standardowe = σ = 45

Stosując wzór na wynik z,

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2.44

spróbuj złapać w Javie

Oznacza to, że Twój wynik Z wynosi 2,44 .

Ponieważ wynik Z jest dodatni i wynosi 2,44, skorzystamy z dodatniej tabeli Z.

Teraz przyjrzyjmy się Tabela Z (CC-BY), aby dowiedzieć się, jak dobrze wypadłeś w porównaniu z innymi zdającymi.

Postępuj zgodnie z poniższą instrukcją, aby znaleźć prawdopodobieństwo z tabeli.

Tutaj, z-score = 2,44, Który I wskazuje, że punkt danych znajduje się 2,44 odchylenia standardowego powyżej średniej.

Najpierw zmapuj dwie pierwsze cyfry 2,4 na osi Y.
Następnie wzdłuż osi X mapa 0.04
Połącz obie osie. Przecięcie tych dwóch zapewni skumulowane prawdopodobieństwo powiązane z wartością Z-score, której szukasz

[To prawdopodobieństwo reprezentuje obszar pod standardową krzywą normalną na lewo od wyniku Z]

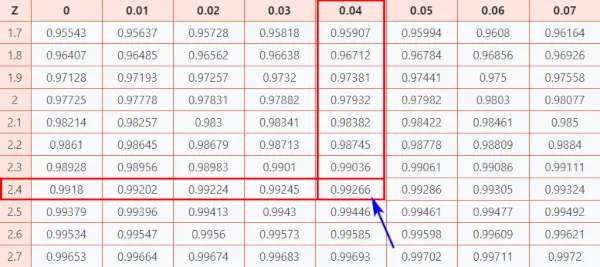
Tabela rozkładu normalnego

W rezultacie otrzymasz ostateczną wartość, która jest 0,99266 .

Teraz musimy porównać, jak nasz pierwotny wynik 500 w badaniu GATE ma się do średniego wyniku partii. Aby to zrobić, musimy przeliczyć skumulowane prawdopodobieństwo powiązane z wynikiem Z na wartość procentową.

0,99266 × 100 = 99,266%

Na koniec możesz powiedzieć, że spisałeś się lepiej niż prawie 99% innych zdających.

Przykład 2 : Jakie jest prawdopodobieństwo, że uczeń uzyska wynik pomiędzy 350 a 400 (przy średnim wyniku μ wynoszącym 390 i odchyleniu standardowym σ wynoszącym 45)?

Rozwiązanie:

Wynik minimalny = X₁= 350

Maksymalny wynik = X₂= 400

Stosując wzór na wynik z,

z₁= (X1 – m) / str

z₁= (350 – 390) / 45

z₁= -40 / 45 = -0,88

z₂= (X₂- poseł

z2 = (400 – 390) / 45

z₂= 10 / 45 = 0,22
wzorce programowania java

Ponieważ z1 jest ujemne, będziemy musieli przyjrzeć się wartości ujemnej Tabela Z i znajdź, że skumulowane prawdopodobieństwo p1, czyli pierwsze prawdopodobieństwo, wynosi: 0,18943 .

z₂jest dodatnia, więc używamy dodatniej tabeli Z, która daje skumulowane prawdopodobieństwo p₂z 0,58706 .

Ostateczne prawdopodobieństwo oblicza się odejmując p1 od p₂:

p = p₂- P₁

p = 0,58706 – 0,18943 = 0,39763

Prawdopodobieństwo, że uczeń uzyska wynik pomiędzy 350 a 400 wynosi: 39,763% (0,39763 * 100).

Charakterystyka Z-Score

Wielkość wyniku Z odzwierciedla odległość punktu danych od średniej w kategoriach odchyleń standardowych.
Element posiadający wynik Z mniejszy niż 0 oznacza, że element jest mniejszy od średniej.
Wyniki Z pozwalają na porównanie punktów danych z różnych rozkładów.
Element posiadający wynik Z większy niż 0 oznacza, że element jest większy od średniej.
Element posiadający wynik Z równy 0 oznacza, że element jest równy średniej.
Element posiadający wynik z równy 1 oznacza, że element jest o 1 odchylenie standardowe większy od średniej; wynik z równy 2, 2 odchylenia standardowe większe od średniej i tak dalej.
Element posiadający wynik z równy -1 oznacza, że element jest o 1 odchylenie standardowe mniejszy od średniej; wynik z równy -2, 2 odchylenia standardowe mniejsze od średniej i tak dalej.
Jeśli liczba elementów w danym zestawie jest duża, wówczas około 68% elementów ma wartość z w przedziale od -1 do 1; około 95% ma wynik z pomiędzy -2 a 2; około 99% ma wynik z pomiędzy -3 a 3. Jest to znane jako reguła empiryczna i określa procent danych w ramach pewnych odchyleń standardowych od średniej w rozkładzie normalnym, jak pokazano na poniższym obrazku

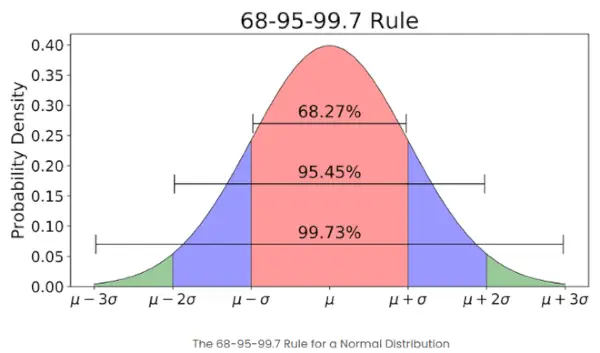
Empiryczna reguła rozkładu normalnego

Oblicz wartości odstające, korzystając z wartości Z-Score

Możemy obliczyć wartości odstające w danych, korzystając z wartości z-score punktów danych. Aby uwzględnić punkt danych odstających, należy wykonać następujące kroki:

Na początku zbieramy zbiór danych, w którym chcemy zobaczyć wartości odstające
Obliczymy średnią i odchylenie standardowe zbioru danych. Wartości te zostaną użyte do obliczenia wartości wyniku z każdego punktu danych.
Obliczymy wartość z-score dla każdego punktu danych. Wzór na obliczenie wartości z-score będzie taki sam jak
Z = frac{{X – mu}}{{sigma}}
gdzie X będzie punktem danych, μ jest średnią danych, a σ jest odchyleniem standardowym zbioru danych.
Określimy wartość odcięcia dla wyniku Z, po przekroczeniu której punkt danych będzie można uznać za wartość odstającą. Ta wartość odcięcia jest hiperparametrem, o którym decydujemy w zależności od naszego projektu.
Punkt danych, którego wartość z-score jest większa niż 3, oznacza, że punkt danych nie należy do punktu 99,73% zbioru danych.
Każdy punkt danych, którego wynik Z jest większy niż ustalona wartość odcięcia, zostanie uznany za wartość odstającą.

Sprawdzać: Wynik Z dla wykrywania wartości odstających

Implementacja Z-Score w Pythonie

Możemy użyć Pythona do obliczenia wartości Z-score punktów danych w zbiorze danych. Do obliczenia średniej i odchylenia standardowego zbioru danych użyjemy także biblioteki numpy.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Wartości odstające w zbiorze danych to {wartości odstające}')>

Wyjście:

Wynik Z: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Wartości odstające w zbiorze danych to [150]

Zastosowanie Z-Score

Wskaźniki Z są często używane do skalowania funkcji w celu dostosowania różnych funkcji do wspólnej skali. Normalizowanie funkcji gwarantuje, że mają one zerową średnią i wariancję jednostkową, co może być korzystne w przypadku niektórych algorytmów uczenia maszynowego, zwłaszcza tych, które opierają się na miarach odległości.
Wyników Z można używać do identyfikowania wartości odstających w zbiorze danych. Punkty danych z wynikami Z przekraczającymi określony próg (zwykle 3 odchylenia standardowe od średniej) można uznać za wartości odstające.
Wyniki Z można wykorzystać w algorytmach wykrywania anomalii w celu zidentyfikowania przypadków, które znacznie odbiegają od oczekiwanego zachowania.
Wyniki Z można zastosować do przekształcenia rozkładów skośnych w bardziej normalne rozkłady.
Podczas pracy z modelami regresji można analizować wyniki Z reszt w celu sprawdzenia homoskedastyczności (stałej wariancji reszt).
Wyniki Z można wykorzystać w skalowaniu cech, sprawdzając ich odchylenia standardowe od średniej.

Wyniki Z a odchylenie standardowe

Wynik Z	Odchylenie standardowe
Przekształć surowe dane w znormalizowaną skalę.	Mierzy wielkość zmienności lub rozproszenia w zestawie wartości.
Ułatwia porównywanie wartości z różnych zbiorów danych, ponieważ usuwają oryginalne jednostki miary.	Odchylenie standardowe zachowuje oryginalne jednostki miary, przez co jest mniej przydatne do bezpośrednich porównań między zbiorami danych o różnych jednostkach.
Wskaż, jak daleko punkt danych znajduje się od średniej pod względem odchyleń standardowych, zapewniając miarę względnej pozycji punktu danych w rozkładzie	Wyrażone w tych samych jednostkach, co dane oryginalne, stanowiące bezwzględną miarę rozproszenia wartości wokół średniej

Sprawdzać: Tabela wyników Z

Dlaczego wyniki Z nazywane są wynikami standardowymi?

Wyniki Z są również nazywane wynikami standardowymi, ponieważ standaryzują wartość zmiennej losowej. Oznacza to, że lista wyników standaryzowanych ma średnią 0 i odchylenie standardowe 1,0. Wyniki Z pozwalają również na porównanie wyników dla różnych rodzajów zmiennych. Dzieje się tak, ponieważ używają pozycji względnej do zrównywania wyników różnych zmiennych lub rozkładów.

Wyniki Z są często używane do porównania zmiennej ze standardowym rozkładem normalnym (przy μ = 0 i σ = 1).

Z-Score w statystykach – często zadawane pytania

Jakie jest znaczenie dodatnich i ujemnych wyników Z?

Dodatnie wyniki Z wskazują wartości powyżej średniej, podczas gdy ujemne wyniki Z wskazują wartości poniżej średniej. Znak odzwierciedla kierunek odchylenia od średniej.

Co oznacza wynik Z wynoszący 0?

Wynik Z wynoszący 0 wskazuje, że wartość punktu danych jest dokładnie równa średniej zbioru danych. Sugeruje to, że punkt danych nie znajduje się ani powyżej, ani poniżej średniej.

Jaka jest zasada 68-95-99,7 w odniesieniu do wyników Z?

Reguła 68-95-99,7, znana również jako Reguła empiryczna, stwierdza, że:
wyjątek nullpointer

Około 68% danych mieści się w granicach 1 odchylenia standardowego od średniej.
Około 95% mieści się w granicach 2 odchyleń standardowych.
Około 99,7% mieści się w granicach 3 odchyleń standardowych.

Czy wyniki Z można wykorzystać w przypadku rozkładów innych niż normalne?

Wyniki Z opierają się na założeniu, że dane mają rozkład normalny. Jednak w praktyce wyniki Z są korzystne w przypadku danych o rozkładzie normalnym. Chociaż wyniki Z można obliczyć dla dowolnego rozkładu, ich interpretacja staje się mniej wiarygodna i prosta w przypadku danych o rozkładzie normalnym.

Jak można zastosować Z-Scores w rzeczywistych sytuacjach?

Z-Scores mają różne zastosowania, np. w finansach do analizy portfela, edukacji do standardowych testów, zdrowiu do ocen klinicznych i nie tylko. Stanowią standaryzowaną miarę służącą do porównywania i interpretacji danych.