Zera wielomianu czy są to wartości rzeczywiste, urojone lub zespolone, gdy zostaną umieszczone w wielomianu zamiast zmiennej, wynik wyniesie zero (jak sama nazwa sugeruje również zero). Wielomiany służą do modelowania niektórych zjawisk fizycznych zachodzących w prawdziwym życiu, są bardzo przydatne w matematycznym opisie sytuacji.

Zera wielomianu to wszystkie wartości x, które sprawiają, że wielomian jest równy zero. Zera wielomianu mówią nam o punktach przecięcia x wykresu wielomianu. W tym artykule omówimy temat zera wielomianu, jak je znaleźć, twierdzenie o czynnikach itp.

Spis treści

• Co to są zera wielomianów?
• Zera wzoru wielomianu
• Jak znaleźć zero wielomianu?
• Dla wielomianu liniowego
• Dla wielomianu kwadratowego
• Dla wielomianu sześciennego
• Twierdzenie o czynnikach
• Zależność między zerami a współczynnikiem
• Zależność między zerami a współczynnikiem równania kwadratowego
• Zależność między zerami a współczynnikiem równania sześciennego
• Tworzenie równania z zerami wielomianu
• Zera na wykresie wielomianów
• Podstawowe twierdzenie algebry liniowej
• Wielość pierwiastka
• Artykuły związane z zerami wielomianów
• Przykładowe problemy dotyczące zer wielomianu
• Ćwicz problemy dotyczące zer wielomianu

Co to są zera wielomianów?

W przypadku wielomianu P(x) mówimy, że x = a jest zerem wielomianu, jeśli P(a) = 0, a wszystkie takie zera wielomianu są powszechnie nazywane zerami wielomianu. Rozważmy na przykład f(x) = 3x – 12. Teraz wstawmy x = 4 do wielomianu, tj. f(4) = 3×4 – 12 = 0. Zatem x = 4 jest zerem wielomianu f( x) = 3x – 12.

Przykład: Dla f(x) = x ³ – 6x ² + 11x – 6, czy x = 1 zero?

Rozwiązanie:

Aby sprawdzić, czy jeśli x = 1 jest zerem dla f(x) = x³– 6x²+ 11x – 6 lub nie, wstaw x = 1 do (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Zatem x = 1 jest zerem f(x).

Zera wzoru wielomianu

Dla wielomianu liniowego o postaci ax + b jego zero jest określone przez x = -b/a.

Dla wielomianu kwadratowego postaci ax²+ bx + c, jego zero jest określone przez x = {- b ± √D}/2a gdzie D jest dyskryminatorem określonym przez b²– 4ac.

Jak znaleźć zero wielomianu?

Możemy znaleźć zera wielomianu dla różnych typów wielomianów, korzystając z różnych metod omówionych poniżej.

• Dla wielomianu liniowego
• Dla wielomianu kwadratowego
• Dla wielomianu sześciennego

Dla wielomianu liniowego

W przypadku wielomianów liniowych znalezienie zera jest najłatwiejsze ze wszystkich. ponieważ istnieje tylko jedno zero i można to również obliczyć poprzez proste przegrupowanie wielomianu po wielomianu zrównującym do 0.

Na przykład znajdź zero dla wielomianu liniowego f(x) = 2x – 7.

Rozwiązanie:

Aby znaleźć zero f(x), przyrównaj f(x) do 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Dla wielomianu kwadratowego

Istnieją różne metody znajdowania pierwiastków lub zer wielomianu kwadratowego, takie jak dzielenie wyrazu środkowego, wzór kwadratowy znany również jako wzór Shree Dharacharya i uzupełnianie kwadratu, co jest nieco podobne do wzoru kwadratowego, ponieważ wzór kwadratowy pojawia się od uzupełnienia kwadratu ogólnego równania kwadratowego.

Dowiedz się więcej o rozwiązywanie równań kwadratowych lub wielomiany i sposoby ich rozwiązywania. Poniższe przykłady szczegółowo pokazują metodę znajdowania zer wielomianów kwadratowych.

Przykład 1: Znajdź zera dla P(x) = x ² + 2x – 15.

Odpowiedź:

X²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Przykład 2: Znajdź zera dla P(x) = x ² – 16x + 64.

Odpowiedź:

X²– 16x + 64 = 0

Porównanie z siekierą²+ bx + do = 0,

otrzymujemy a = 1, b = -16 i c = 64.

Zatem,

⇒ x = 8, 8

Dla wielomianu sześciennego

Aby znaleźć zera sześcienne, istnieje wiele sposobów, takich jak twierdzenie o pierwiastku racjonalnym i dzielenie przez długi czas. Jedna z metod znajdowania pierwiastków wielomianu sześciennego lub dowolnego wielomianu wyższego stopnia jest następująca:

Krok 1: Skorzystaj z twierdzenia o pierwiastkach racjonalnych, aby znaleźć możliwe pierwiastki. tj. jeśli wielomian ma pierwiastek wymierny, musi to być podział p/q, gdzie p jest stałą całkowitą, a q jest wiodącym współczynnikiem.

Krok 2: Po znalezieniu jednego pierwiastka podziel wielomian przez współczynnik utworzony przez ten pierwiastek, stosując dzielenie długie i zapisz wielomian jako iloczyn ilorazu i dywidendy.

Krok 3: Jeśli iloraz jest wyrażeniem kwadratowym, rozwiąż go metodami opisanymi powyżej dla wielomianów kwadratowych. Jeśli nie jest to wielomian stopnia 2, powtarzaj kroki 1 i 2, aż iloraz stanie się wielomianem stopnia 2.

Krok 4: Wynikiem kroku 3 są wymagane współczynniki i przyrównując współczynnik do 0, możemy znaleźć zera wielomianu.

Przykład: Znajdź zera wielomianu sześciennego p(x) = x ³ + 2x ² – 5x – 6.

Rozwiązanie:

p(x) = x³+ 2x²– 5x – 6

Ponieważ p/q = -6

Zgodnie z twierdzeniem o pierwiastku racjonalnym wszystkie możliwe pierwiastki racjonalne dwumianu są dzielnikami p/q.

Zatem dzielniki = ±1, ±2, ±3, ±6

x = -1, w p(x) otrzymujemy

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

sieciowy system operacyjny

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Zatem zgodnie z twierdzeniem o czynnikach x + 1 jest współczynnikiem p (x).

Zatem x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Dla zer p(x) = 0,

Zera p(x) to x = -1, x = 2 i x = -3.

Twierdzenie o czynnikach

Dla wielomianu P(x) twierdzenie o czynnikach stwierdza, że ​​jeśli x =a wynosi zero z P(X) iff x – a jest współczynnikiem P(x). tj. oba poniższe warunki powinny być spełnione.

• Jeśli a jest zerem P(x), to x−a będzie współczynnikiem P(x)
• Jeśli x−a jest współczynnikiem P(x), to a będzie zerem P(x)

Można to sprawdzić, patrząc na wcześniejsze przykłady. Twierdzenie o czynnikach może prowadzić do kilku interesujących wyników, które są następujące:

Wynik 1: Jeśli P(x) jest wielomianem stopnia n, a r jest zerem P(x), to P(x) można zapisać w następującej postaci:

P(x) = (x – r) Q(x)

Gdzie Q(x) jest wielomianem stopnia n-1 i można go znaleźć dzieląc P(x) przez (x – r).

Wynik 2: Jeśli P(x) = (x-r)Q(x) i x = t jest zerem Q(x), to x = t będzie również zerem P(x).

Aby zweryfikować powyższy fakt,

Powiedzmy, że t wynosi zero Q(x), co oznacza Q(t) = 0.

Wiemy, że r jest zerem wielomianu P(x), gdzie P(x) = (x – r) Q(x),

Musimy więc sprawdzić, czy x = t jest także zerem P(x), wstawmy x = t do P(x)

⇒ P(t) = (t – r) Q(t) = 0

Zatem x = t jest także zerem P(x).

Zatem udowodnione.

Zależność między zerami a współczynnikiem

Zależność między zerami a współczynnikiem równania kwadratowego i sześciennego omówiono poniżej.

Zależność między zerami a współczynnikiem równania kwadratowego

Dla równania kwadratowego postaci ax²+ bx + c = 0, jeśli dwa zera równania kwadratowego to α i β, to

• Suma pierwiastka = α + β = -b/a
• Iloczyn pierwiastków = α × β = c/a

Zależność między zerami a współczynnikiem równania sześciennego

Jeśli α, β i γ są pierwiastkami osi wielomianu sześciennego³+ bx²+ cx + d = 0, wówczas związek między jego zerami i współczynnikami jest następujący:

• a + b + do = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Tworzenie równania z zerami wielomianu

• W przypadku wielomianu kwadratowego z zerami α i β wielomian kwadratowy jest określony wzorem

X ² – (a + b)x + ab .

• W przypadku wielomianu sześciennego z trzema zerami α, β i γ wielomian sześcienny jest określony wzorem

X ³ – (a + b + do)x ² + (ab + ag + bg)x – abg

Zera na wykresie wielomianów

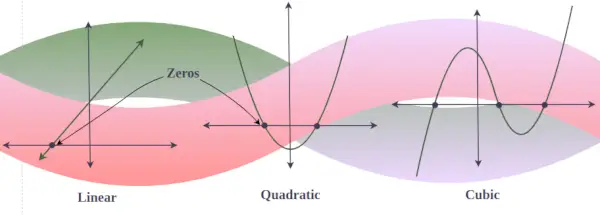
Na wykresie dowolnego wielomianu y = f(x) zera rzeczywiste to punkt, w którym wykres przecina lub styka się z osią x. (ponieważ wykres z urojonym zerem nigdy nie przecina osi x). Innymi słowy, jeśli istnieją 3 rzeczywiste rozwiązania wielomianu sześciennego, to wykres tego wielomianu sześciennego przecina oś x trzy razy, ale jeśli istnieje tylko jedno rzeczywiste rozwiązanie jakiegoś wielomianu sześciennego, to wykres ten przecina tylko oś x raz.

Podstawowe twierdzenie algebry liniowej

Jeśli P(x) jest wielomianem stopnia n, wówczas P(x) będzie miało dokładnie n zer, z których część może się powtarzać.

Oznacza to, że jeśli wylistujemy wszystkie zera i każde z nich wymienimy k razy, gdy k jest jego wielokrotnością. Na liście będziemy mieli dokładnie n liczb. Może to być przydatne, ponieważ może nam dać wyobrażenie o tym, ile zer powinno być w wielomianie. Możemy więc przestać szukać zer, gdy osiągniemy wymaganą liczbę zer.

Wielość pierwiastka

Załóżmy, że mamy wielomian P(x) = 0, który rozkłada się na czynniki:

P(x) = (x – r) ^k (x – a) ^M

Jeśli r jest zerem wielomianu, a wykładnik jego wyrazu, który dał pierwiastek, to k, to mówimy, że r ma wielość k . Często nazywane są zera z wielokrotnością 1 prosty zera i zera z wielokrotnością 2 nazywane są podwójnymi pierwiastkami wielomianu.

Przykład: P(x) to wielomian stopnia 5, który został dla Ciebie rozłożony na czynniki. Wymień korzenie i ich mnogość.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x-2) ³

Rozwiązanie:

Biorąc pod uwagę, P(x) = 5(x+1)²(x-2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Aby znaleźć zera, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Zauważ, że -1 występuje dwa razy jako zero, więc jego krotność wynosi 2, podczas gdy krotność zera 2 wynosi 3.

Artykuły związane z zerami wielomianów

• Wielomian
• Pierwiastki równania kwadratowego
• Wyrażenie algebraiczne

Przykładowe problemy dotyczące zer wielomianu

Problem 1: Biorąc pod uwagę, że x = 2 jest zerem P(x) = x ³ +2x ² −5x−6. Znajdź pozostałe dwa zera.

Rozwiązanie:

Z podstawowego twierdzenia, które badaliśmy wcześniej, możemy powiedzieć, że P(x) będzie miało 3 zera, ponieważ jest wielomianem trzech stopni. Jednym z nich jest x = 2.

Możemy więc przepisać P(x),

P(x) = (x – 2) Q(x)

Aby znaleźć pozostałe dwa zera, musimy znaleźć Q(x).

Q(x) można znaleźć dzieląc P(x) przez (x-2).

Po podzieleniu okazuje się, że Q(x) wynosi:

Q(x) = x²+ 4x + 3

Z tego można znaleźć pozostałe dwa zera,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Zatem pozostałe dwa zera to x = -1 i x = -3.

Zadanie 2: Biorąc pod uwagę, że x = r jest zerem wielomianu, znajdź pozostałe zera wielomianu.

P(x) = x ³ -6x ² −16x; r = −2

Rozwiązanie:

Wiemy, że x = -2 jest zerem,

Zatem P(x) można przepisać jako: P(x) = (x + 2) Q(x) {Korzystając z algorytmu dzielenia}

Teraz, aby znaleźć Q(x), robimy to samo, co w poprzednim pytaniu, dzielimy P(x) przez (x + 2).

Dostajemy,

Q(x) = x²– 8x

Teraz, aby znaleźć pozostałe dwa zera, rozłóż Q(x) na czynniki

Q(x) = x (x – 8) = 0

Zatem zera to x = 0, 8.

Zatem mamy trzy zera, x = -2, 0, 8.

Zadanie 3: Znajdź zera wielomianu, 4x ³ -3x ² -25x-6 = 0

Rozwiązanie:

Sztuczka rozwiązywania równań wielomianowych stopnia 3,

Znajdź najmniejszą liczbę całkowitą, która może dać wartość wielomianu 0, zacznij od 1,-1,2 i tak dalej…

stwierdzamy, że dla x = -2 otrzymujemy wartość wyrażenia równą zero.

Zatem jednym z pierwiastków jest -2.

Zgodnie z twierdzeniem o współczynniku, jeśli a jest jednym z zer wielomianu, stąd (x-a) jest współczynnikiem danego wielomianu.

Zatem po tym {x – (-2)} = (x+2) jest współczynnik pof powyżej wielomianu.

Otrzymujemy równanie kwadratowe i zera już tam są.

(4x²-11x-3)(x+2) = 0

Rozłóż na czynniki równanie kwadratowe,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Zadanie 4: Znajdź zera wielomianu, 4x ⁶ – 16x ⁴ = 0

Rozwiązanie:

Wielomian ma stopień do 6, zatem istnieje 6 zer wielomianu.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Zatem x= 0, 0, 0, 0, 2, -2

Zadanie 5: Znajdź miejsca zerowe funkcji wielomianowej f(x) = x ³ – 2x ² – 5x + 6

Rozwiązanie:

Aby znaleźć zera tego wielomianu, ustalamy f(x) = 0 i obliczamy x:

f(x) = x³– 2x²– 5x + 6 = 0

Ponieważ d/a = 6

Zgodnie z twierdzeniem o pierwiastku racjonalnym wszystkie możliwe racjonalne pierwiastki dwumianu to:

Dzielniki d/a = ±1, ±2, ±3, ±6

x = 1, w p(x) otrzymujemy

f(1) = (1)³– 2(1)²– 5 ust. 1 – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Zatem zgodnie z twierdzeniem o czynnikach x – 1 jest współczynnikiem p(x).

Zatem x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Dla zer p(x) = 0,

Zera p(x) to x = 1, x = -2 i x = 3.

Ćwicz problemy dotyczące zer wielomianu

1. Znajdź wszystkie zera wielomianu f(x) = x ³ – 6x ² + 11x – 6

2. Wyznacz wszystkie zera wielomianu g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Znajdź zera wielomianu h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Wyznacz wszystkie zera wielomianu p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Często zadawane pytania dotyczące zer wielomianu

Co to są zera wielomianu?

Te takie wartości rzeczywiste, dla wartości wielomianu wynosi 0, tj. jeśli p(x) jest wielomianem, a p(a) = 0, to x = a jest zerem p(x).

Jak znaleźć zera wielomianu?

Istnieją różne metody znajdowania zer dla różnych wielomianów, na przykład w przypadku kwadratowego rozlewania wyrazu środkowego i wzoru kwadratowego. Do liniowego, prostego przegrupowania zmiennych i do sześciennego używamy kombinacji twierdzenia o pierwiastku wymiernym, twierdzenia o długim dzieleniu, twierdzenia o czynnikach i twierdzenia o reszcie.

Czy wielomian może mieć więcej niż jedno zero?

Tak, wielomian może mieć więcej niż jedno zero, w rzeczywistości wielomian n stopni może mieć co najwyżej n zer rzeczywistych.

Jaka jest krotność zera wielomianu?

W procesie faktoryzacji jeden czynnik lub jedno zero wielomianu, a następnie pewna liczba razy czynnik lub zero, nazywa się to krotnością tego pierwiastka.

vlc pobieraj filmy z YouTube'a

Jakie jest podstawowe twierdzenie algebry?

Podstawowe twierdzenie o stanach algebry Jeśli P(x) jest wielomianem stopnia n, to P(x) będzie miało dokładnie n zer, z których część może się powtarzać.

Czy wielomian o stopniu n zawsze ma n pierwiastków rzeczywistych?

Nie, wielomian o stopniu n nie zawsze ma n pierwiastków rzeczywistych, ponieważ niektóre pierwiastki mogą być liczbami urojonymi lub zespolonymi.

Jaki jest stopień wielomianu zerowego?

Stopień zerowego wielomianu wynosi zero.