Kąt między dwoma wektorami to kąt między ich końcami i kąt ten można łatwo znaleźć za pomocą iloczynu krzyżowego i iloczynu skalarnego wzorów wektorowych. Kąt pomiędzy dwoma wektorami zawsze mieści się w przedziale od 0° do 180°.
W tym artykule dowiemy się szczegółowo o kącie między dwoma wektorami, definicji, wzorach i przykładach.
Co to jest kąt między dwoma wektorami?
Kąt między dwoma wektorami to kąt utworzony na przecięciu ich ogonów. Kąt między dwoma wektorami może być ostry, prosty lub rozwarty, w zależności od kierunku wektorów.
Kąt między dwoma wektorami wyznacza się za pomocą dwóch wzorów:
- Korzystanie z iloczynu skalarnego wektorów
- Korzystanie z iloczynu krzyżowego wektorów
Wyjaśniono to w poniższym wzorze.
Kąt między dwoma wzorami wektorów
Kąt między dwoma wektorami można łatwo i najczęściej znaleźć za pomocą iloczynu skalarnego wektorów.

Dwa wektory A i B
Produkt kropkowy A i B jest dana przez,
vec{A}.vec{B} = |A| |B| cosθ.
Specjalne przypadki
- Gdy kąt między wektorami wynosi 0 stopni.
Oznacza to, że θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Gdy kąt między wektorami wynosi 180 stopni.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Gdy kąt między wektorami wynosi 90 stopni.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Wzór na kąt między dwoma wektorami
Cosinus kąta między dwoma wektorami jest równy sumie iloczynu poszczególnych składników dwóch wektorów podzielonej przez iloczyn wielkości dwóch wektorów.
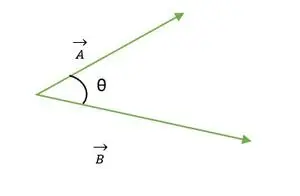
Dwa wektory A i B
cosθ=
θ= sałata-1
W formie kartezjańskiej
A = AXja + AIj + Azk
B= BXja + BIj + Bzk
sałata θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Właściwości produktu Dot
- Iloczyn skalarny jest przemienny
vec{A}.vec{B}=vec{B}.vec{A}
- Iloczyn kropkowy jest dystrybutywny
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})
Kąt między dwoma wektorami mieści się w przedziale 0 ≤ θ ≤ 180. Gdy ogony lub główki obu wektorów pokrywają się, wówczas obliczany jest kąt między wektorami.
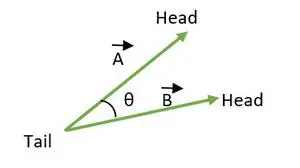
Ogon zbiegł się
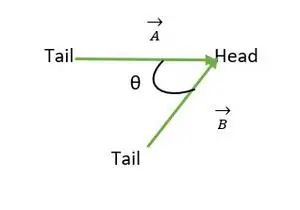
Głowa zbieżna
Przykładowe problemy Wzór kąta między dwoma wektorami
Zadanie 1: Znajdź kąt między wektorami (jeśli tworzą trójkąt równoboczny)
- wektory a i b
- wektory b i c
- wektory a i c
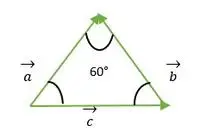
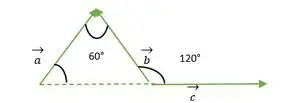
Trójkąt równoboczny utworzony przez wektor a, b, c
Rozwiązanie:
- wektory a i b
Dla wektorów a i b głowy obu wektorów pokrywają się, stąd kąt między wektorami a i b jest taki sam, jak kąt między dwoma bokami trójkąta równobocznego = 60°.
- wektory b i c:
Z powyższego rysunku widzimy, że głowa lub ogon wektora b i c nie pokrywają się ze sobą.
Tak więc, korzystając z właściwości: wektor pozostaje niezmieniony, jeśli jest przesyłany równolegle do siebie.
Wektor c jest przesunięty równolegle do siebie
Teraz widzimy, że ogony wektorów b i c pokrywają się ze sobą, a zatem są takie same, jak kąt zewnętrzny utworzony w trójkącie równobocznym = 120°.
- wektory a i c
Ogony a i c pokrywają się
Dla wektorów a i c ogony obu wektorów pokrywają się, stąd kąt między wektorem a i c jest równy kątowi między dwoma bokami trójkąta równobocznego = 60°.
Zadanie 2: Znajdź kąty między wektorami, jeśli tworzą one trójkąt prostokątny równoramienny.
- wektor aib
- wektor b i c
- wektory a i c
Rozwiązanie:
- wektor aib
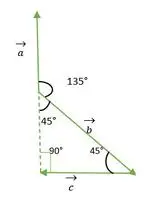
Trójkąt równoramienny prostokątny
Z powyższego rysunku widzimy, że głowa lub ogon wektora a i b nie pokrywają się ze sobą. Tak więc, korzystając z właściwości: wektor pozostaje niezmieniony, jeśli jest przesyłany równolegle do siebie.
wektor jest przesunięty równolegle do siebie
Teraz ogony wektorów a i b pokrywają się ze sobą i tworzą kąt równy kątowi zewnętrznemu trójkąta równoramiennego o kącie prostym = 135°.
- wektor b i c
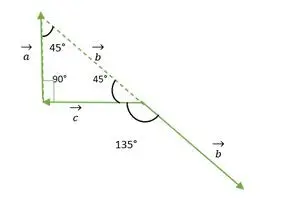
Trójkąt równoramienny prostokątny
Z powyższego rysunku wynika, że głowa lub ogony wektorów b i c nie pokrywają się ze sobą. Zatem, korzystając z tej właściwości, wektor pozostaje niezmieniony, jeśli jest przesyłany równolegle do siebie.
wektor b jest przesunięty równolegle do siebie
Teraz ogony wektorów b i c pokrywają się ze sobą i tworzą kąt równy kątowi zewnętrznemu trójkąta równoramiennego o kącie prostym = 135°.
- wektory a i c
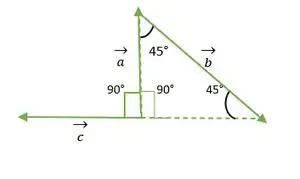
Trójkąt równoramienny prostokątny
Z powyższego rysunku wynika, że głowa lub ogony wektorów a i c nie pokrywają się ze sobą. Tak więc, korzystając z właściwości: wektor pozostaje niezmieniony, jeśli jest przesyłany równolegle do siebie.
wektor c jest przesuwany równolegle do siebie
Teraz ogony wektorów a i c pokrywają się i tworzą kąt równy kątowi prostemu trójkąta równoramiennego = 90°.
Zadanie 3: Znajdź kąt pomiędzy wektorami A = i + j + k i wektorem B = -2i – 2j – 2k.
Rozwiązanie:
Ze wzoru
A = AXja + AIj + Azk
B= BXja + BIj + Bzk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Tutaj, w zadanym pytaniu,
A= ja + jot + k
B= -2i -2j -2k
Zastępowanie wartości we wzorze
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} ⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
Zadanie 4: Znajdź kąt pomiędzy wektorem A = 3i + 4j i B = 2i + j
Rozwiązanie:
A = AXja + AIj + Azk
B = BXja + BIj + Bzk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Tutaj biorąc pod uwagę,
A= 3i + 4j + 0k
B= 2i + j + 0k
Podstawiając wartości we wzorze,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = sałata-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = sałata-1(
frac{2}{(sqrt{5})} )
Zadanie 5: Znajdź kąt pomiędzy wektorem A = i + j i wektorem B = j + k.
Rozwiązanie:
Ze wzoru
A = AXja + AIj + Azk
B = BXja + BIj + Bzk
Java len tablicycosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Tutaj, w zadanym pytaniu,
⇒ ZA = ja + jot
⇒ B = jot + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = sałata-1(1/2)
⇒ θ = 60°