WZÓR COTANGENS - TECHCODEVIEW.COM

Trygonometria jest ważną gałęzią matematyki zajmującą się zależnością między długościami boków i kątami trójkąta prostokątnego. Sinus, cosinus, tangens, cosecans, secans i cotangens to sześć stosunków lub funkcji trygonometrycznych. Gdzie stosunek trygonometryczny jest przedstawiany jako stosunek boków trójkąta prostokątnego.

sin θ = przeciwna strona/przeciwprostokątna
cos θ = sąsiedni bok/przeciwprostokątna
tan θ = strona przeciwna/strona sąsiednia
cosec θ = 1/sin θ = przeciwprostokątna/strona przeciwna
sec θ = 1/cos θ = przeciwprostokątna/przylegająca strona
łóżko θ = 1/tan θ = strona sąsiadująca/strona przeciwna

Wzór cotangensowy

Funkcja Cotangens jest funkcją odwrotną danej funkcji stycznej. Wartość kąta cotangens w trójkącie prostokątnym jest stosunkiem długości boku przylegającego do danego kąta do długości boku przeciwnego do danego kąta. Funkcję cotangens zapisujemy jako cot.

Trójkąt ABC

Teraz wzór cotangens na kąt θ to:

łóżeczko θ = (Strona sąsiednia)/(Strona przeciwna)

Funkcja cotangens jest dodatnia w pierwszej i trzeciej ćwiartce oraz ujemna w drugiej i czwartej ćwiartce.

łóżeczko (2π + θ) = łóżeczko θ (1^ulkwadrant)
łóżeczko (π – θ) = – łóżeczko θ (2^IIkwadrant)
łóżeczko (π + θ) = łóżeczko θ (3^{r & D}kwadrant)
łóżeczko (2π – θ) = – łóżeczko θ (4^tkwadrant)

Funkcja cotangens jest funkcją ujemną, ponieważ cotangens kąta ujemnego jest ujemną kotangensem kąta dodatniego.

łóżeczko (-θ) = – łóżeczko θ

Jeśli chodzi o funkcję styczną, funkcja cotangens jest zapisana jako:

łóżko θ = 1/opalenizna θ

(Lub)

łóżeczko θ = tan (90° – θ) (lub) tan (π/2 – θ)

Funkcję cotangens w postaci funkcji sinus i cosinus można zapisać jako:

łóżko θ = cos θ/sin θ

Wiemy, że łóżko θ = strona sąsiednia/strona przeciwna

Teraz podziel licznik i mianownik przez przeciwprostokątną

⇒ łóżko θ = (przylegająca strona/przeciwprostokątna) / (przeciwna strona/przeciwprostokątna)

Wiemy, że sin θ = przeciwna strona/przeciwprostokątna

cos θ = sąsiedni bok/przeciwprostokątna

Stąd łóżeczko θ = cos θ/sin θ
javascript po kliknięciu

Funkcję cotangens w postaci funkcji sinus można zapisać jako:

łóżko θ = (√1 – grzech ² i)/grzech i

Wiemy, że cos θ = cos θ/sin θ

Z tożsamości pitagorejskich mamy;

sałata²θ + grzech²θ = 1

⇒ cos θ = √1 – grzech²I

Stąd łóżeczko θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Funkcję cotangens w funkcji cosinus można zapisać jako:

łóżko θ = cos θ/(√1 -cos ² I)

Wiemy, że cos θ = cos θ/sin θ

Z tożsamości pitagorejskich mamy;

sałata²θ + grzech²θ = 1

sin θ = √1 – sałata²I

Stąd łóżeczko θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Funkcję cotangensa w postaci funkcji siecznych i cosekansowych można zapisać jako:

łóżko θ = cosec θ/s θ

Mamy, cos θ = cos θ/sin θ

Można to zapisać jako: cot θ = (1/sin θ) / (1/cos θ)

⇒ łóżko θ = cosec θ/s θ

Funkcję cotangens w funkcji cosecans można zapisać jako:

łóżko θ = √(cosec ² - 1)

Z tożsamości pitagorejskich mamy:

cosek²θ – łóżeczko²θ = 1

⇒ łóżeczko²θ = 1 – cosek²- 1

Stąd łóżeczko θ = √(cosec²- 1)

Funkcję cotangens w funkcji siecznej można zapisać jako:

łóżko θ = 1/(√ sek ² ja – 1)

Z tożsamości pitagorejskich mamy:

sek²θ – tak²θ = 1

tan θ = √ sek²ja – 1

Wiemy o tym, że łóżeczko θ = 1/tan θ

Stąd, łóżeczko θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Tabela współczynników trygonometrycznych

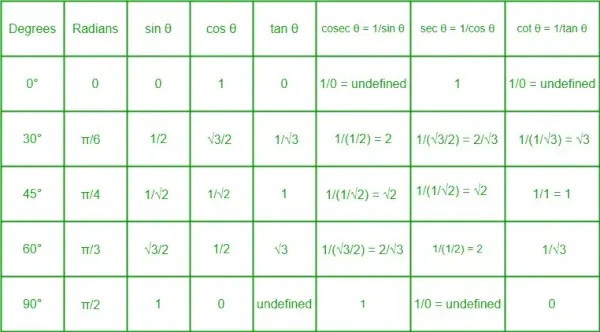
Tabela współczynników trygonometrycznych

Prawo Cotangensów lub Prawo Cotangensów

Prawo cotangensowe wygląda podobnie do prawa sinusoidalnego, ale tutaj dotyczy kątów połówkowych. Prawo kotangentów opisuje związek między długościami boków trójkąta a kotangami połówek trzech kątów. Rozważmy trójkąt ABC, gdzie a, b i c są długościami boków trójkąta.

Prawo kotangentów stwierdza, że:

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Gdzie s jest półobwodem trójkąta ABC, a r jest jego promieniem okręgu wpisanego w trójkąt.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Przykładowe problemy

Zadanie 1: Znajdź wartość łóżeczka θ, jeśli tg θ = 3/4.

Rozwiązanie:

Biorąc pod uwagę dane, tan θ = 3/4

Wiemy to, łóżko θ = 1/opalenizna θ

⇒ łóżko θ = 1/(3/4) = 4/3

Zatem łóżko θ = 4/3

Zadanie 2: Znajdź wartość łóżeczka α, sin α = 1/3 i cos α = 2√2/3.

Rozwiązanie:

Dane, sin α = 1/3 i cos α = 2√2/3

Wiemy to, łóżko α = cos α/sin α

⇒ łóżko α = (2√2/3) / (1/3) = 2√2
jaki jest rozmiar mojego monitora

Stąd wartość łóżeczka α = 2√2

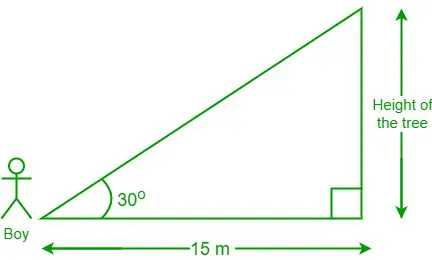
Zadanie 3: Chłopiec stojący 15 m od drzewa patrzy pod kątem 30 stopni do wierzchołka drzewa. Jaka jest wysokość drzewa?

Rozwiązanie:

Wykres z podanych danych
czytanie pliku csv w Javie

Biorąc pod uwagę dane, odległość chłopca od podnóża drzewa = 15 m i θ = 30°

Niech wysokość drzewa będzie wynosić „h”

Mamy, łóżko θ = strona sąsiadująca/strona przeciwna

⇒ łóżko 30° = 15/godz

⇒ √3 = 15/h [ponieważ łóżko 30° = √3]

⇒ godz. = 15/√3

⇒ godz. = 5√3 m

Stąd wysokość drzewa = 5√3 m

Zadanie 4: Znajdź wartość łóżeczka x, jeśli s x = 6/5.

Rozwiązanie:

Dane dane, s x = 6/5

Mamy, sek ² x- tak ² x = 1

⇒ (6/5)²- Więc²x = 1

⇒ 36/25 – tzw²x = 1

⇒ więc²x = 36/25 – 1

⇒ więc²x = 11/25

⇒ tan x = √(11/25) = √11/5

Wiemy to, łóżeczko x = 1/opalenizna x

⇒ łóżko x = 1/(√11/5) = 5/√11

Stąd łóżeczko x = 5/√11

Zadanie 5: Znajdź wartość łóżeczka θ, jeśli cosec θ = 25/24.

Rozwiązanie:

Biorąc pod uwagę dane, cosec θ = 25/24

Wiemy to, łóżko θ = √(cosec ² - 1)

⇒ łóżko θ = √(25/24)²- 1

⇒ łóżko θ =√(625 – 576)/576 = √49/576

⇒ łóżko θ = 7/24

Stąd wartość łóżeczka θ = 7/24

Zadanie 6: Znajdź wartość cot β, jeśli sin β = 5/13.

Rozwiązanie:

Biorąc pod uwagę dane, sin β = 5/13
pandy tworzące ramkę danych

Wiemy to, bez ² β + sałata ² β = 1

⇒ (5/13)²+ bo²β = 1

⇒ kosm²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ sałata β = √144/169 = 12/13

łóżeczko β = cosβ/sin β

= (12/13) / (5/13)

⇒ łóżko β = 12/5

Stąd wartość łóżeczka β = 12/5

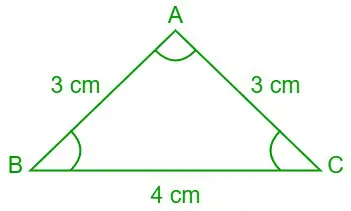
Zadanie 7: Korzystając z prawa cotangensów, znajdź wartości ∠A, ∠B i ∠C (w stopniach), jeśli długości trzech boków trójkąta ABC wynoszą a = 4 cm, b= 3 cm i c= 3 cm.

Rozwiązanie:

Biorąc pod uwagę, a = 4 cm, b = 3 cm i c = 3 cm

Trójkąt ABC

Z prawa kotangencji wynika, że

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Teraz s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – do = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Promień trójkąta r = 2/√5

Z równania prawa kotangentów wynika, że

łóżeczko dziecięce (A/2)/1 = 1/(2/√5)

⇒ łóżeczko (A/2) = √5/2 ⇒ A/2 = łóżeczko^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

łóżeczko dziecięce(B/2)/2 = 1/(2/√5)

⇒ łóżeczko(B/2)/2 = √5/2 ⇒ łóżeczko (B/2) = √5

⇒ (B/2) = łóżko dziecięce^-1(√5) = 24,1° ⇒ ∠B = 48,2°

łóżeczko dziecięce (C/2)/2 = 1/(2/√5)

⇒ łóżeczko(C/2) = √5 ⇒ (C/2) = łóżeczko^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Zatem kąty trójkąta ABC wynoszą ∠A = 83,6°, ∠B = 48,2° i ∠C = 48,2°.