A Lada to urządzenie, które przechowuje (a czasami wyświetla) liczbę wystąpień określonego zdarzenia lub procesu, często w powiązaniu z sygnałem zegarowym. Liczniki są stosowane w elektronice cyfrowej do celów zliczania, mogą zliczać określone zdarzenia zachodzące w obwodzie. Na przykład w liczniku UP licznik zwiększa licznik z każdym narastającym zboczem zegara. Licznik nie tylko liczy, ale może podążać za określoną sekwencją opartą na naszym projekcie, jak każda losowa sekwencja 0,1,3,2… Można je również zaprojektować za pomocą klapek. Wykorzystuje się je jako dzielniki częstotliwości, gdzie dzieli się częstotliwość danego przebiegu impulsowego. Liczniki to układ sekwencyjny, który zlicza liczbę impulsów w postaci kodu binarnego lub BCD. Główne właściwości licznika to synchronizacja, sekwencjonowanie i zliczanie. Licznik działa w dwóch trybach
Licznik w górę
Licznik w dół
Klasyfikacja liczników
Liczniki można ogólnie podzielić na dwie kategorie
- Licznik asynchroniczny
- Licznik synchroniczny
1. Licznik asynchroniczny
W liczniku asynchronicznym nie używamy zegara uniwersalnego, tylko pierwszy przerzutnik jest sterowany przez zegar główny, a wejście zegara pozostałych przerzutników jest sterowane przez wyjście poprzednich przerzutników. Możemy to zrozumieć, postępując zgodnie ze schematem
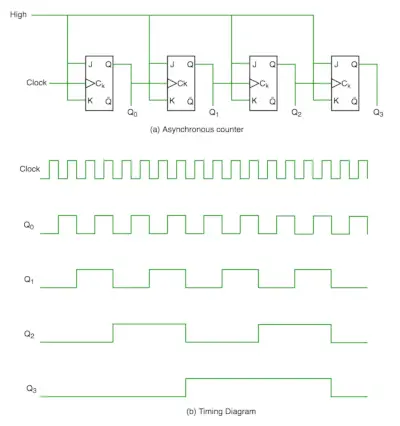
Z wykresu czasowego jasno wynika, że Q0 zmienia się, gdy tylko napotkane zostanie narastające zbocze impulsu zegara, Q1 zmienia się, gdy napotkane zostanie narastające zbocze Q0 (ponieważ Q0 jest jak impuls zegarowy dla drugiego przerzutnika) i tak dalej. W ten sposób generowane są tętnienia poprzez Q0, Q1, Q2, Q3, stąd jest to również nazywane Licznik RIPPLE i licznik szeregowy. Licznik tętnień to kaskadowy układ przerzutników, w którym sygnał wyjściowy jednego przerzutnika steruje wejściem zegara następnego przerzutnika
2. Licznik synchroniczny
W przeciwieństwie do licznika asynchronicznego, licznik synchroniczny ma jeden zegar globalny, który steruje każdym przerzutnikiem, więc dane wyjściowe zmieniają się równolegle. Jedyną zaletą licznika synchronicznego w porównaniu z licznikiem asynchronicznym jest to, że może on działać na wyższej częstotliwości niż licznik asynchroniczny, ponieważ nie ma skumulowanego opóźnienia, ponieważ ten sam zegar jest przydzielany każdemu przerzutnikowi. Nazywa się go również licznikiem równoległym.
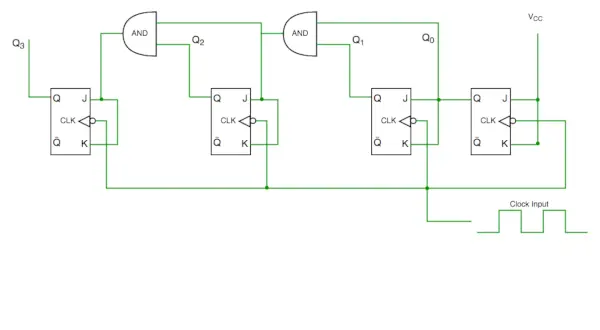
Synchroniczny obwód licznika
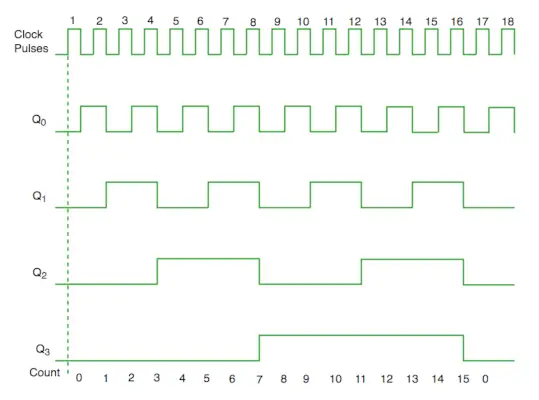
Licznik synchroniczny wykresu czasowego
Ze schematu widzimy, że bit Q0 odpowiada na każde opadające zbocze zegara, podczas gdy Q1 zależy od Q0, Q2 zależy od Q1 i Q0, Q3 zależy od Q2, Q1 i Q0.
Licznik dekad
Licznik dekady zlicza dziesięć różnych stanów, a następnie resetuje się do stanów początkowych. Prosty licznik dekad będzie liczył od 0 do 9, ale możemy również stworzyć liczniki dekad, które mogą przechodzić przez dowolne dziesięć stanów od 0 do 15 (dla licznika 4-bitowego).
| Impuls zegarowy | Pytanie 3 | Pytanie 2 | Pytanie 1 | Pytanie 0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Tabela prawdy dla prostego licznika dekad
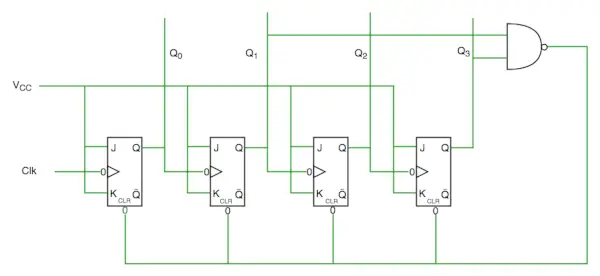
Schemat obwodu licznika dekad
Na schemacie obwodu widzimy, że użyliśmy bramki Nand dla Q3 i Q1 i zasilamy ją w celu wyczyszczenia linii wejściowej, ponieważ binarna reprezentacja liczby 10 to:
1010
I widzimy, że Q3 i Q1 mają tutaj wartość 1. Jeśli podamy NAND tych dwóch bitów w celu wyczyszczenia wejścia, wówczas licznik będzie wyzerowany na poziomie 10 i ponownie zacznie się od początku.
Ważny punkt : Liczba przerzutników używanych w liczniku jest zawsze większa niż równa ( dziennik2N ) gdzie n=liczba stanów w liczniku.
Niektóre pytania dotyczące bramek z poprzednich lat dotyczące liczników
Pytanie 1. Rozważ częściową implementację 2-bitowego licznika przy użyciu przerzutników T zgodnie z sekwencją 0-2-3-1-0, jak pokazano poniżej
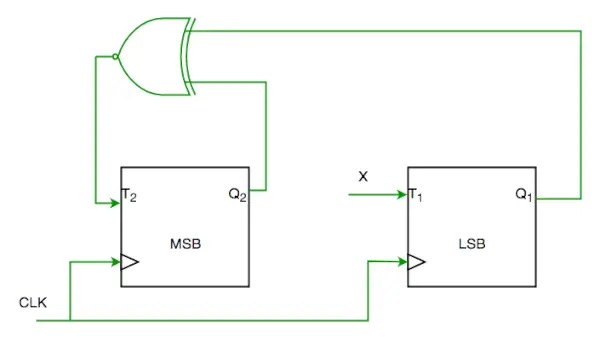
Aby zakończyć obwód, wejście X powinno być
(A) Pytanie 2?
(B) Q2 + Q1
(C) (Q1? Q2)”
(D) Pytanie 1? Pytanie 2 (BRAMA-CS-2004)
Rozwiązanie:
Z obwodu widzimy
T1=XQ1’+X’Q1—-(1)
I
T2=(Q2 ? Q1)’—-(2)
A ŻĄDANE WYJŚCIE TO 00->10->11->01->00
WIĘC X POWINNO BYĆ Q1Q2’+Q1’Q2 SAtysfakcjonujące 1 i 2.
TAK ANS JEST (D) CZĘŚĆ.
Pytanie 2. Poniżej podano funkcje sygnału sterującego 4-bitowego licznika binarnego (gdzie X jest obojętne)
Licznik jest podłączony w następujący sposób:
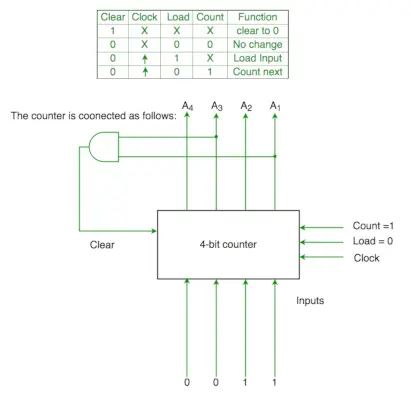
Załóżmy, że opóźnienia licznika i bramki są pomijalne. Jeśli licznik zaczyna się od 0, następuje cykliczna sekwencja:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (BRAMA-CS-2007)
Rozwiązanie:
Początkowo A1 A2 A3 A4 =0000
Clr=A1 i A3
Zatem gdy oba A1 i A3 mają wartość 1, ponownie przechodzi do 0000
Stąd 0000(init.) -> 0001(A1 i A3=0)->0010 (A1 i A3=0) -> 0011(A1 i A3=0) -> 0100 ( A1 i A3=1 )[wyraźny warunek spełniony] ->0000(init.), więc przechodzi przez 0->1->2->3->4
Ans to część (C).
lista vs zestaw w Javie
Quiz na temat logiki cyfrowej
Artykuł napisany przez Anuj Batham,
