W tym artykule omówiono standard szyfrowania danych (DES), historyczny algorytm szyfrowania znany z 56-bitowej długości klucza. Badamy jego działanie, transformację klucza i proces szyfrowania, rzucając światło na jego rolę w bezpieczeństwie danych i jego słabe punkty w dzisiejszym kontekście.
Co to jest DES?
Data Encryption Standard (DES) to szyfr blokowy z 56-bitowym kluczem, który odegrał znaczącą rolę w bezpieczeństwie danych . Stwierdzono, że standard szyfrowania danych (DES) jest podatny na bardzo potężne ataki, dlatego też popularność DES nieznacznie spadła. DES jest szyfrem blokowym i szyfruje dane w blokach o rozmiarze 64 bity każdy, co oznacza, że 64 bity zwykłego tekstu trafiają na dane wejściowe do DES, który generuje 64 bity tekstu zaszyfrowanego. Ten sam algorytm i klucz są używane do szyfrowania i odszyfrowanie , z niewielkimi różnicami. Długość klucza to 56 bitów .
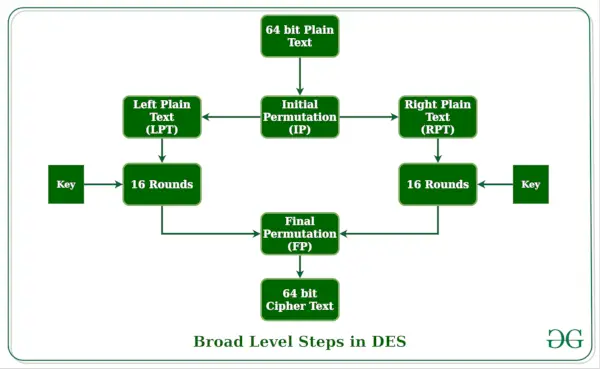
Podstawową ideę pokazano poniżej:
Wspomnieliśmy, że DES używa klucza 56-bitowego. W rzeczywistości klucz początkowy składa się z 64 bitów. Jednak zanim w ogóle rozpocznie się proces DES, co ósmy bit klucza jest odrzucany, tworząc klucz 56-bitowy. Oznacza to, że pozycje bitów 8, 16, 24, 32, 40, 48, 56 i 64 są odrzucane.

Zatem odrzucenie co ósmego bitu klucza daje a Klucz 56-bitowy od oryginału Klucz 64-bitowy .
DES opiera się na dwóch podstawowych atrybutach kryptografia : substytucja (zwana także zamieszaniem) i transpozycja (zwana także dyfuzją). DES składa się z 16 kroków, z których każdy nazywany jest rundą. W każdej rundzie wykonywane są kroki podstawienia i transpozycji. Omówmy teraz kroki ogólne w DES.
- W pierwszym kroku 64-bitowy blok zwykłego tekstu jest przekazywany inicjałowi Permutacja Funkcja (IP).
- Początkowa permutacja jest wykonywana na zwykłym tekście.
- Następnie początkowa permutacja (IP) tworzy dwie połówki permutowanego bloku; mówiąc Zwykły tekst po lewej stronie (LPT) i Zwykły tekst po prawej stronie (RPT).
- Teraz każdy LPT i RPT przechodzi przez 16 rund procesu szyfrowania.
- Na koniec LPT i RPT są ponownie łączone i wykonywana jest końcowa permutacja (FP) na połączonym bloku
- W wyniku tego procesu powstaje 64-bitowy tekst zaszyfrowany.
Początkowa permutacja (IP)
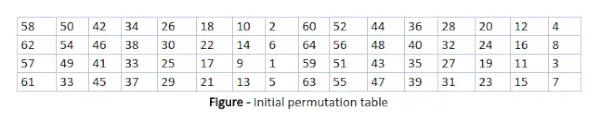
Jak już zauważyliśmy, permutacja początkowa (IP) ma miejsce tylko raz i ma miejsce przed pierwszą rundą. Sugeruje, jak powinna przebiegać transpozycja własności intelektualnej, jak pokazano na rysunku. Na przykład mówi, że adres IP zastępuje pierwszy bit oryginalnego bloku zwykłego tekstu 58. bitem oryginalnego zwykłego tekstu, drugi bit 50. bitem oryginalnego bloku zwykłego tekstu i tak dalej.
To nic innego jak żonglowanie pozycjami bitów oryginalnego bloku tekstu. ta sama zasada dotyczy wszystkich pozostałych pozycji bitów pokazanych na rysunku.
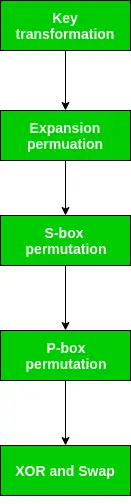
Jak zauważyliśmy, po wykonaniu protokołu IP powstały 64-bitowy permutowany blok tekstu jest dzielony na dwa półbloki. Każdy półblok składa się z 32 bitów, a każda z 16 rund z kolei składa się z kroków ogólnych przedstawionych na rysunku.
Krok 1: Kluczowa transformacja
Zauważyliśmy, że początkowy klucz 64-bitowy jest przekształcany w klucz 56-bitowy poprzez odrzucenie co 8 bitu klucza początkowego. Zatem dla każdego dostępny jest klucz 56-bitowy. Z tego 56-bitowego klucza podczas każdej rundy generowany jest inny 48-bitowy klucz podrzędny w procesie zwanym transformacją klucza. W tym celu 56-bitowy klucz jest podzielony na dwie połowy, każda po 28 bitów. Połówki te są kołowo przesunięte w lewo o jedną lub dwie pozycje, w zależności od rundy.
Na przykład: jeśli w rundzie są liczby 1, 2, 9 lub 16, przesunięcie odbywa się tylko o jedną pozycję, w przypadku pozostałych rund przesunięcie okrężne odbywa się o dwie pozycje. Liczba bitów klucza przesuniętych w rundzie jest pokazana na rysunku.

Po odpowiednim przesunięciu wybieranych jest 48 z 56 bitów. Z 48 możemy uzyskać 64 lub 56 bitów w zależności od wymagań, co pomaga nam rozpoznać, że ten model jest bardzo wszechstronny i może obsłużyć dowolny zakres wymaganych lub spełnionych wymagań. w celu wybrania 48 z 56 bitów tabelę pokazano na rysunku poniżej. Na przykład po przesunięciu bit numer 14 przesuwa się na pierwszą pozycję, bit numer 17 przesuwa się na drugą pozycję i tak dalej. Jeśli przyjrzymy się tabeli, zdamy sobie sprawę, że zawiera ona tylko pozycje 48-bitowe. Bit numer 18 jest odrzucany (nie znajdziemy go w tabeli), podobnie jak 7 innych, aby zredukować klucz 56-bitowy do klucza 48-bitowego. Ponieważ proces transformacji klucza obejmuje permutację, a także wybór 48-bitowego podzbioru oryginalnego 56-bitowego klucza, nazywa się to permutacją kompresji.
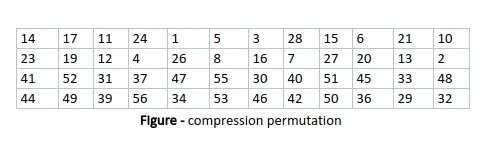
Ze względu na tę technikę permutacji kompresji w każdej rundzie używany jest inny podzbiór bitów klucza. To sprawia, że DES nie jest łatwy do złamania.
Krok 2: Permutacja ekspansji
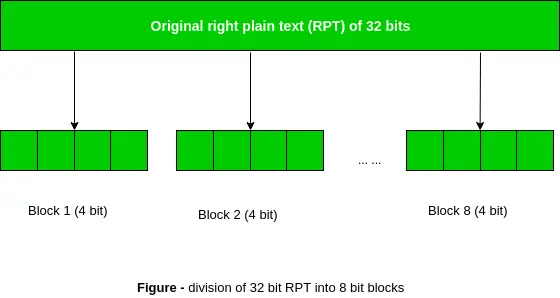
Przypomnijmy, że po początkowej permutacji mieliśmy dwa 32-bitowe obszary zwykłego tekstu, zwane zwykłym tekstem lewym (LPT) i zwykłym tekstem prawym (RPT). Podczas permutacji rozszerzania, RPT jest rozszerzany z 32 bitów do 48 bitów. Bity są również permutowane, stąd nazywa się to permutacją rozszerzającą. Dzieje się tak, gdy 32-bitowy RPT jest podzielony na 8 bloków, z których każdy składa się z 4 bitów. Następnie każdy 4-bitowy blok z poprzedniego kroku jest następnie rozszerzany do odpowiedniego bloku 6-bitowego, tj. na każdy 4-bitowy blok dodawane są 2 dodatkowe bity.
Proces ten powoduje rozwinięcie, a także permutację bitu wejściowego podczas tworzenia sygnału wyjściowego. Proces transformacji klucza kompresuje klucz 56-bitowy do 48 bitów. Następnie proces permutacji rozszerzania rozszerza 32-bitowy RPT Do 48-bitowy . Teraz klucz 48-bitowy jest BEZPŁATNY z 48-bitowym RPT, a wynikowy wynik jest przekazywany do następnego kroku, czyli Podstawienie S-Box .
Pyton
długość łańcucha w Javie
# Python3 code for the above approach> # Hexadecimal to binary conversion> def> hex2bin(s):> >mp>=> {>'0'>:>'0000'>,> >'1'>:>'0001'>,> >'2'>:>'0010'>,> >'3'>:>'0011'>,> >'4'>:>'0100'>,> >'5'>:>'0101'>,> >'6'>:>'0110'>,> >'7'>:>'0111'>,> >'8'>:>'1000'>,> >'9'>:>'1001'>,> >'A'>:>'1010'>,> >'B'>:>'1011'>,> >'C'>:>'1100'>,> >'D'>:>'1101'>,> >'E'>:>'1110'>,> >'F'>:>'1111'>}> >bin> => ''> >for> i>in> range>(>len>(s)):> >bin> => bin> +> mp[s[i]]> >return> bin> # Binary to hexadecimal conversion> def> bin2hex(s):> >mp>=> {>'0000'>:>'0'>,> >'0001'>:>'1'>,> >'0010'>:>'2'>,> >'0011'>:>'3'>,> >'0100'>:>'4'>,> >'0101'>:>'5'>,> >'0110'>:>'6'>,> >'0111'>:>'7'>,> >'1000'>:>'8'>,> >'1001'>:>'9'>,> >'1010'>:>'A'>,> >'1011'>:>'B'>,> >'1100'>:>'C'>,> >'1101'>:>'D'>,> >'1110'>:>'E'>,> >'1111'>:>'F'>}> >hex> => ''> >for> i>in> range>(>0>,>len>(s),>4>):> >ch>=> ''> >ch>=> ch>+> s[i]> >ch>=> ch>+> s[i>+> 1>]> >ch>=> ch>+> s[i>+> 2>]> >ch>=> ch>+> s[i>+> 3>]> >hex> => hex> +> mp[ch]> >return> hex> # Binary to decimal conversion> def> bin2dec(binary):> >binary1>=> binary> >decimal, i, n>=> 0>,>0>,>0> >while>(binary !>=> 0>):> >dec>=> binary>%> 10> >decimal>=> decimal>+> dec>*> pow>(>2>, i)> >binary>=> binary>/>/>10> >i>+>=> 1> >return> decimal> # Decimal to binary conversion> def> dec2bin(num):> >res>=> bin>(num).replace(>'0b'>, '')> >if>(>len>(res)>%> 4> !>=> 0>):> >div>=> len>(res)>/> 4> >div>=> int>(div)> >counter>=> (>4> *> (div>+> 1>))>-> len>(res)> >for> i>in> range>(>0>, counter):> >res>=> '0'> +> res> >return> res> # Permute function to rearrange the bits> def> permute(k, arr, n):> >permutation>=> ''> >for> i>in> range>(>0>, n):> >permutation>=> permutation>+> k[arr[i]>-> 1>]> >return> permutation> # shifting the bits towards left by nth shifts> def> shift_left(k, nth_shifts):> >s>=> ''> >for> i>in> range>(nth_shifts):> >for> j>in> range>(>1>,>len>(k)):> >s>=> s>+> k[j]> >s>=> s>+> k[>0>]> >k>=> s> >s>=> ''> >return> k> # calculating xow of two strings of binary number a and b> def> xor(a, b):> >ans>=> ''> >for> i>in> range>(>len>(a)):> >if> a[i]>=>=> b[i]:> >ans>=> ans>+> '0'> >else>:> >ans>=> ans>+> '1'> >return> ans> # Table of Position of 64 bits at initial level: Initial Permutation Table> initial_perm>=> [>58>,>50>,>42>,>34>,>26>,>18>,>10>,>2>,> >60>,>52>,>44>,>36>,>28>,>20>,>12>,>4>,> >62>,>54>,>46>,>38>,>30>,>22>,>14>,>6>,> >64>,>56>,>48>,>40>,>32>,>24>,>16>,>8>,> >57>,>49>,>41>,>33>,>25>,>17>,>9>,>1>,> >59>,>51>,>43>,>35>,>27>,>19>,>11>,>3>,> >61>,>53>,>45>,>37>,>29>,>21>,>13>,>5>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,>7>]> # Expansion D-box Table> exp_d>=> [>32>,>1>,>2>,>3>,>4>,>5>,>4>,>5>,> >6>,>7>,>8>,>9>,>8>,>9>,>10>,>11>,> >12>,>13>,>12>,>13>,>14>,>15>,>16>,>17>,> >16>,>17>,>18>,>19>,>20>,>21>,>20>,>21>,> >22>,>23>,>24>,>25>,>24>,>25>,>26>,>27>,> >28>,>29>,>28>,>29>,>30>,>31>,>32>,>1>]> # Straight Permutation Table> per>=> [>16>,>7>,>20>,>21>,> >29>,>12>,>28>,>17>,> >1>,>15>,>23>,>26>,> >5>,>18>,>31>,>10>,> >2>,>8>,>24>,>14>,> >32>,>27>,>3>,>9>,> >19>,>13>,>30>,>6>,> >22>,>11>,>4>,>25>]> # S-box Table> sbox>=> [[[>14>,>4>,>13>,>1>,>2>,>15>,>11>,>8>,>3>,>10>,>6>,>12>,>5>,>9>,>0>,>7>],> >[>0>,>15>,>7>,>4>,>14>,>2>,>13>,>1>,>10>,>6>,>12>,>11>,>9>,>5>,>3>,>8>],> >[>4>,>1>,>14>,>8>,>13>,>6>,>2>,>11>,>15>,>12>,>9>,>7>,>3>,>10>,>5>,>0>],> >[>15>,>12>,>8>,>2>,>4>,>9>,>1>,>7>,>5>,>11>,>3>,>14>,>10>,>0>,>6>,>13>]],> >[[>15>,>1>,>8>,>14>,>6>,>11>,>3>,>4>,>9>,>7>,>2>,>13>,>12>,>0>,>5>,>10>],> >[>3>,>13>,>4>,>7>,>15>,>2>,>8>,>14>,>12>,>0>,>1>,>10>,>6>,>9>,>11>,>5>],> >[>0>,>14>,>7>,>11>,>10>,>4>,>13>,>1>,>5>,>8>,>12>,>6>,>9>,>3>,>2>,>15>],> >[>13>,>8>,>10>,>1>,>3>,>15>,>4>,>2>,>11>,>6>,>7>,>12>,>0>,>5>,>14>,>9>]],> >[[>10>,>0>,>9>,>14>,>6>,>3>,>15>,>5>,>1>,>13>,>12>,>7>,>11>,>4>,>2>,>8>],> >[>13>,>7>,>0>,>9>,>3>,>4>,>6>,>10>,>2>,>8>,>5>,>14>,>12>,>11>,>15>,>1>],> >[>13>,>6>,>4>,>9>,>8>,>15>,>3>,>0>,>11>,>1>,>2>,>12>,>5>,>10>,>14>,>7>],> >[>1>,>10>,>13>,>0>,>6>,>9>,>8>,>7>,>4>,>15>,>14>,>3>,>11>,>5>,>2>,>12>]],> >[[>7>,>13>,>14>,>3>,>0>,>6>,>9>,>10>,>1>,>2>,>8>,>5>,>11>,>12>,>4>,>15>],> >[>13>,>8>,>11>,>5>,>6>,>15>,>0>,>3>,>4>,>7>,>2>,>12>,>1>,>10>,>14>,>9>],> >[>10>,>6>,>9>,>0>,>12>,>11>,>7>,>13>,>15>,>1>,>3>,>14>,>5>,>2>,>8>,>4>],> >[>3>,>15>,>0>,>6>,>10>,>1>,>13>,>8>,>9>,>4>,>5>,>11>,>12>,>7>,>2>,>14>]],> >[[>2>,>12>,>4>,>1>,>7>,>10>,>11>,>6>,>8>,>5>,>3>,>15>,>13>,>0>,>14>,>9>],> >[>14>,>11>,>2>,>12>,>4>,>7>,>13>,>1>,>5>,>0>,>15>,>10>,>3>,>9>,>8>,>6>],> >[>4>,>2>,>1>,>11>,>10>,>13>,>7>,>8>,>15>,>9>,>12>,>5>,>6>,>3>,>0>,>14>],> >[>11>,>8>,>12>,>7>,>1>,>14>,>2>,>13>,>6>,>15>,>0>,>9>,>10>,>4>,>5>,>3>]],> >[[>12>,>1>,>10>,>15>,>9>,>2>,>6>,>8>,>0>,>13>,>3>,>4>,>14>,>7>,>5>,>11>],> >[>10>,>15>,>4>,>2>,>7>,>12>,>9>,>5>,>6>,>1>,>13>,>14>,>0>,>11>,>3>,>8>],> >[>9>,>14>,>15>,>5>,>2>,>8>,>12>,>3>,>7>,>0>,>4>,>10>,>1>,>13>,>11>,>6>],> >[>4>,>3>,>2>,>12>,>9>,>5>,>15>,>10>,>11>,>14>,>1>,>7>,>6>,>0>,>8>,>13>]],> >[[>4>,>11>,>2>,>14>,>15>,>0>,>8>,>13>,>3>,>12>,>9>,>7>,>5>,>10>,>6>,>1>],> >[>13>,>0>,>11>,>7>,>4>,>9>,>1>,>10>,>14>,>3>,>5>,>12>,>2>,>15>,>8>,>6>],> >[>1>,>4>,>11>,>13>,>12>,>3>,>7>,>14>,>10>,>15>,>6>,>8>,>0>,>5>,>9>,>2>],> >[>6>,>11>,>13>,>8>,>1>,>4>,>10>,>7>,>9>,>5>,>0>,>15>,>14>,>2>,>3>,>12>]],> >[[>13>,>2>,>8>,>4>,>6>,>15>,>11>,>1>,>10>,>9>,>3>,>14>,>5>,>0>,>12>,>7>],> >[>1>,>15>,>13>,>8>,>10>,>3>,>7>,>4>,>12>,>5>,>6>,>11>,>0>,>14>,>9>,>2>],> >[>7>,>11>,>4>,>1>,>9>,>12>,>14>,>2>,>0>,>6>,>10>,>13>,>15>,>3>,>5>,>8>],> >[>2>,>1>,>14>,>7>,>4>,>10>,>8>,>13>,>15>,>12>,>9>,>0>,>3>,>5>,>6>,>11>]]]> # Final Permutation Table> final_perm>=> [>40>,>8>,>48>,>16>,>56>,>24>,>64>,>32>,> >39>,>7>,>47>,>15>,>55>,>23>,>63>,>31>,> >38>,>6>,>46>,>14>,>54>,>22>,>62>,>30>,> >37>,>5>,>45>,>13>,>53>,>21>,>61>,>29>,> >36>,>4>,>44>,>12>,>52>,>20>,>60>,>28>,> >35>,>3>,>43>,>11>,>51>,>19>,>59>,>27>,> >34>,>2>,>42>,>10>,>50>,>18>,>58>,>26>,> >33>,>1>,>41>,>9>,>49>,>17>,>57>,>25>]> def> encrypt(pt, rkb, rk):> >pt>=> hex2bin(pt)> ># Initial Permutation> >pt>=> permute(pt, initial_perm,>64>)> >print>(>'After initial permutation'>, bin2hex(pt))> ># Splitting> >left>=> pt[>0>:>32>]> >right>=> pt[>32>:>64>]> >for> i>in> range>(>0>,>16>):> ># Expansion D-box: Expanding the 32 bits data into 48 bits> >right_expanded>=> permute(right, exp_d,>48>)> ># XOR RoundKey[i] and right_expanded> >xor_x>=> xor(right_expanded, rkb[i])> ># S-boxex: substituting the value from s-box table by calculating row and column> >sbox_str>=> ''> >for> j>in> range>(>0>,>8>):> >row>=> bin2dec(>int>(xor_x[j>*> 6>]>+> xor_x[j>*> 6> +> 5>]))> >col>=> bin2dec(> >int>(xor_x[j>*> 6> +> 1>]>+> xor_x[j>*> 6> +> 2>]>+> xor_x[j>*> 6> +> 3>]>+> xor_x[j>*> 6> +> 4>]))> >val>=> sbox[j][row][col]> >sbox_str>=> sbox_str>+> dec2bin(val)> ># Straight D-box: After substituting rearranging the bits> >sbox_str>=> permute(sbox_str, per,>32>)> ># XOR left and sbox_str> >result>=> xor(left, sbox_str)> >left>=> result> ># Swapper> >if>(i !>=> 15>):> >left, right>=> right, left> >print>(>'Round '>, i>+> 1>,>' '>, bin2hex(left),> >' '>, bin2hex(right),>' '>, rk[i])> ># Combination> >combine>=> left>+> right> ># Final permutation: final rearranging of bits to get cipher text> >cipher_text>=> permute(combine, final_perm,>64>)> >return> cipher_text> pt>=> '123456ABCD132536'> key>=> 'AABB09182736CCDD'> # Key generation> # --hex to binary> key>=> hex2bin(key)> # --parity bit drop table> keyp>=> [>57>,>49>,>41>,>33>,>25>,>17>,>9>,> >1>,>58>,>50>,>42>,>34>,>26>,>18>,> >10>,>2>,>59>,>51>,>43>,>35>,>27>,> >19>,>11>,>3>,>60>,>52>,>44>,>36>,> >63>,>55>,>47>,>39>,>31>,>23>,>15>,> >7>,>62>,>54>,>46>,>38>,>30>,>22>,> >14>,>6>,>61>,>53>,>45>,>37>,>29>,> >21>,>13>,>5>,>28>,>20>,>12>,>4>]> # getting 56 bit key from 64 bit using the parity bits> key>=> permute(key, keyp,>56>)> # Number of bit shifts> shift_table>=> [>1>,>1>,>2>,>2>,> >2>,>2>,>2>,>2>,> >1>,>2>,>2>,>2>,> >2>,>2>,>2>,>1>]> # Key- Compression Table : Compression of key from 56 bits to 48 bits> key_comp>=> [>14>,>17>,>11>,>24>,>1>,>5>,> >3>,>28>,>15>,>6>,>21>,>10>,> >23>,>19>,>12>,>4>,>26>,>8>,> >16>,>7>,>27>,>20>,>13>,>2>,> >41>,>52>,>31>,>37>,>47>,>55>,> >30>,>40>,>51>,>45>,>33>,>48>,> >44>,>49>,>39>,>56>,>34>,>53>,> >46>,>42>,>50>,>36>,>29>,>32>]> # Splitting> left>=> key[>0>:>28>]># rkb for RoundKeys in binary> right>=> key[>28>:>56>]># rk for RoundKeys in hexadecimal> rkb>=> []> rk>=> []> for> i>in> range>(>0>,>16>):> ># Shifting the bits by nth shifts by checking from shift table> >left>=> shift_left(left, shift_table[i])> >right>=> shift_left(right, shift_table[i])> ># Combination of left and right string> >combine_str>=> left>+> right> ># Compression of key from 56 to 48 bits> >round_key>=> permute(combine_str, key_comp,>48>)> >rkb.append(round_key)> >rk.append(bin2hex(round_key))> print>(>'Encryption'>)> cipher_text>=> bin2hex(encrypt(pt, rkb, rk))> print>(>'Cipher Text : '>, cipher_text)> print>(>'Decryption'>)> rkb_rev>=> rkb[::>->1>]> rk_rev>=> rk[::>->1>]> text>=> bin2hex(encrypt(cipher_text, rkb_rev, rk_rev))> print>(>'Plain Text : '>, text)> # This code is contributed by Aditya Jain> |
>
>
JavaScript
poradnik Java dla początkujących
// Define DES key and plaintext> const key =>'0123456789abcdef'>;> const plaintext =>'Hello, world!'>;> // Perform DES encryption> const des =>new> DES(key);> const ciphertext = des.encrypt(plaintext);> // Perform DES decryption> const decrypted = des.decrypt(ciphertext);> // Print results> console.log(>'Plaintext: '>, plaintext);> console.log(>'Ciphertext: '>, ciphertext);> console.log(>'Decrypted: '>, decrypted);> // Define DES class> class DES {> >constructor(key) {> >// Initialize DES with key> >this>.key = CryptoJS.enc.Hex.parse(key);> >}> >encrypt(plaintext) {> >// Perform DES encryption on plaintext> >const encrypted = CryptoJS.DES.encrypt(> >plaintext,> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return ciphertext as hex string> >return> encrypted.ciphertext.toString();> >}> >decrypt(ciphertext) {> >// Parse ciphertext from hex string> >const ciphertextHex = CryptoJS.enc.Hex.parse(ciphertext);> >// Perform DES decryption on ciphertext> >const decrypted = CryptoJS.DES.decrypt(> >{ ciphertext: ciphertextHex },> >this>.key,> >{ mode: CryptoJS.mode.ECB }> >);> >// Return decrypted plaintext as UTF-8 string> >return> decrypted.toString(CryptoJS.enc.Utf8);> >}> }> |
>
>Wyjście
...60AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Wyjście:
Encryption: After initial permutation: 14A7D67818CA18AD After splitting: L0=14A7D678 R0=18CA18AD Round 1 18CA18AD 5A78E394 194CD072DE8C Round 2 5A78E394 4A1210F6 4568581ABCCE Round 3 4A1210F6 B8089591 06EDA4ACF5B5 Round 4 B8089591 236779C2 DA2D032B6EE3 Round 5 236779C2 A15A4B87 69A629FEC913 Round 6 A15A4B87 2E8F9C65 C1948E87475E Round 7 2E8F9C65 A9FC20A3 708AD2DDB3C0 Round 8 A9FC20A3 308BEE97 34F822F0C66D Round 9 308BEE97 10AF9D37 84BB4473DCCC Round 10 10AF9D37 6CA6CB20 02765708B5BF Round 11 6CA6CB20 FF3C485F 6D5560AF7CA5 Round 12 FF3C485F 22A5963B C2C1E96A4BF3 Round 13 22A5963B 387CCDAA 99C31397C91F Round 14 387CCDAA BD2DD2AB 251B8BC717D0 Round 15 BD2DD2AB CF26B472 3330C5D9A36D Round 16 19BA9212 CF26B472 181C5D75C66D Cipher Text: C0B7A8D05F3A829C Decryption After initial permutation: 19BA9212CF26B472 After splitting: L0=19BA9212 R0=CF26B472 Round 1 CF26B472 BD2DD2AB 181C5D75C66D Round 2 BD2DD2AB 387CCDAA 3330C5D9A36D Round 3 387CCDAA 22A5963B 251B8BC717D0 Round 4 22A5963B FF3C485F 99C31397C91F Round 5 FF3C485F 6CA6CB20 C2C1E96A4BF3 Round 6 6CA6CB20 10AF9D37 6D5560AF7CA5 Round 7 10AF9D37 308BEE97 02765708B5BF Round 8 308BEE97 A9FC20A3 84BB4473DCCC Round 9 A9FC20A3 2E8F9C65 34F822F0C66D Round 10 2E8F9C65 A15A4B87 708AD2DDB3C0 Round 11 A15A4B87 236779C2 C1948E87475E Round 12 236779C2 B8089591 69A629FEC913 Round 13 B8089591 4A1210F6 DA2D032B6EE3 Round 14 4A1210F6 5A78E394 06EDA4ACF5B5 Round 15 5A78E394 18CA18AD 4568581ABCCE Round 16 14A7D678 18CA18AD 194CD072DE8C Plain Text: 123456ABCD132536>
Wniosek
Podsumowując, standard szyfrowania danych (DES) to: szyfr blokowy z kluczem o długości 56 bitów, który odegrał znaczącą rolę w bezpieczeństwie danych. Jednak z powodu luk w zabezpieczeniach jego popularność spadła. DES działa poprzez serię rund obejmujących transformację klucza, permutację rozwinięcia i podstawienie, ostatecznie tworząc tekst zaszyfrowany z tekstu jawnego. Chociaż DES ma znaczenie historyczne, należy rozważyć rozwiązanie bezpieczniejsze szyfrowanie alternatywy dla współczesnych potrzeb ochrony danych.
Często Zadawane Pytania
Pytanie 1 : Co należy rozważyć jako alternatywę dla DES w zakresie szyfrowania danych?
Odpowiedź:
W przypadku współczesnych potrzeb szyfrowania danych rozważ użycie silniejszych algorytmów szyfrowania, takich jak AES (Zaawansowany Standard Szyfrowania).
Pytanie 2 : W jaki sposób generowany jest 48-bitowy podklucz dla każdej rundy w DES?
Odpowiedź:
48-bitowy podklucz dla każdej rundy w DES jest wyprowadzany z 56-bitowego klucza w procesie cyklicznego przesuwania i permutacji, zapewniając różnorodność kluczy.

