Algorytm euklidesowy to sposób na znalezienie największego wspólnego dzielnika dwóch dodatnich liczb całkowitych. NWD dwóch liczb to największa liczba dzieląca obie liczby. Prostym sposobem na znalezienie NWD jest rozłożenie obu liczb na czynniki i pomnożenie wspólnych czynników pierwszych.
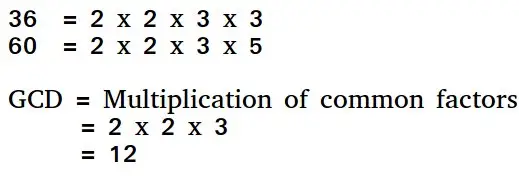
Podstawowy algorytm euklidesowy dla GCD:
Algorytm opiera się na poniższych faktach.
- Jeśli odejmiemy mniejszą liczbę od większej (zmniejszymy większą liczbę), GCD się nie zmieni. Jeśli więc będziemy odejmować wielokrotnie większą z dwóch, otrzymamy NWD.
- Teraz zamiast odejmowania, jeśli podzielimy mniejszą liczbę, algorytm zatrzymuje się, gdy znajdziemy resztę 0.
Poniżej znajduje się funkcja rekurencyjna do oceny gcd przy użyciu algorytmu Euclida:
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 35, b = 10;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 31, b = 2;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >return> 0;> }> |
>
>
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 35, b = 10;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 31, b = 2;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >return> 0;> }> |
>
bfs i dfs
>
Jawa
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a ==>0>)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver code> >public> static> void> main(String[] args)> >{> >int> a =>10>, b =>15>, g;> > >// Function call> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>35>;> >b =>10>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>31>;> >b =>2>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // Code Contributed by Mohit Gupta_OMG> |
>
>
Python3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> >if> a>=>=> 0>:> >return> b> >return> gcd(b>%> a, a)> # Driver code> if> __name__>=>=> '__main__'>:> >a>=> 10> >b>=> 15> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 35> >b>=> 10> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 31> >b>=> 2> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
>
>
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver Code> >static> public> void> Main()> >{> >int> a = 10, b = 15, g;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 35;> >b = 10;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 31;> >b = 2;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // This code is contributed by ajit> |
>
>
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>> |
>
>
JavaScript
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> >let a = 10, b = 15;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 35, b = 10;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 31, b = 2;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> // This code contributed by aashish1995> |
>
>
pasmo podstawowe vs łącze szerokopasmoweWyjście
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1>
Złożoność czasowa: O(log min(a, b))
Przestrzeń pomocnicza: O(log (min(a,b))
Rozszerzony algorytm euklidesowy:
Rozszerzony algorytm euklidesowy znajduje również współczynniki całkowite x i y takie, że: ax + by = gcd(a, b)
Przykłady:
Wejście: a = 30, b = 20
Wyjście: gcd = 10, x = 1, y = -1
(Zauważ, że 30*1 + 20*(-1) = 10)Wejście: a = 35, b = 15
Wyjście: gcd = 5, x = 1, y = -2
(Zauważ, że 35*1 + 15*(-2) = 5)
Rozszerzony algorytm euklidesowy aktualizuje wyniki gcd(a, b) przy użyciu wyników obliczonych przez rekurencyjne wywołanie gcd(b%a, a). Niech wartości x i y obliczone przez wywołanie rekurencyjne będą wynosić x1i y1. x i y są aktualizowane przy użyciu poniższych wyrażeń.
Zalecana praktyka Rozszerzony algorytm euklidesowy Wypróbuj!topór + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x1+ jest1
topór + by = (b%a)x1+ jest1
topór + by = (b – [b/a] * a)x1+ jest1
topór + by = a(y1– [b/a] * x1) + bx1Porównując lewą i prawą stronę,
x = y1– ?b/a? * X1
y = x1
Poniżej implementacja powyższego podejścia:
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of> >// recursive call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Code> int> main()> {> >int> x, y, a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >cout <<>'GCD('> << a <<>', '> << b> ><<>') = '> << g << endl;> >return> 0;> }> |
>
>
C
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of recursive> >// call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Program> int> main()> {> >int> x, y;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >printf>(>'gcd(%d, %d) = %d'>, a, b, g);> >return> 0;> }> |
>
>
Jawa
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,>int> x,> >int> y)> >{> >// Base Case> >if> (a ==>0>) {> >x =>0>;> >y =>1>;> >return> b;> >}> >int> x1 =>1>,> >y1 =>1>;>// To store results of recursive call> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using results of recursive> >// call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> >// Driver Program> >public> static> void> main(String[] args)> >{> >int> x =>1>, y =>1>;> >int> a =>35>, b =>15>;> >int> g = gcdExtended(a, b, x, y);> >System.out.print(>'gcd('> + a +>' , '> + b> >+>') = '> + g);> >}> }> |
>
>
Python3
różnica między lisem a wilkiem
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> ># Base Case> >if> a>=>=> 0>:> >return> b,>0>,>1> >gcd, x1, y1>=> gcdExtended(b>%> a, a)> ># Update x and y using results of recursive> ># call> >x>=> y1>-> (b>/>/>a)>*> x1> >y>=> x1> >return> gcd, x, y> # Driver code> a, b>=> 35>,>15> g, x, y>=> gcdExtended(a, b)> print>(>'gcd('>, a,>','>, b,>') = '>, g)> |
>
>
C#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,> >int> x,>int> y)> >{> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results of> >// recursive call> >int> x1 = 1, y1 = 1;> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using> >// results of recursive call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> > >// Driver Code> >static> public> void> Main ()> >{> >int> x = 1, y = 1;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, x, y);> >Console.WriteLine(>'gcd('> + a +>' , '> +> >b +>') = '> + g);> >}> }> |
>
>
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>> |
>
>
JavaScript
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> >x, y)> {> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results> >// of recursive call> >let gcd = gcdExtended(b % a,> >a, x, y);> >// Update x and y using> >// results of recursive> >// call> >x = y - (b / a) * x;> >y = x;> >return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(>'gcd('> + a);> document.write(>', '> + b +>')'>);> document.write(>' = '> + g);> > |
>
>
Wyjście :
gcd(35, 15) = 5>
Złożoność czasowa: O(log N)
Przestrzeń pomocnicza: O(log N)
Jak działa rozszerzony algorytm?
Jak widać powyżej, x i y są wynikami dla wejść a i b,
a.x + b.y = gcd —-(1)
I x1i y1są wynikami dla wejść b%a i a
(b%a).x1+ ej1= gcd
Kiedy wstawimy b%a = (b – (?b/a?).a) powyżej,
otrzymujemy śledzenie. Zauważ, że ?b/a? to piętro (b/a)(b – (?b/a?).a).x1+ ej1= gcd
Powyższe równanie można również zapisać jak poniżej
b.x1+ a. (i1– (?b/a?).x1) = gcd —(2)
Po porównaniu współczynników „a” i „b” w (1) i
(2), otrzymujemy następujące,
x = y1– ?b/a? * X1
y = x1
W jaki sposób rozszerzony algorytm jest przydatny?
Rozszerzony algorytm Euklidesa jest szczególnie przydatny, gdy aib są względnie pierwsze (lub gcd wynosi 1). Ponieważ x jest modułową multiplikatywną odwrotnością a modulo b, a y jest modułową multiplikatywną odwrotnością b modulo a. W szczególności obliczenie modułowej odwrotności multiplikatywnej jest istotnym krokiem w metodzie szyfrowania kluczem publicznym RSA.
