logo

TechCodeview

Algorytm Floyda Warshalla

The Algorytm Floyda-Warshalla , nazwany na cześć jego twórców Roberta Floyda i Stephena Warshalla , jest podstawowym algorytmem w informatyce i teorii grafów. Służy do znajdowania najkrótszych ścieżek pomiędzy wszystkimi parami węzłów na grafie ważonym. Algorytm ten jest bardzo wydajny i może obsługiwać wykresy w obu przypadkach pozytywny oraz n ujemne wagi krawędzi , co czyni go wszechstronnym narzędziem do rozwiązywania szerokiego zakresu problemów z siecią i łącznością.

Spis treści



Baner algorytmu Floyda-Warshalla

Algorytm Floyda Warshalla:

The Algorytm Floyda Warshalla w odróżnieniu od algorytmu najkrótszej ścieżki obejmującej wszystkie pary Dijkstra I Bellmana Forda które są algorytmami najkrótszej ścieżki z jednego źródła. Algorytm ten działa zarówno dla skierowany I nieukierunkowane ważone wykresy. Nie działa to jednak w przypadku grafów z cyklami ujemnymi (gdzie suma krawędzi w cyklu jest ujemna). Wynika Programowanie dynamiczne podejście polegające na sprawdzeniu każdej możliwej ścieżki przechodzącej przez każdy możliwy węzeł w celu obliczenia najkrótszej odległości między każdą parą węzłów.

Konwersja ciągu znaków na int w Javie

Pomysł na algorytm Floyda Warshall’a:

Załóżmy, że mamy wykres G[][] z W wierzchołki z 1 Do N . Teraz musimy ocenić a najkrótszaPathMatrix[][] gdzie s hortestPathMatrix[i] [j] reprezentuje najkrótszą ścieżkę między wierzchołkami I I J .



Oczywiście najkrótsza droga pomiędzy I Do J będzie trochę k liczba węzłów pośrednich. Ideą algorytmu Floyda Warshalla jest traktowanie każdego wierzchołka 1 Do N jako węzeł pośredni jeden po drugim.

Poniższy rysunek przedstawia powyższą optymalną właściwość podstruktury w algorytmie Floyda Warshalla:

Algorytm algorytmu Floyda Warshalla:

  • W pierwszym kroku zainicjuj macierz rozwiązań taką samą jak macierz wykresu wejściowego.
  • Następnie zaktualizuj macierz rozwiązań, traktując wszystkie wierzchołki jako wierzchołek pośredni.
  • Pomysł polega na tym, aby wybierać wszystkie wierzchołki jeden po drugim i aktualizować wszystkie najkrótsze ścieżki, które obejmują wybrany wierzchołek jako wierzchołek pośredni na najkrótszej ścieżce.
  • Kiedy wybieramy numer wierzchołka k jako wierzchołek pośredni, rozważaliśmy już wierzchołki {0, 1, 2, .. k-1} jako wierzchołki pośrednie.
  • Dla każdej pary (i, j) odpowiednio wierzchołków źródłowego i docelowego, istnieją dwa możliwe przypadki.
    • k nie jest wierzchołkiem pośrednim na najkrótszej ścieżce od I Do J . Zachowujemy wartość odległość[i]j] tak jak jest.
    • k jest wierzchołkiem pośrednim na najkrótszej ścieżce od I Do J . Aktualizujemy wartość odległość[i]j] Jak odległość [i] [k] + odległość [k], Jeśli dist[i][j]> dist[i][k] + dist[k][j]

Pseudokod algorytmu Floyda Warshall'a:>

Dla k = 0 do n – 1
Dla i = 0 do n – 1
Dla j = 0 do n – 1
Odległość[i, j] = min(Odległość[i, j], Odległość[i, k] + Odległość[k, j])



gdzie i = węzeł źródłowy, j = węzeł docelowy, k = węzeł pośredni

Ilustracja algorytmu Floyda Warshalla:

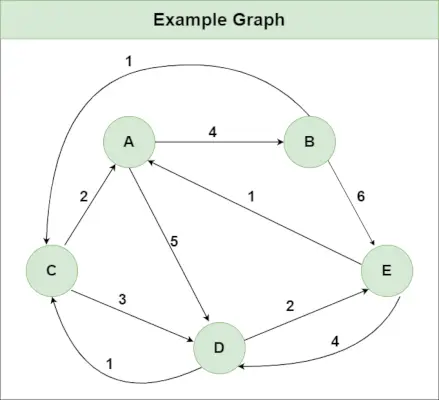
Załóżmy, że mamy wykres pokazany na obrazku:

string.compareto C#
dryRun1drawio

Krok 1 : Zainicjuj macierz odległości[][], korzystając z wykresu wejściowego, tak aby odległość[i][j]= waga krawędzi od I Do J , także Odległość[i] [j] = Nieskończoność, jeśli nie ma krawędzi I Do J.

krok 1rysunek

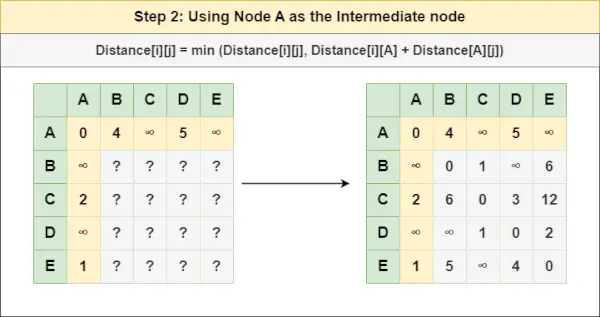
Krok 2 : Leczyć węzeł A jako węzeł pośredni i oblicz Odległość[][] dla każdej pary węzłów {i,j}, korzystając ze wzoru:

= Odległość[i][j] = minimalna (Odległość[i][j], (Odległość od i do A ) + (Odległość od A do j))
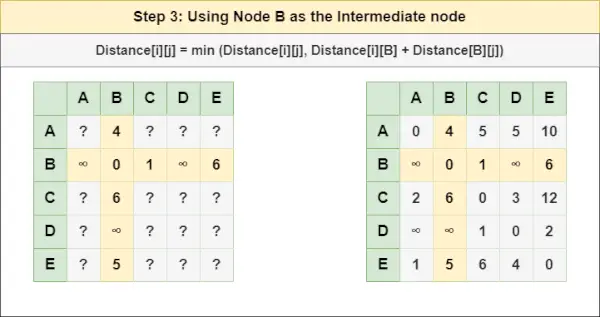
= Odległość[i][j] = minimalna (Odległość[i][j], Odległość[i][ A ] + Odległość [ A ][J])

krok2rysunek

Krok 3 : Leczyć węzeł B jako węzeł pośredni i oblicz Odległość[][] dla każdej pary węzłów {i,j}, korzystając ze wzoru:

= Odległość[i][j] = minimalna (Odległość[i][j], (Odległość od i do B ) + (Odległość od B do j))
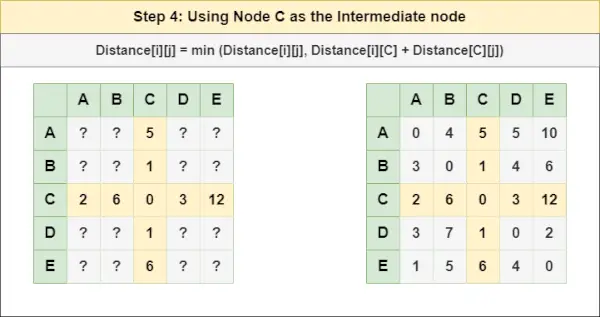
= Odległość[i][j] = minimalna (Odległość[i][j], Odległość[i][ B ] + Odległość [ B ][J])

krok 3rysunek

Krok 4 : Leczyć węzeł C jako węzeł pośredni i oblicz Odległość[][] dla każdej pary węzłów {i,j}, korzystając ze wzoru:

= Odległość[i][j] = minimalna (Odległość[i][j], (Odległość od i do C ) + (Odległość od C do j))
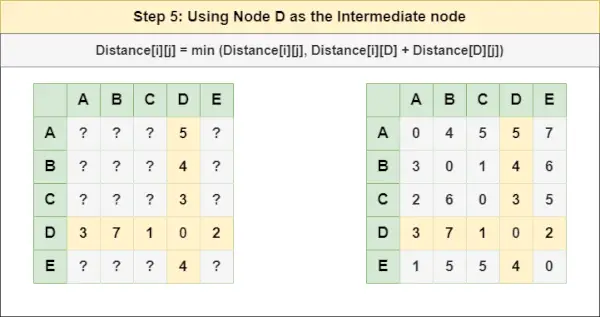
= Odległość[i][j] = minimalna (Odległość[i][j], Odległość[i][ C ] + Odległość [ C ][J])

step4drawio

Krok 5 : Leczyć węzeł D jako węzeł pośredni i oblicz Odległość[][] dla każdej pary węzłów {i,j}, korzystając ze wzoru:

co to jest numer alfabetu

= Odległość[i][j] = minimalna (Odległość[i][j], (Odległość od i do D ) + (Odległość od D do j))
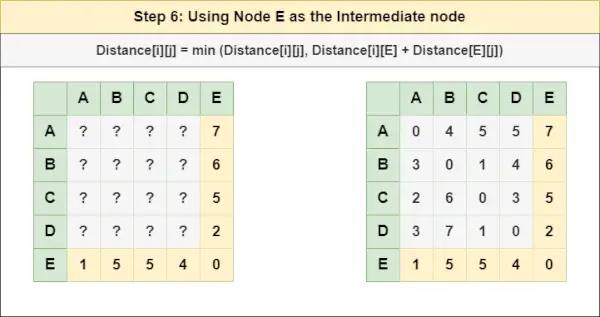
= Odległość[i][j] = minimalna (Odległość[i][j], Odległość[i][ D ] + Odległość [ D ][J])

krok 5 rysowania

Krok 6 : Leczyć węzeł I jako węzeł pośredni i oblicz Odległość[][] dla każdej pary węzłów {i,j}, korzystając ze wzoru:

= Odległość[i][j] = minimalna (Odległość[i][j], (Odległość od i do I ) + (Odległość od I do j))
= Odległość[i][j] = minimalna (Odległość[i][j], Odległość[i][ I ] + Odległość [ I ][J])

krok 6rysuj

Krok 7 : Ponieważ wszystkie węzły zostały potraktowane jako węzeł pośredni, możemy teraz zwrócić zaktualizowaną macierz Odległość[][] jako naszą macierz odpowiedzi.

krok 7 rysowanie
Zalecana praktyka Wypróbuj!

Poniżej implementacja powyższego podejścia:

C++ 
// C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ----> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(odległość[i][k] + odległość[k][j]) && (odległość[k][j] != INF && odległość[i][k] != INF)) odległość[i][j] = odległość [i] [k] + odległość [k] [j];  } } } // Wydrukuj najkrótszą odległość matrix printSolution(dist); } /* Funkcja narzędziowa do drukowania rozwiązania */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 */ int wykres[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, {INF, INF, INF, 0 } };  // Wywołanie funkcji floydWarshall(graph);  zwróć 0; } // Ten kod został stworzony przez Mythri J L>
C 
// C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ----> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 */ int wykres[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, {INF, INF, INF, 0 } };  // Wywołanie funkcji floydWarshall(graph);  zwróć 0; }>
Jawa 
// Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ----> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 */ int wykres[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, {INF, INF, INF, 0 } };  AllPairShortestPath a = nowa AllPairShortestPath();  // Wywołanie funkcji a.floydWarshall(graph);  } } // Autor: Aakash Hasija>
Python3 
# Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ----> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} ''' dla k w zakresie(V): # wybierz wszystkie wierzchołki jeden po drugim jako źródło dla i w range(V): # Wybierz wszystkie wierzchołki jako miejsce docelowe dla # powyżej wybranego źródła j w zakresie(V): # Jeśli wierzchołek k znajduje się na najkrótszej ścieżce od # i do j, zaktualizuj wartość dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Funkcja narzędziowa umożliwiająca wydrukowanie rozwiązania def printSolution (odległość): print('Poniższa macierz pokazuje najkrótsze odległości pomiędzy każdą parą wierzchołków') dla i w zakresie(V): dla j w zakresie(V): if(odległość[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Kod sterownika if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 ''' wykres = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Wywołanie funkcji floydWarshall(graph) # Ten kod jest autorstwa Mythri J L>
C# 
// C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ---> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 */ int[, ] wykres = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, {INF, INF, INF, 0 } };  AllPairShortestPath a = nowa AllPairShortestPath();  // Wywołanie funkcji a.floydWarshall(graph);  } } // Autorem tego artykułu jest // Abdul Mateen Mohammed>
JavaScript 
// A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>nowa tablica(this.V).fill(0));  var i, j, k;  // Zainicjuj macierz rozwiązań // tak samo jak macierz grafów wejściowych // Można też powiedzieć, że początkowe // wartości najmniejszych odległości // opierają się na najkrótszych ścieżkach // nie biorąc pod uwagę żadnego środka pośredniego // wierzchołka dla (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.  ---> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------>(2) 3 */ var graph = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = new AllPairShortestPath();  // Wydrukuj rozwiązanie a.floydWarshall(graph);    // Ten kod pochodzi od rdtaank.>
PHP 
 // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Przed rozpoczęciem iteracji mamy najkrótsze odległości pomiędzy wszystkimi parami wierzchołków, tak że w najkrótszych odległościach tylko wierzchołki ze zbioru {0, 1, 2, .. k-1} są wierzchołkami pośrednimi.   ----> Po zakończeniu iteracji wierzchołek nr. k jest dodawane do zbioru wierzchołków pośrednich i zbiór przyjmuje postać {0, 1, 2, .. k} */ for ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------>(2) 3 */ $wykres = tablica(tablica(0, 5, $INF, 10), tablica($INF, 0, 3, $INF), tablica($ INF, $INF, 0, 1), tablica($INF, $INF, $INF, 0)); // Wywołanie funkcji floydWarshall($graph, $V, $INF); // Ten kod jest dziełem Ryugi?>>
Wyjście 
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Analiza złożoności algorytmu Floyda Warshalla:

  • Złożoność czasowa: O(V3), gdzie V jest liczbą wierzchołków grafu i uruchamiamy trzy zagnieżdżone pętle, każda o rozmiarze V
  • Przestrzeń pomocnicza: O(V2), aby utworzyć macierz 2-D w celu przechowywania najkrótszej odległości dla każdej pary węzłów.

Notatka : Powyższy program drukuje tylko najkrótsze odległości. Możemy zmodyfikować rozwiązanie tak, aby drukowało najkrótsze ścieżki również przechowując informacje o poprzedniku w osobnej matrycy 2D.

Kolejka priorytetowa Java

Dlaczego algorytm Floyda-Warshalla jest lepszy w przypadku gęstych wykresów, a nie w przypadku rzadkich wykresów?

Gęsty wykres : Graf, w którym liczba krawędzi jest znacznie większa niż liczba wierzchołków.
Rzadki wykres : Graf, w którym liczba krawędzi jest bardzo mała.

Niezależnie od tego, ile krawędzi jest w grafie, Algorytm Floyda Warshalla biegnie dla O(V3) razy, dlatego najlepiej nadaje się do Gęste wykresy . W przypadku rzadkich wykresów, Algorytm Johnsona jest bardziej odpowiedni.

  • Jak wykryć cykl ujemny na wykresie za pomocą algorytmu Floyda Warshalla?
  • Czym różni się algorytm Floyda-warshalla od algorytmu Dijkstry?
  • Czym różni się algorytm Floyda-Warshalla od algorytmu Bellmana-Forda?

Zastosowania algorytmu Floyda-Warshalla w świecie rzeczywistym:

  • W sieciach komputerowych algorytm może zostać użyty do znalezienia najkrótszej ścieżki pomiędzy wszystkimi parami węzłów w sieci. Nazywa się to tzw routing sieciowy .
  • Łączność lotów W branży lotniczej, aby znaleźć najkrótszą trasę pomiędzy lotniskami.
  • GIS ( Systemy Informacji Geograficznej ) aplikacje często obejmują analizę danych przestrzennych, takich jak sieci drogowe, w celu znalezienia najkrótszych ścieżek między lokalizacjami.
  • Algorytm Kleene’a które jest uogólnieniem Floyda Warshalla, może być użyte do znalezienia wyrażeń regularnych dla języka regularnego.