Drzewo AVL:
Drzewo AVL jest samobalansującym drzewem wyszukiwania binarnego ( BST ), gdzie różnica wysokości lewego i prawego poddrzewa nie może być większa niż jeden dla wszystkich węzłów.
Przykład drzewa AVL:
Powyższe drzewo to AVL, ponieważ różnice między wysokościami lewego i prawego poddrzewa dla każdego węzła są mniejsze lub równe 1.
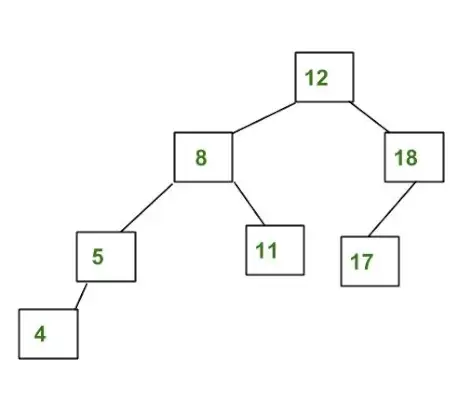
Przykład drzewa, które NIE jest drzewem AVL:

Powyższe drzewo nie jest AVL, ponieważ różnice między wysokościami lewego i prawego poddrzewa dla 8 i 12 są większe niż 1.
Dlaczego drzewa AVL?
Większość operacji BST (np. wyszukiwanie, maks., min., wstawianie, usuwanie.. itp.) jest wykonywana Oh) czas gdzie H jest wysokością BST. Koszt tych operacji może stać się NA) dla przekrzywione drzewo binarne . Jeśli upewnimy się, że wysokość drzewa pozostanie O(log(n)) po każdym dodaniu i usunięciu możemy zagwarantować górną granicę O(log(n)) za wszystkie te operacje. Wysokość drzewa AVL jest zawsze równa O(log(n)) Gdzie N to liczba węzłów w drzewie.
Wprowadzenie w drzewie AVL:
Aby mieć pewność, że dane drzewo pozostanie AVL po każdym wstawieniu, musimy rozszerzyć standardową operację wstawiania BST, aby przeprowadzić pewne ponowne zrównoważenie.
Poniżej znajdują się dwie podstawowe operacje, które można wykonać, aby zrównoważyć BST bez naruszania właściwości BST (klawisze (po lewej)
- Obrót w lewo
- Prawy obrót
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1 i / <- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>Zalecana praktyka Wstawianie drzewa AVL Wypróbuj!
Kroki, które należy wykonać podczas wstawiania:
Niech nowo wstawiony węzeł będzie w
- Wykonaj standardowo BST wstaw dla w .
- Zaczynając od w , udaj się w górę i znajdź pierwszy niezrównoważony węzeł . Pozwalać z będzie pierwszym niezrównoważonym węzłem, I być dziecko z z który pochodzi ze ścieżki w Do z I X być wnuczka z z który pochodzi ze ścieżki w Do z .
- Zrównoważ ponownie drzewo, wykonując odpowiednie obroty na poddrzewie, w którym jest zakorzenione z. Istnieją 4 możliwe przypadki, które należy rozwiązać x, y I z można ułożyć na 4 sposoby.
- Poniżej przedstawiono możliwe 4 układy:
- y jest lewym dzieckiem z, a x jest lewym dzieckiem y (lewy lewy przypadek)
- y jest lewym dzieckiem z, a x jest prawym dzieckiem y (przypadek lewego prawego)
- y jest właściwym dzieckiem z, a x jest właściwym dzieckiem y (prawy prawy przypadek)
- y jest prawym dzieckiem z, a x jest lewym dzieckiem y (prawy lewy przypadek)
Poniżej przedstawiono operacje, które należy wykonać w wyżej wymienionych 4 przypadkach. We wszystkich przypadkach po prostu musimy przywrócić równowagę poddrzewo, w którym jest zakorzenione z a całe drzewo zostaje zrównoważone wraz z wysokością poddrzewa (po odpowiednich obrotach) zakorzenionego z będzie taki sam jak przed włożeniem.
1. Lewa lewa obudowa
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. Lewa prawa obudowa
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. Właściwy prawy przypadek
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. Prawa lewa obudowa
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
Ilustracja przedstawiająca wstawienie w drzewie AVL





Zbliżać się:
Pomysł jest taki, aby zastosować rekurencyjną wstawkę BST, po wstawieniu otrzymujemy wskaźniki do wszystkich przodków jeden po drugim w sposób oddolny. Nie potrzebujemy więc wskaźnika nadrzędnego, aby podróżować w górę. Sam kod rekurencyjny podróżuje w górę i odwiedza wszystkich przodków nowo wstawionego węzła.
Aby wdrożyć pomysł, wykonaj kroki wymienione poniżej:
- Wykonaj normalne Wstawienie BST.
- Bieżący węzeł musi być jednym z przodków nowo wstawionego węzła. Zaktualizuj wysokość bieżącego węzła.
- Uzyskaj współczynnik równowagi (wysokość lewego poddrzewa – wysokość prawego poddrzewa) bieżącego węzła.
- Jeśli współczynnik równowagi jest większy niż 1, wtedy bieżący węzeł jest niezrównoważony i albo jesteśmy w Lewa Lewa obudowa Lub lewy prawy przypadek . Aby sprawdzić, czy tak jest lewa lewa obudowa czy nie, porównaj nowo włożony klucz z kluczem w lewy korzeń poddrzewa .
- Jeśli współczynnik równowagi jest mniejszy niż -1 , to bieżący węzeł jest niezrównoważony i jesteśmy albo w przypadku Prawego Prawego, albo Prawego-Lewego. Aby sprawdzić, czy jest to przypadek Right Right, czy nie, porównaj nowo wstawiony klucz z kluczem w prawym katalogu głównym poddrzewa.
Poniżej implementacja powyższego podejścia:
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->wysokość;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? za: b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->klucz = klucz;> >node->po lewej = NULL;> >node->prawo = NULL;> >node->wysokość = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->lewy;> >Node *T2 = x->Prawidłowy;> > >// Perform rotation> >x->prawo = y;> >y->po lewej = T2;> > >// Update heights> >y->wysokość = max(wysokość(y->lewo),> >height(y->prawo)) + 1;> >x->wysokość = max(wysokość(x->lewo),> >height(x->prawo)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->Prawidłowy;> >Node *T2 = y->lewy;> > >// Perform rotation> >y->lewy = x;> >x->prawo = T2;> > >// Update heights> >x->wysokość = max(wysokość(x->lewo),> >height(x->prawo)) + 1;> >y->wysokość = max(wysokość(y->lewo),> >height(y->prawo)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->po lewej) - wysokość(N->prawa);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->lewy = wstaw(węzeł->lewy, klawisz);> >else> if> (key>węzeł->klucz)> >node->prawo = wstaw(węzeł->prawo, klawisz);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->wysokość = 1 + max(wysokość (węzeł->lewy),> >height(node->Prawidłowy));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && klawisz w lewo->klawisz)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->prawy->klawisz)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 klawisz &&> węzeł->lewy->klawisz)> >{> >node->lewy = lewyRotate(węzeł->lewy);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->klawisz)> >{> >node->prawo = prawoRotate(węzeł->prawo);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->lewy); preOrder(root->right); } } // Kod sterownika int main() { Węzeł *root = NULL; /* Konstruowanie drzewa pokazanego na powyższym rysunku */ root = wstawka(root, 10); root = wstaw(korzeń, 20); root = wstaw(korzeń, 30); root = wstaw(korzeń, 40); root = wstaw(korzeń, 50); root = wstaw(korzeń, 25); /* Skonstruowane drzewo AVL będzie miało postać 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->wysokość;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? za: b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->klucz = klucz;> >node->po lewej = NULL;> >node->prawo = NULL;> >node->wysokość = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->lewy;> >struct> Node *T2 = x->Prawidłowy;> > >// Perform rotation> >x->prawo = y;> >y->po lewej = T2;> > >// Update heights> >y->wysokość = max(wysokość(y->lewo),> >height(y->prawo)) + 1;> >x->wysokość = max(wysokość(x->lewo),> >height(x->prawo)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->Prawidłowy;> >struct> Node *T2 = y->lewy;> > >// Perform rotation> >y->lewy = x;> >x->prawo = T2;> > >// Update heights> >x->wysokość = max(wysokość(x->lewo),> >height(x->prawo)) + 1;> >y->wysokość = max(wysokość(y->lewo),> >height(y->prawo)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->po lewej) - wysokość(N->prawa);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->lewy = wstaw(węzeł->lewy, klawisz);> >else> if> (key>węzeł->klucz)> >node->prawo = wstaw(węzeł->prawo, klawisz);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->wysokość = 1 + max(wysokość (węzeł->lewy),> >height(node->Prawidłowy));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 && klawisz w lewo->klawisz)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->prawy->klawisz)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 klawisz &&> węzeł->lewy->klawisz)> >{> >node->lewy = lewyRotate(węzeł->lewy);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->klawisz)> >{> >node->prawo = prawoRotate(węzeł->prawo);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->klucz);> >preOrder(root->lewy);> >preOrder(root->Prawidłowy);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
>
Jawa
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>B) ? za: b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = wstaw(węzeł.prawo, klucz); else // Duplikowanie kluczy nie jest dozwolone węzeł zwrotny; /* 2. Zaktualizuj wysokość tego węzła-przodka */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Uzyskaj współczynnik równowagi tego węzła nadrzędnego, aby sprawdzić, czy węzeł ten stał się niezrównoważony */ int Balance = getBalance(node); // Jeśli ten węzeł stanie się niezrównoważony, // wystąpią 4 przypadki Lewy Lewy przypadek if (saldo> 1 && klawisz return prawyRotate(węzeł); // Prawy Prawy przypadek if (balans<-1 && key>węzeł.prawy.klucz) return leftRotate(węzeł); // Lewy Prawy Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(node.left); powrót w prawoObróć(węzeł); } // Prawa lewa litera if (balance<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 i klawisz return self.rightRotate(root) # Przypadek 2 - Prawo Prawo w przypadku równowagi<-1 and key>root.right.val: return self.leftRotate(root) # Przypadek 3 - Lewo Prawo, jeśli saldo> 1 i klucz> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root ) # Przypadek 4 – Prawa, lewa, jeśli równowaga<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>B) ? za: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = wstaw(węzeł.prawo, klucz); else // Duplikowanie kluczy nie jest dozwolone węzeł zwrotny; /* 2. Zaktualizuj wysokość tego węzła-przodka */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Uzyskaj współczynnik równowagi tego węzła nadrzędnego, aby sprawdzić, czy węzeł ten stał się niezrównoważony */ int Balance = getBalance(node); // Jeśli ten węzeł stanie się niezrównoważony, to // będą 4 przypadki Lewy Lewy Case if (saldo> 1 && klawisz return RightRotate(node); // Prawy Prawy Case if (równowaga węzeł.prawy.klawisz) return leftRotate(węzeł) ; // Lewy Prawy przypadek if (balans> 1 && klucz> węzeł.left.key) { node.left = leftRotate(node.left); return RightRotate(node); } // Prawy Lewy przypadek if (balance<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
JavaScript
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>B ? za: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = this.insert(węzeł.prawo, klucz); // Duplikowanie kluczy nie jest dozwolone, w przeciwnym razie zwróć węzeł; /* 2. Zaktualizuj wysokość tego węzła-przodka */ node.height = 1 + this.max(this.height(node.left), this.height(node.right)); /* 3. Uzyskaj współczynnik równowagi tego węzła nadrzędnego, aby sprawdzić, czy węzeł ten stał się niezrównoważony */ var Balance = this.getBalance(node); // Jeśli ten węzeł stanie się niezrównoważony, to // wystąpią 4 przypadki Lewy Lewy przypadek if (saldo> 1 && klawisz return this.rightRotate(node); // Prawy Prawy przypadek if (balance node.right.key) zwróć to. leftRotate(node); // Lewy Prawy Case if (balans> 1 && klucz> węzeł.left.key) { node.left = this.leftRotate(node.left); return this.rightRotate(node); Lewa litera if (balans<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>Wyjście
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
Analiza złożoności
Złożoność czasowa: O(log(n)), do wstawienia
Przestrzeń pomocnicza: O(1)
wskaźnik dereferencji c
Operacje obrotu (obrót w lewo i w prawo) zajmują stały czas, ponieważ zmienia się tam tylko kilka wskaźników. Aktualizacja wysokości i uzyskanie współczynnika równowagi również zajmuje dużo czasu. Zatem złożoność czasowa wstawki AVL pozostaje taka sama jak wstawki BST, która wynosi O(h), gdzie h jest wysokością drzewa. Ponieważ drzewo AVL jest zrównoważone, wysokość wynosi O(Logn). Zatem złożoność czasowa wstawki AVL wynosi O(Logn).
Porównanie z czerwonym czarnym drzewem:
Drzewo AVL i inne samobalansujące się drzewa wyszukiwania, takie jak Red Black, są przydatne do wykonywania wszystkich podstawowych operacji w czasie O(log n). Drzewa AVL są bardziej zrównoważone w porównaniu do drzew czerwono-czarnych, ale mogą powodować więcej rotacji podczas wstawiania i usuwania. Jeśli więc Twoja aplikacja wymaga wielu częstych wstawień i usunięć, preferowane powinny być drzewa czerwono-czarne. A jeśli wstawienia i usunięcia są rzadsze, a wyszukiwanie jest częstszą operacją, wówczas drzewo AVL powinno być preferowane zamiast drzewa Red Black Tree.
Poniżej znajduje się post do usunięcia w drzewie AVL:
Drzewo AVL | Zestaw 2 (usunięcie)
