Dawać BST , zadaniem jest przeszukanie węzła w tym BST .
Aby wyszukać wartość w BST, rozważ ją jako posortowaną tablicę. Teraz możemy łatwo przeprowadzić operację wyszukiwania w BST za pomocą Algorytm wyszukiwania binarnego .
Algorytm wyszukiwania klucza w danym drzewie wyszukiwania binarnego:
Załóżmy, że chcemy wyszukać numer X, Zaczynamy od korzenia. Następnie:
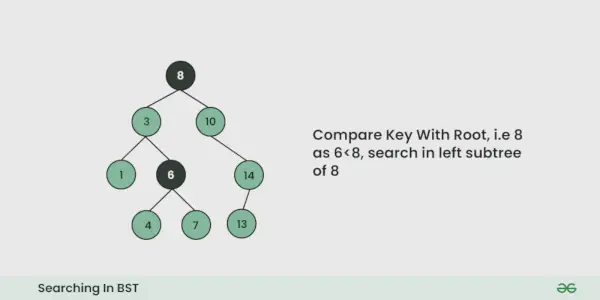
- Porównujemy szukaną wartość z wartością pierwiastka.
- Jeśli jest równa, kończymy wyszukiwanie, jeśli jest mniejsze, wiemy, że musimy przejść do lewego poddrzewa, ponieważ w drzewie wyszukiwania binarnego wszystkie elementy w lewym poddrzewie są mniejsze, a wszystkie elementy w prawym poddrzewie są większe.
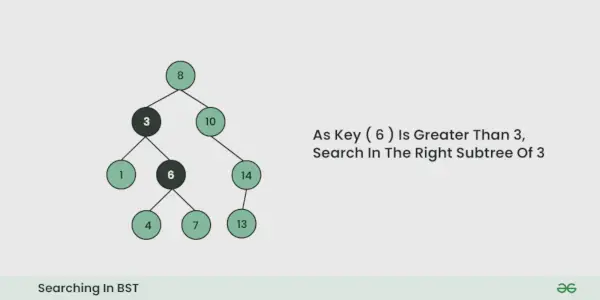
- Powtarzaj powyższy krok, aż dalsze przejście nie będzie możliwe
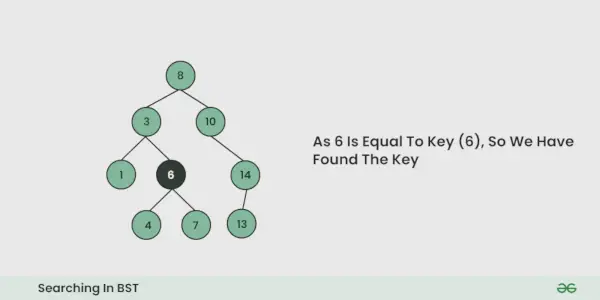
- Jeśli w dowolnej iteracji zostanie znaleziony klucz, zwróć wartość True. Inaczej Fałsz.
Ilustracja wyszukiwania w BST:
Aby lepiej zrozumieć, zobacz poniższą ilustrację:
kod abs-c
Zalecana praktykaWyszukaj węzeł w BSTWypróbuj!
Program do implementacji wyszukiwania w BST:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->klucz = element;> >temp->lewy = temp->prawy = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->lewy = wstaw(węzeł->lewy, klawisz);> >else> if> (key>węzeł->klucz)> >node->prawo = wstaw(węzeł->prawo, klawisz);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
C
strsep c
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->klucz = element;> >temp->lewy = temp->prawy = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->lewy = wstaw(węzeł->lewy, klawisz);> >else> if> (key>węzeł->klucz)> >node->prawo = wstaw(węzeł->prawo, klawisz);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
>
Jawa
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = wstaw(węzeł.prawo, klucz); // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędzia do wyszukiwania klucza w wyszukiwaniu węzła BST (główny węzeł, int klucz) // Kod sterownika public static void main(String[] args) { Drzewo BinarySearchTree = new BinarySearchTree(); // Wstawianie węzłów drzewo.root = drzewo.insert(drzewo.root, 50); drzewo.wstaw(drzewo.korzeń, 30); drzewo.wstaw(drzewo.korzeń, 20); drzewo.wstaw(korzeń drzewa, 40); drzewo.wstaw(korzeń drzewa, 70); drzewo.wstaw(korzeń drzewa, 60); drzewo.wstaw(drzewo.korzeń, 80); // Znaleziony klucz int klucz = 6; // Wyszukiwanie w BST if (tree.search(tree.root, key) == null) System.out.println(key + ' nie znaleziono'); else System.out.println(klucz + ' znaleziony'); klucz = 60; // Wyszukiwanie w BST if (tree.search(tree.root, key) == null) System.out.println(key + ' nie znaleziono'); else System.out.println(klucz + ' znaleziony'); } }> |
>
>
Python3
stos w Javie
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>node.key: node.right = wstaw(node.right, key) # Zwraca (niezmieniony) wskaźnik węzła return node # Funkcja narzędziowa do wyszukiwania klucza w BST def search(root, key): # Przypadki podstawowe: root is null lub klucz jest obecny w katalogu głównym, jeśli root to None lub root.key == klucz: return root # Klucz jest większy niż klucz root, jeśli root.key return search(root.right, key) # Klucz jest mniejszy niż root klawisz ' return search(root.left, key) # Kod sterownika if __name__ == '__main__': root = Brak root = wstaw(root, 50) wstaw(root, 30) wstaw(root, 20) wstaw (root, 40) wstaw(root, 70) wstaw(root, 60) wstaw(root, 80) # Klucz do znalezienia klucz = 6 # Wyszukiwanie w BST, jeśli search(root, klucz) ma wartość Brak: print(key, 'nie znaleziono') else: print(klucz, 'znaleziono') key = 60 # Wyszukiwanie w BST, jeśli search(root, klucz) to Brak: print(klucz, 'nie znaleziono') else: print(key, 'znaleziono')> |
>
>
C#
polecenie instalacji npm
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = Wstaw(węzeł.prawo, klucz); // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędzia do wyszukiwania klucza w publicznym przeszukiwaniu węzła BST (korzeń węzła, klucz int) // Przypadki podstawowe: root ma wartość null lub klucz jest obecny w katalogu głównym if (root == null // Kod sterownika public static void Main () { Korzeń węzła = null; Drzewo binarne bt = nowe drzewo binarne(); root = bt.Insert(root, 50); bt.Insert(root, 20); , 40); bt.Insert(root, 70); bt.Insert(root, 60); bt.Insert(root, 80); // Klucz do znalezienia int klucz = 6; // Wyszukiwanie w BST if ( bt.Search(root, klucz) == null) Console.WriteLine(key + ' nie znaleziono'); else Console.WriteLine(key + ' znaleziono'); // Wyszukiwanie w BST if (bt.Search(root, klucz) == null) Console.WriteLine(key + ' nie znaleziono'); else Console.WriteLine(key + ' znaleziono'); |
>zmienna referencyjna w Javie
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędziowa do wyszukiwania klucza w funkcji BST search(root, key) { // Przypadki podstawowe: root ma wartość null lub klucz jest obecny w katalogu głównym if (root === null || root.key === klucz ) {zwróć korzeń; } // Klucz jest większy niż klucz roota if (root.key return search(root.right, key); } // Klucz jest mniejszy niż klucz roota return search(root.left, key); } // Kod sterownika let root = null; wstaw (korzeń, 50); wstaw (korzeń, 20); wstaw (korzeń, 40); 60); wstaw(root, 80); // Znaleziono klucz niech klucz = 6; // Wyszukiwanie w BST if (search(root, klucz) === null) { console.log(key + ' not znaleziony'); } else { console.log(key + ' znaleziony' } key = 60; // Wyszukiwanie w BST if (search(root, klucz) === null) { console.log( klucz + ' nie znaleziono'); else { konsola.log(klucz + ' znaleziono');>6 not found 60 found> Złożoność czasowa: O(h), gdzie h jest wysokością BST.
Przestrzeń pomocnicza: O(h), gdzie h jest wysokością BST. Dzieje się tak, ponieważ maksymalna ilość miejsca potrzebna do przechowywania stosu rekurencji będzie wynosić H .Powiązane linki:
- Operacja wstawiania drzewa wyszukiwania binarnego
- Operacja usuwania drzewa wyszukiwania binarnego