Drzewo wyszukiwania binarnego to struktura danych stosowana w informatyce do porządkowania i przechowywania danych w sposób posortowany. Drzewo wyszukiwania binarnego podąża za wszystkimi właściwościami drzewa binarnego i jego właściwości lewy dziecko zawiera wartości mniejsze niż węzeł nadrzędny i Prawidłowy dziecko zawiera wartości większe niż węzeł nadrzędny. Ta hierarchiczna struktura pozwala na efektywność Badawczy , Wprowadzenie , I Usunięcie operacje na danych przechowywanych w drzewie.
Drzewo wyszukiwania binarnego
Spis treści
if else pętla w Javie
- Co to jest drzewo wyszukiwania binarnego?
- Właściwości drzewa wyszukiwania binarnego
- Obsługa zduplikowanych wartości w drzewie wyszukiwania binarnego
- Operacje wykonywane na BST
- 1. Wyszukiwanie węzła w BST
- 2. Wstaw węzeł do BST
- 3. Usuń węzeł BST
- 4. Traversal (inorderowe przejście BST)
- Zastosowania BST
- Zalety
- Niedogodności
- FAQ (często zadawane pytania) dotyczące drzewa wyszukiwania binarnego:
Co to jest drzewo wyszukiwania binarnego?
Drzewo wyszukiwania binarnego (BST) jest szczególnym typem drzewo binarne w którym lewe dziecko węzła ma wartość mniejszą niż wartość węzła, a prawe dziecko ma wartość większą niż wartość węzła. Właściwość ta nazywana jest właściwością BST i umożliwia efektywne wyszukiwanie, wstawianie i usuwanie elementów w drzewie.
Właściwości drzewa wyszukiwania binarnego:
- Lewe poddrzewo węzła zawiera tylko węzły z kluczami mniejszymi niż klucz węzła.
- Prawe poddrzewo węzła zawiera tylko węzły z kluczami większymi niż klucz węzła.
- Oznacza to, że wszystko na lewo od pierwiastka jest mniejsze niż wartość pierwiastka, a wszystko na prawo od pierwiastka jest większe niż wartość pierwiastka. Dzięki temu wyszukiwanie binarne jest bardzo łatwe.
- Każde lewe i prawe poddrzewo musi być również drzewem wyszukiwania binarnego.
- Nie może być żadnych zduplikowanych węzłów (BST może mieć zduplikowane wartości przy różnych podejściach do obsługi)
Obsługa zduplikowanych wartości w drzewie wyszukiwania binarnego:
- Musimy przestrzegać spójnego procesu, tj. przechowywać zduplikowaną wartość po lewej stronie lub przechowywać zduplikowaną wartość po prawej stronie elementu głównego, ale należy zachować zgodność ze swoim podejściem.
Podstawowe operacje na drzewie wyszukiwania binarnego:
1. Wyszukiwanie węzła w BST:
Wyszukiwanie w BST oznacza zlokalizowanie określonego węzła w strukturze danych. W drzewie wyszukiwania binarnego przeszukiwanie węzła jest łatwe ze względu na jego określoną kolejność. Etapy wyszukiwania węzła w drzewie wyszukiwania binarnego są następujące –
- Najpierw porównaj element, który ma być przeszukany, z elementem głównym drzewa.
- Jeśli do elementu docelowego pasuje element główny, zwróć lokalizację węzła.
- Jeśli nie jest dopasowany, to sprawdź, czy element jest mniejszy od elementu głównego, jeśli jest mniejszy od elementu głównego, to przejdź do lewego poddrzewa.
- Jeśli jest większy niż element główny, przejdź do prawego poddrzewa.
- Powtarzaj powyższą procedurę rekurencyjnie, aż zostanie znalezione dopasowanie.
- Jeżeli element nie zostanie odnaleziony lub nie występuje w drzewie, zwróć NULL.
Teraz zrozummy wyszukiwanie w drzewie binarnym na przykładzie:
Poniżej podano BST i musimy szukać elementu 6.
ciąg znaków Java.format
Kod:
Poniżej implementacja wyszukiwania w BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja narzędziowa umożliwiająca wstawienie // nowego węzła o podanym kluczu w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL ) zwróć nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) węzeł->lewy = wstaw(węzeł->lewy, klawisz); else if (klucz> węzeł->klucz) węzeł->prawy = wstaw(węzeł->prawy, klucz); // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędziowa do wyszukiwania klucza w BST struct węzeł* search(węzeł struct* root, int klucz) root->key == klucz) return root; // Klucz jest większy niż klucz roota if (root->key< key) return search(root->prawda, klucz); // Klucz jest mniejszy niż klucz powrotu roota (root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja narzędziowa umożliwiająca wstawienie // nowego węzła o podanym kluczu w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL ) zwróć nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) węzeł->lewy = wstaw(węzeł->lewy, klucz); else if (klucz> węzeł->klucz) węzeł->prawy = wstaw(węzeł->prawy, klucz); // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędziowa do wyszukiwania klucza w węźle BST struct node* search(węzeł struct* root, int klucz)> Jawa // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>węzeł.klucz) węzeł.prawo = wstaw(węzeł.prawo, klucz); // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędziowa do wyszukiwania klucza w wyszukiwaniu węzła BST (root węzła, int klucz) // Przypadki podstawowe: root ma wartość null lub klucz jest obecny w katalogu głównym if (root == null> Pyton # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = wstaw(node.right, key) # Zwraca (niezmieniony) wskaźnik węzła return node # Funkcja narzędziowa do wyszukiwania klucza w BST def search(root, key): # Przypadki podstawowe: root is null lub klucz jest obecny w katalogu głównym, jeśli root ma wartość None lub root.key == klucz: return root # Klucz jest większy niż klucz roota, jeśli root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca (niezmieniony) wskaźnik węzła; zwraca węzeł; } // Funkcja narzędziowa do wyszukiwania klucza w funkcji BST search(root, key) { // Przypadki podstawowe: root ma wartość null lub klucz jest obecny w katalogu głównym if (root === null || root.key === klucz ) {zwróć korzeń; } // Klucz jest większy niż klucz roota if (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Wstaw węzeł do BST :
Do skrzydła zawsze wkładany jest nowy klucz. Rozpocznij wyszukiwanie klucza od korzenia do węzła liścia. Po znalezieniu węzła liścia nowy węzeł jest dodawany jako element podrzędny węzła liścia.
Kod:
Poniżej znajduje się implementacja wstawienia pojedynczego węzła do drzewa wyszukiwania binarnego:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klucz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klucz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; }> Jawa class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca węzeł return węzeł; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = wstaw(node.right, key) # Zwraca wskaźnik węzła return node>
JavaScript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca wskaźnik węzła return node; }> Złożoność czasowa: O(N), gdzie N jest liczbą węzłów BST
Przestrzeń pomocnicza: O(1)
3. Usuń węzeł BST :
Służy do usunięcia węzła z określonym kluczem z BST i zwrócenia nowego BST.
Różne scenariusze usuwania węzła:
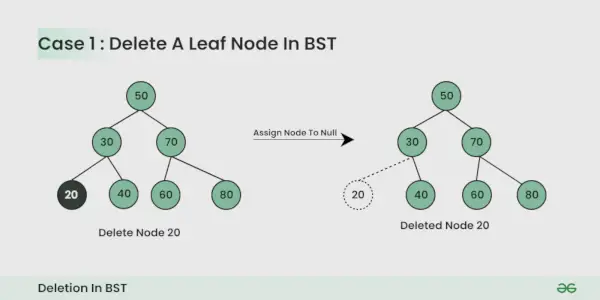
Węzeł do usunięcia to węzeł liścia :
To proste, możesz to po prostu wyzerować.
wersje Androida
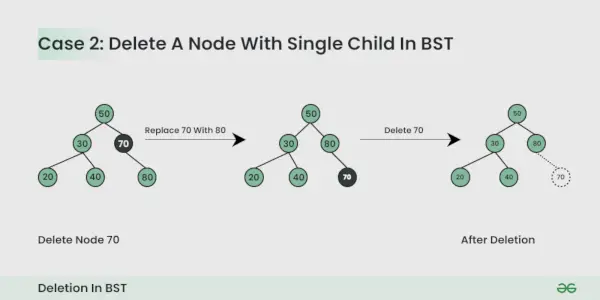
Węzeł do usunięcia ma jedno dziecko :
Możesz po prostu zastąpić węzeł węzłem podrzędnym.
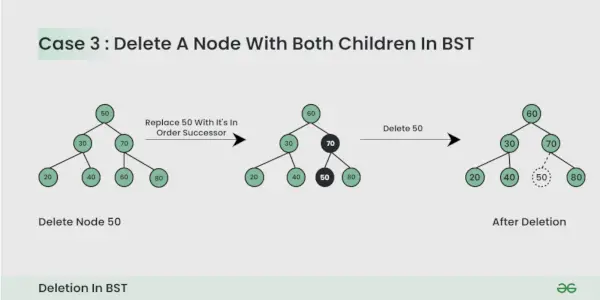
Węzeł do usunięcia ma dwoje dzieci :
Tutaj musimy usunięcie węzła odbywa się w taki sposób, aby powstałe drzewo było zgodne z właściwościami BST. Sztuka polega na znalezieniu inorderowego następcy węzła. Skopiuj zawartość inorderowego następnika węzła i usuń inorder następcę.
Podczas usuwania węzła BST zadbaj o następujące rzeczy:
- Trzeba dowiedzieć się, co zastąpi węzeł, który ma zostać usunięty.
- Chcesz minimalnych zakłóceń w istniejącej strukturze drzewa
- Może pobrać węzeł zastępczy z lewego lub prawego poddrzewa usuniętych węzłów.
- Jeśli bierzemy if z lewego poddrzewa, musimy przyjąć największą wartość z lewego poddrzewa.
- Jeśli bierzemy if z prawego poddrzewa, musimy przyjąć najmniejszą wartość z prawego poddrzewa.
Kod:
Poniżej implementacja usunięcia w BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klucz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; } // Funkcja zwracająca węzeł z minimalną // wartością klucza znalezioną w tym drzewie struct node* minValueNode(struct node* node) { struct node* current = node; // Wykonaj pętlę w dół, aby znaleźć liść znajdujący się najbardziej na lewo, while (bieżący && bieżący->lewy != NULL) bieżący = bieżący->lewy; prąd zwrotny; } // Funkcja usuwająca klucz i // zwracająca nowy główny węzeł struktury* DeleteNode(węzeł struktury* root, int klucz) { // Przypadek bazowy if (root == NULL) return root; // Jeśli klucz do usunięcia jest // mniejszy niż klucz roota, // to leży w lewym poddrzewie if (key< root->klucz) { root->left = DeleteNode(root->left, key); } // Jeśli klucz do usunięcia jest // większy niż klucz roota, // to leży w prawym poddrzewie else if (key> root->key) { root->right = DeleteNode(root-> prawda, klucz); } // Jeśli klucz jest taki sam jak klucz roota, // to jest to węzeł // do usunięcia else { // Węzeł z tylko jednym dzieckiem // lub bez dziecka if (root->left == NULL) { węzeł struktury* temp = root->right; darmowy (root); temperatura powrotu; } else if (root->right == NULL) { węzeł struktury* temp = root->left; darmowy (root); temperatura powrotu; } // Węzeł z dwójką dzieci: // Pobierz następcę inorder (najmniejszy // w prawym poddrzewie) struct node* temp = minValueNode(root->right); // Skopiuj zawartość // następnika inorder do tego węzła root->key = temp->key; // Usuń następcę inorder root->right = DeleteNode(root->right, temp->key); } zwróć korzeń; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klucz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; } // Funkcja zwracająca węzeł z minimalną // wartością klucza znalezioną w tym drzewie struct node* minValueNode(struct node* node) { struct node* current = node; // Wykonaj pętlę w dół, aby znaleźć liść znajdujący się najbardziej na lewo, while (bieżący && bieżący->lewy != NULL) bieżący = bieżący->lewy; prąd zwrotny; } // Funkcja usuwająca klucz i // zwracająca nowy główny węzeł struktury* DeleteNode(węzeł struktury* root, int klucz) { // Przypadek bazowy if (root == NULL) return root; // Jeśli klucz do usunięcia jest // mniejszy niż klucz roota, // to leży w lewym poddrzewie if (key< root->klucz) { root->left = DeleteNode(root->left, key); } // Jeśli klucz do usunięcia jest // większy niż klucz roota, // to leży w prawym poddrzewie else if (key> root->key) { root->right = DeleteNode(root-> prawda, klucz); } // Jeśli klucz jest taki sam jak klucz roota, // to jest to węzeł // do usunięcia else { // Węzeł z tylko jednym dzieckiem // lub bez dziecka if (root->left == NULL) { węzeł struktury* temp = root->right; darmowy (root); temperatura powrotu; } else if (root->right == NULL) { węzeł struktury* temp = root->left; darmowy (root); temperatura powrotu; } // Węzeł z dwójką dzieci: // Pobierz następcę inorder (najmniejszy // w prawym poddrzewie) struct node* temp = minValueNode(root->right); // Skopiuj zawartość // następnika inorder do tego węzła root->key = temp->key; // Usuń następcę inorder root->right = DeleteNode(root->right, temp->key); } zwróć korzeń; }> Jawa // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca węzeł return węzeł; } // Funkcja zwracająca węzeł z minimalną // wartością klucza znalezioną w tym drzewie static node minValueNode(node node) { node current = node; // Wykonaj pętlę w dół, aby znaleźć liść znajdujący się najbardziej na lewo, while (current != null && current.left != null) current = current.left; prąd zwrotny; } // Funkcja usuwająca klucz i // zwracająca nowy korzeń statyczny węzeł DeleteNode(node root, int key) { // base Case if (root == null) return root; // Jeśli klucz do usunięcia jest // mniejszy niż klucz roota, // to leży w lewym poddrzewie if (key< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = usuńNode(root.right, klucz); } // Jeśli klucz jest taki sam jak klucz roota, // to jest to węzeł // do usunięcia else { // Węzeł z tylko jednym dzieckiem // lub bez dziecka if (root.left == null) { temperatura węzła = root.right; temperatura powrotu; } else if (root.right == null) { temp węzła = root.left; temperatura powrotu; } // Węzeł z dwójką dzieci: // Uzyskaj następcę w kolejności (najmniejszy // w prawym poddrzewie) węzeł temp = minValueNode(root.right); // Skopiuj // zawartość następnego następnika do tego węzła root.key = temp.key; // Usuń następcę kolejności root.right = DeleteNode(root.right, temp.key); } zwróć korzeń; }> Pyton # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = wstaw(root.right, klucz) # Zwraca wskaźnik węzła return root # Funkcja wykonująca przechodzenie w kolejności BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funkcja zwracająca węzeł z minimalną # wartością klucza znalezioną w tym drzewie def minValueNode(node): current = node # Wykonaj pętlę w dół, aby znaleźć liść znajdujący się najbardziej na lewo, gdy bieżący i current.left nie jest None: current = current.left return current # Funkcja usuwająca klucz i # zwracająca nowy root def DeleteNode(root, key): # base Case jeśli root to None: return root # Jeśli klucz ma być usunięty jest # mniejszy niż klucz główny, # wówczas leży w lewym poddrzewie, jeśli jest kluczem< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = DeleteNode(root.right, key) # Jeśli klucz jest taki sam jak klucz roota, # to jest to węzeł # do usunięcia w innym przypadku: # Węzeł z tylko jednym dzieckiem # lub bez dziecka jeśli root.left ma wartość Brak: temp = root.right root = Brak zwraca temp elif root.right ma wartość Brak: temp = root.left root = Brak zwraca temp # Węzeł z dwójką dzieci: # Uzyskaj następcę kolejności (najmniejszy # w prawe poddrzewo) temp = minValueNode(root.right) # Skopiuj zawartość # następnika inorder do tego węzła root.key = temp.key # Usuń następcę inorder root.right = DeleteNode(root.right, temp.key) zwróć root>
4. Traversal (inorderowe przejście BST) :
W przypadku drzew wyszukiwania binarnego (BST) przechodzenie Inorder daje węzły w kolejności niemalejącej. Najpierw odwiedzamy lewe dziecko, potem korzeń, a na końcu prawe dziecko.
Poniżej znajduje się implementacja sposobu wykonywania przechodzenia w kolejności binarnej drzewa wyszukiwania:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klawisz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; } // Funkcja wykonująca przejście w kolejności BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->klucz; inorder(root->right); } } // Kod sterownika int main() { /* Utwórzmy następujące BST 50 / 30 70 / / 20 40 60 80 */ węzeł struktury* root = NULL; // Tworzenie BST root = wstawka(root, 50); wstaw(korzeń, 30); wstaw(korzeń, 20); wstaw(korzeń, 40); wstaw(korzeń, 70); wstaw(korzeń, 60); wstaw(korzeń, 80); // Wywołanie funkcji inorder(root); zwróć 0; } // Ten kod pochodzi od shivanishinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->klucz = przedmiot; temp->lewo = temp->prawo = NULL; temperatura powrotu; } // Funkcja wstawiająca nowy węzeł z // podanym kluczem w BST struct node* wstaw(struct node* node, int key) { // Jeśli drzewo jest puste, zwróć nowy węzeł if (node == NULL) return nowyWęzeł(klucz); // W przeciwnym razie wróć w dół drzewa if (key< node->klucz) { węzeł->lewy = wstaw(węzeł->lewy, klucz); } else if (klawisz> węzeł->klucz) { węzeł->prawo = wstaw(węzeł->prawo, klawisz); } // Zwraca wskaźnik węzła return node; } // Funkcja wykonująca przejście w kolejności BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->key); inorder(root->right); } } // Kod sterownika int main() { /* Utwórzmy następujące BST 50 / 30 70 / / 20 40 60 80 */ węzeł struktury* root = NULL; // Tworzenie BST root = wstawka(root, 50); wstaw(korzeń, 30); wstaw(korzeń, 20); wstaw(korzeń, 40); wstaw(korzeń, 70); wstaw(korzeń, 60); wstaw(korzeń, 80); // Wywołanie funkcji inorder(root); zwróć 0; }> Jawa import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>węzeł.klucz) { węzeł.prawy = wstaw(węzeł.prawy, klucz); } // Zwraca węzeł return węzeł; } // Funkcja wykonująca przejście w kolejności uporządkowanej statycznej pustki BST inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // Kod sterownika public static void main(String[] args) { /* Utwórzmy następujący BST 50 / 30 70 / / 20 40 60 80 */ root węzła = null; // wstawienie wartości 50 root = wstaw(root, 50); // wstawienie wartości 30 wstaw(root, 30); // wstawienie wartości 20 wstaw(root, 20); // wstawienie wartości 40 wstaw(root, 40); // wstawienie wartości 70 wstaw(root, 70); // wstawienie wartości 60 wstaw(root, 60); // wstawienie wartości 80 wstaw(root, 80); // wypisz kolejność BST (root); } } // Ten kod został napisany przez abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = wstaw(node.right, key) # Zwraca wskaźnik węzła zwracający węzeł # Funkcja wykonująca przechodzenie w kolejności BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Kod sterownika if __name__ == '__main__': # Stwórzmy następujący BST # 50 # / # 30 70 # / / # 20 40 60 80 root = Brak # Tworzenie BST root = wstawka(korzeń, 50) wstawka(korzeń, 30) wstawka(korzeń, 20) wstawka(korzeń, 40) wstawka(korzeń, 70) wstawka(korzeń, 60) wstawka(korzeń , 80) # Wywołanie funkcji inorder(root) #Ten kod został napisany przez japmeet01>
Wyjście
20 30 40 50 60 70 80>
Złożoność czasowa: O(N), gdzie N jest liczbą węzłów BST
Przestrzeń pomocnicza: O(1)
co sprawia, że komputer jest szybki
Zastosowania BST:
- Algorytmy wykresów: BST można wykorzystać do implementacji algorytmów grafowych, na przykład algorytmów minimalnego drzewa rozpinającego.
- Kolejki priorytetowe: BST można wykorzystać do implementacji kolejek priorytetowych, gdzie element o najwyższym priorytecie znajduje się w korzeniu drzewa, a elementy o niższym priorytecie są przechowywane w poddrzewach.
- Samobalansujące drzewo wyszukiwania binarnego: BST mogą być używane jako samobalansujące struktury danych, takie jak drzewo AVL i drzewo czerwono-czarne.
- Przechowywanie i pobieranie danych: BST można wykorzystać do szybkiego przechowywania i wyszukiwania danych, na przykład w bazach danych, gdzie wyszukiwanie określonego rekordu może odbywać się w czasie logarytmicznym.
Zalety:
- Szybkie wyszukiwanie: Wyszukiwanie określonej wartości w BST ma średnią złożoność czasową O (log n), gdzie n to liczba węzłów w drzewie. Jest to znacznie szybsze niż wyszukiwanie elementu w tablicy lub połączonej liście, które w najgorszym przypadku mają złożoność czasową O(n).
- Przechodzenie w kolejności: BST można przechodzić w kolejności, która odwiedza lewe poddrzewo, korzeń i prawe poddrzewo. Można tego użyć do sortowania zbioru danych.
- Oszczędność miejsca: BST zajmują mało miejsca, ponieważ nie przechowują żadnych zbędnych informacji, w przeciwieństwie do tablic i list połączonych.
Niedogodności:
- Przekrzywione drzewa: Jeśli drzewo zostanie przekrzywione, złożoność czasowa operacji wyszukiwania, wstawiania i usuwania będzie wynosić O(n) zamiast O(log n), co może sprawić, że drzewo będzie nieefektywne.
- Wymagany dodatkowy czas: Drzewa samorównoważące wymagają dodatkowego czasu na utrzymanie równowagi podczas operacji wstawiania i usuwania.
- Efektywność: BST nie są wydajne w przypadku zestawów danych z wieloma duplikatami, ponieważ marnują miejsce.
Często zadawane pytania(Często Zadawane Pytania)w drzewie wyszukiwania binarnego:
1. Co to jest drzewo wyszukiwania binarnego?
Drzewo wyszukiwania binarnego (BST) to drzewo binarne, w którym każdy węzeł w lewym poddrzewie jest mniejszy od korzenia, a każdy węzeł w prawym poddrzewie ma wartość większą niż pierwiastek . Właściwości drzewa wyszukiwania binarnego są rekurencyjne: jeśli uznamy dowolny węzeł za pierwiastek, właściwości te pozostaną prawdziwe.
2. Na czym polega operacja drzewa wyszukiwania binarnego?
Istnieją trzy główne operacje w drzewie wyszukiwania binarnego: 1. Wstawienie, 2. Usunięcie, 3. Wyszukiwanie. Ze względu na swoje właściwości efektywne jest przeszukiwanie dowolnego elementu w drzewie wyszukiwania binarnego.
3. Co to jest drzewo wyszukiwania binarnego i drzewo AVL?
Drzewo wyszukiwania binarnego : Drzewo wyszukiwania binarnego (BST) to drzewo binarne, w którym każdy węzeł w lewym poddrzewie jest mniejszy niż pierwiastek, a każdy węzeł w prawym poddrzewie ma wartość większą niż pierwiastek.
Drzewo AVL : Drzewa wyszukiwania binarnego (BST), które automatycznie się równoważą i obracają, nazywane są drzewami AVL.
4. Jakie są zastosowania drzewa wyszukiwania binarnego?
Drzewa wyszukiwania binarnego można wykorzystać do implementacji abstrakcyjnych typów danych, takich jak zestawy dynamiczne, tablice przeglądowe i kolejki priorytetowe, i używane w algorytmy sortowania takie jak sortowanie drzew.
5. Jaka jest różnica pomiędzy drzewem wyszukiwania binarnego a drzewem binarnym?
Drzewo wyszukiwania binarnego to drzewo, które przestrzega określonego porządku rozmieszczenia elementów, podczas gdy drzewo binarne nie ma żadnego porządku.
Powiązane artykuły:
- Zastosowanie BST
- Zastosowania, zalety i wady drzewa wyszukiwania binarnego
- Wstawienie do drzewa wyszukiwania binarnego (BST)
- Wyszukiwanie w drzewie wyszukiwania binarnego (BST)
- Usuwanie w drzewie wyszukiwania binarnego (BST)
