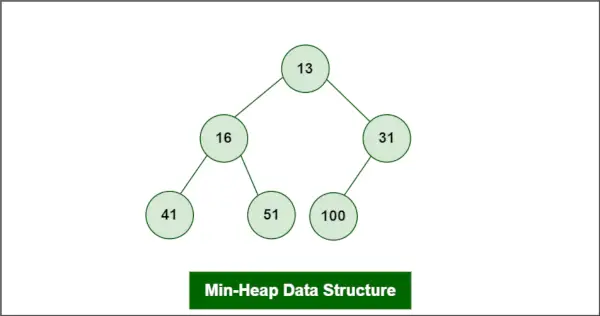
A Min-Sterta jest zdefiniowany jako rodzaj Struktura danych sterty to rodzaj drzewa binarnego powszechnie stosowanego w informatyce do różnych celów, w tym do sortowania, wyszukiwania i organizowania danych.
Wprowadzenie do Min-Heap – samouczki dotyczące struktury danych i algorytmów
Cel i przypadki użycia Min-Heap:
- Implementacja kolejki priorytetowej: Jednym z głównych zastosowań struktury danych sterty jest implementacja kolejek priorytetowych.
- Algorytm Dijkstry : Algorytm Dijkstry to algorytm najkrótszej ścieżki, który znajduje najkrótszą ścieżkę między dwoma węzłami na grafie. Minimalna sterta może służyć do śledzenia nieodwiedzonych węzłów znajdujących się w najmniejszej odległości od węzła źródłowego.
- Sortowanie: Min sterty można użyć jako algorytmu sortowania, aby efektywnie sortować zbiór elementów w porządku rosnącym.
- Mediana wyniku: Aby skutecznie znaleźć medianę strumienia liczb, można użyć minimalnej sterty. Możemy użyć jednej minimalnej sterty do przechowywania większej połowy liczb i jednej maksymalnej sterty do przechowywania mniejszej połowy. Mediana będzie korzeniem sterty min.
Struktura danych Min-Heap w różnych językach:
1. Min-Heap w C++
Minimalną stertę można zaimplementować za pomocą metody kolejka priorytetowa kontener ze standardowej biblioteki szablonów (STL). The kolejka priorytetowa kontener to typ adaptera kontenera, który umożliwia przechowywanie elementów w strukturze danych przypominającej kolejkę, w której każdy element ma przypisany priorytet.
Składnia :
C++ priority_queue < int, vector , większy > minH;>
2. Min-Heap w Javie
W Javie stertę min można zaimplementować za pomocą metody Kolejka priorytetowa klasa od pakiet java.util . Klasa PriorityQueue to kolejka priorytetowa, która umożliwia przechowywanie elementów w strukturze danych przypominającej kolejkę, w której każdy element ma powiązany z nim priorytet.
Składnia :
Jawa PriorityQueue minHeap = nowa kolejka priorytetów ();>
3. Min-Heap w Pythonie
W Pythonie mini stertę można zaimplementować za pomocą metody sterta moduł, który udostępnia funkcje implementujące sterty. Konkretnie, sterta moduł zapewnia sposób tworzenia i manipulowania strukturami danych sterty.
Składnia:
Pyton heap = [] heapify(heap)>
4. Min-Heap w C#
W języku C# minimalną stertę można zaimplementować przy użyciu klasy PriorityQueue z pliku System.Collections.Generic przestrzeń nazw . Klasa PriorityQueue to kolejka priorytetowa, która umożliwia przechowywanie elementów w strukturze danych przypominającej kolejkę, w której każdy element ma powiązany z nim priorytet.
Składnia:
C# var minHeap = new PriorityQueue ();>
5. Min-sterta w JavaScript
Min sterta to drzewo binarne, w którym każdy węzeł ma wartość mniejszą lub równą swoim dzieciom. W JavaScript możesz zaimplementować minimalną stertę za pomocą tablicy, gdzie pierwszy element reprezentuje węzeł główny, a dzieci węzła o indeksie I znajdują się na indeksach 2i+1 I 2i+2.
Składnia:
JavaScript const minHeap = new MinHeap();>
Różnica między stertą minimalną a stertą maksymalną:
|
| Min. sterta | Maksymalna sterta |
|---|---|---|
| 1. | W Min-Heap klucz obecny w węźle głównym musi być mniejszy lub równy spośród kluczy obecnych u wszystkich jego dzieci. | W Max-Heap klucz obecny w węźle głównym musi być większy lub równy spośród kluczy obecnych u wszystkich jego dzieci. |
| 2. | W Min-Heap minimalny element klucza znajduje się w katalogu głównym. | W Max-Heap maksymalny element klucza znajduje się w katalogu głównym. |
| 3. | Min-Heap używa rosnącego priorytetu. | Max-Heap używa malejącego priorytetu. |
| 4. | W konstrukcji Min-Heap priorytet ma najmniejszy element. | W konstrukcji Max-Heap priorytet ma największy element. |
| 5. | W Min-Heap najmniejszy element jest pierwszym, który zostanie wyrzucony ze sterty. | W Max-Heap największy element jest pierwszym, który zostanie wyrzucony ze sterty. |
Wewnętrzna implementacja struktury danych Min-Heap:
A Minimalna sterta jest zwykle reprezentowana jako tablica .
- Element główny będzie w Arr[0] .
- Dla dowolnego i-węzła Arr[i] :
- Arr[(i -1) / 2] zwraca swój węzeł nadrzędny.
- Arr[(2 * i) + 1] zwraca lewy węzeł podrzędny.
- Arr[(2 * i) + 2] zwraca prawy węzeł podrzędny.
Wewnętrzna implementacja Min-Heap wymaga 3 głównych kroków:
- Wprowadzenie : Aby wstawić element do sterty min, najpierw dołączamy element na końcu tablicy, a następnie dostosowujemy właściwość sterty, wielokrotnie zamieniając element z jego rodzicem, aż znajdzie się we właściwej pozycji.
- Usunięcie : Aby usunąć minimalny element ze sterty min, najpierw zamieniamy węzeł główny z ostatnim elementem tablicy, usuwamy ostatni element, a następnie dostosowujemy właściwość sterty, wielokrotnie zamieniając element z jego najmniejszym dzieckiem, aż znajdzie się w prawidłowa pozycja.
- Zgromadź : Operacji heapify można użyć do utworzenia minimalnej sterty z nieposortowanej tablicy.
Operacje na strukturze danych min-heap i ich implementacja:
Oto kilka typowych operacji, które można wykonać na strukturze danych sterty:
1. Wstawienie do struktury danych Min-Heap :
Elementy można wstawiać do sterty, stosując podobne podejście, jak omówiono powyżej w celu usunięcia. Pomysł jest taki:
Zamień ciąg JavaScript
- Operacja wstawiania na stercie min obejmuje następujące kroki:
- Dodaj nowy element na koniec sterty, na kolejnej dostępnej pozycji na ostatnim poziomie drzewa.
- Porównaj nowy element z jego rodzicem. Jeśli element nadrzędny jest większy niż nowy element, zamień je.
- Powtarzaj krok 2, aż element nadrzędny będzie mniejszy lub równy nowemu elementowi lub dopóki nowy element nie osiągnie korzenia drzewa.
- Nowy element znajduje się teraz we właściwej pozycji na stercie min, a właściwość sterty jest spełniona.
Ilustracja:
Załóżmy, że sterta jest mini-stertą jako:
Wstawienie do Min-Heap
Implementacja operacji wstawiania w Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Dodaj nowy element na końcu sterty heap.push_back(value); // Pobiera indeks ostatniego elementu int indeks = heap.size() - 1; // Porównaj nowy element z jego rodzicem i // zamień, jeśli to konieczne, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Przejdź w górę drzewa do rodzica // bieżącego elementu indeks = (indeks - 1) / 2; } } // Główna funkcja do testowania funkcji wstaw_min_heap int main() { wektor sterta; int wartości [] = { 10, 7, 11, 5, 4, 13 }; int n = rozmiar(wartości) / rozmiar(wartości[0]); for (int i = 0; tj< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Jawa import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && sterta[(indeks - 1) / 2]> sterta[indeks]) { swap(sterta, indeks, (indeks - 1) / 2); // Przejdź w górę drzewa do rodzica // bieżącego elementu indeks = (indeks - 1) / 2; } } // Funkcja zamieniająca dwa elementy w tablicy public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temperatura; } // Główna funkcja do testowania funkcji wstawMinHeap public static void main(String[] args) { int[] heap = new int[6]; int[] wartości = { 10, 7, 11, 5, 4, 13 }; int rozmiar = 0; for (int i = 0; tj< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 i sterta[(indeks - 1) // 2]> sterta[indeks]: sterta[indeks], sterta[(indeks - 1) // 2] = sterta[(indeks - 1) // 2], sterta[ indeks] # Przesuń w górę drzewa do rodzica bieżącego elementu indeks = (indeks - 1) // 2 sterty = [] wartości = [10, 7, 11, 5, 4, 13] dla wartości w wartościach: wstaw_min_heap( sterta, wartość) print(f'Wstawiono {wartość} do minimalnej sterty: {sterta}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List sterta, int wartość) { // Dodaj nowy element na końcu sterty sterty.Add(wartość); // Pobieranie indeksu ostatniego elementu int indeks = heap.Count - 1; // Porównaj nowy element z jego rodzicem i zamień // jeśli to konieczne while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; sterta[indeks] = sterta[(indeks - 1) / 2]; sterta[(indeks - 1) / 2] = temperatura; // Przejdź w górę drzewa do rodzica // bieżącego elementu indeks = (indeks - 1) / 2; } } // Główna funkcja do testowania funkcji InsertMinHeap public static void Main() { List sterta = nowa lista (); int[] wartości = { 10, 7, 11, 5, 4, 13 }; foreach(int wartość w wartościach) { InsertMinHeap(sterta, wartość); Console.Write('Wstawiono ' + wartość + ' do minimalnej sterty: '); foreach(int element na stercie) { Console.Write(element + ' '); } Konsola.WriteLine(); } } }> JavaScript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && sterta[parentIndex]> sterta[indeks]) { [sterta[indeks], sterta[parentIndeks]] = [sterta[parentIndeks], sterta[indeks]]; indeks = indeks nadrzędny; parentIndex = Math.floor((indeks - 1) / 2); } } // Przykład użycia const heap = []; wartości stałe = [10, 7, 11, 5, 4, 13]; for (stała wartość wartości) { wstawMinHeap(sterta, wartość); console.log(`Wstawiono ${value} do minimalnej sterty: ${heap}`); }> Wyjście
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Złożoność czasowa: O(log(n)) ( gdzie n jest liczbą elementów na stercie )
Przestrzeń pomocnicza: NA)
2. Usunięcie struktury danych Min-Heap :
Usuwanie najmniejszego elementu (korzenia) ze sterty min. Korzeń jest zastępowany ostatnim elementem sterty, a następnie przywracana jest właściwość sterty poprzez zamianę nowego korzenia z jego najmniejszym dzieckiem, aż rodzic będzie mniejszy od obu dzieci lub dopóki nowy korzeń nie osiągnie węzła liścia.
- Zastąp korzeń lub element do usunięcia ostatnim elementem.
- Usuń ostatni element ze sterty.
- Ponieważ ostatni element jest teraz umieszczony w pozycji węzła głównego. Może więc nie być zgodny z właściwością sterty. Dlatego złóż ostatni węzeł umieszczony w miejscu korzenia.
Ilustracja :
Załóżmy, że sterta jest mini-stertą jako:
Struktura danych minimalnej sterty
Elementem do usunięcia jest root, czyli 13.
Proces :
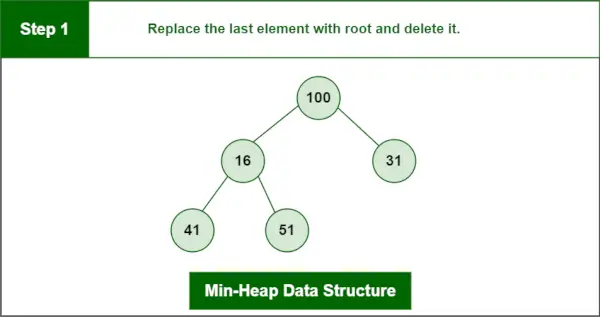
Ostatni element to 100.
Krok 1: Zamień ostatni element na root i usuń go.
Struktura danych minimalnej sterty
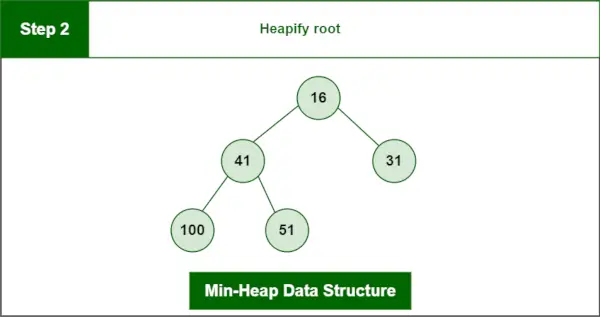
Krok 2 : Obsyp korzeń.
Ostatnia sterta:
Struktura danych minimalnej sterty
Implementacja operacji usuwania w Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Dodaj nowy element na końcu sterty heap.push_back(value); // Pobiera indeks ostatniego elementu int indeks = heap.size() - 1; // Porównaj nowy element z jego rodzicem i zamień, // jeśli to konieczne while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Przejdź w górę drzewa do rodzica // bieżącego elementu indeks = (indeks - 1) / 2; } } // Funkcja usuwająca węzeł ze sterty min void Delete_min_heap(vector & heap, int wartość) { // Znajdź indeks elementu do usunięcia int indeks = -1; for (int i = 0; tj< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector sterta; int wartości [] = { 13, 16, 31, 41, 51, 100 }; int n = rozmiar(wartości) / rozmiar(wartości[0]); for (int i = 0; tj< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Jawa import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List sterta, int wartość) { // Dodaj nowy element na końcu sterty heap.add(value); // Pobiera indeks ostatniego elementu int indeks = heap.size() - 1; // Porównaj nowy element z jego rodzicem i zamień // jeśli to konieczne while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, indeks, (indeks - 1) / 2); // Przejdź w górę drzewa do rodzica // bieżącego elementu indeks = (indeks - 1) / 2; } } // Funkcja usuwająca węzeł z publicznej statycznej sterty min. void usuńMinHeap(List sterta, int wartość) { // Znajdź indeks elementu do usunięcia int indeks = -1; for (int i = 0; tj< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List sterta = nowa lista tablic (); int[] wartości = { 13, 16, 31, 41, 51, 100 }; int n = wartości.długość; for (int i = 0; tj< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 i sterta[(indeks - 1) // 2]> sterta[indeks]: sterta[indeks], sterta[(indeks - 1) // 2] = sterta[(indeks - 1) // 2], sterta[ indeks] indeks = (indeks - 1) // 2 def usuń_min_heap(sterta, wartość): indeks = -1 dla i w zakresie(len(sterta)): if sterta[i] == wartość: indeks = łamię jeśli indeks == -1: zwróć stertę[indeks] = stertę[-1] stertę.pop() while True: lewe_dziecko = 2 * indeks + 1 prawe_dziecko = 2 * indeks + 2 najmniejsze = indeks, jeśli lewe_dziecko< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List sterta = nowa lista (); public void Wstaw (wartość int) { sterta.Dodaj (wartość); int indeks = sterta.Count - 1; while (indeks> 0 && sterta[(indeks - 1) / 2]> sterta[indeks]) { Zamień(indeks, (indeks - 1) / 2); indeks = (indeks - 1) / 2; } } public void Delete(int wartość) { int indeks = sterta.IndexOf(wartość); if (indeks == -1) { powrót; } sterta[indeks] = sterta[sterta.Ilość - 1]; sterta.UsuńAt(sterta.Count - 1); while (true) { int leftChild = 2 * indeks + 1; int praweDziecko = 2 * indeks + 2; int najmniejszy = indeks; if (leftChild< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> JavaScript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && sterta[flr]> sterta[indeks]; flr = Math.floor((indeks - 1) / 2)) { [sterta[indeks], sterta[flr]] = [ sterta[flr], sterta[indeks], ]; // Przejdź w górę drzewa do rodzica bieżącego elementu indeks = Math.floor((indeks - 1) / 2); } } funkcja usuwaniaMinHeap(heap, wartość) { // Znajdź indeks elementu do usunięcia niech indeks = -1; dla (niech i = 0; tj< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Wyjście
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Złożoność czasowa : O(log n) gdzie n oznacza liczbę elementów na stercie
Przestrzeń pomocnicza: NA)
3. Operacja podglądu na strukturze danych Min-Heap:
Aby uzyskać dostęp do minimalnego elementu (tj. korzenia sterty), zwracana jest wartość węzła głównego. Złożoność czasowa zaglądania do min-sterty wynosi O(1).
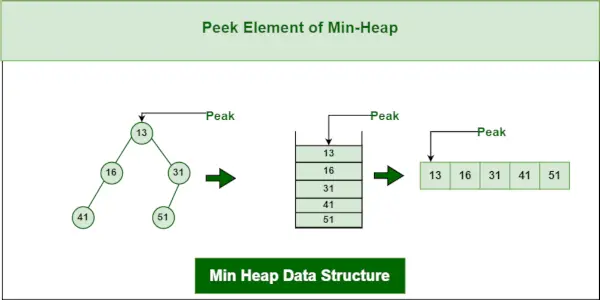
Struktura danych minimalnej sterty
Implementacja operacji Peek w Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , większy > minSterta; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Pobierz element szczytowy (tj. największy element) intpeakElement = minHeap.top(); // Wydrukuj element szczytowy cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Jawa import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = nowa kolejka priorytetów(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Pobieranie elementu szczytowego (tzn. największego) intpeakElement = minHeap.peek(); // Wydrukuj element szczytowy System.out.println('Element szczytowy: ' +peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Pobierz element szczytowy (tj. najmniejszy element) intpeakElement = minHeap.Peek(); // Wydrukuj element szczytowy Console.WriteLine('Element szczytowy: ' +peakElement); } }> JavaScript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Pobieranie elementu szczytowego (tj. najmniejszego elementu) constpeakElement = minHeap.peek(); // Wydrukuj element szczytowy console.log(`Element szczytowy: ${peakElement}`);> Wyjście
Peak element: 1>
Złożoność czasowa : W minimalnej stercie zaimplementowanej przy użyciu tablicy lub listy dostęp do elementu szczytowego można uzyskać w stałym czasie, O(1), ponieważ zawsze znajduje się on w korzeniu sterty.
W stercie minimalnej zaimplementowanej przy użyciu drzewa binarnego dostęp do elementu szczytowego można również uzyskać w czasie O(1), ponieważ zawsze znajduje się on w korzeniu drzewa.
Przestrzeń pomocnicza: NA)
4. Operacja Heapify na strukturze danych Min-Heap:
Operacji heapify można użyć do utworzenia minimalnej sterty z nieposortowanej tablicy. Odbywa się to poprzez rozpoczęcie od ostatniego węzła innego niż liść i wielokrotne wykonywanie operacji bąbelkowania, aż wszystkie węzły spełnią właściwość sterty.
Operacja Heapify w Min Heap
Implementacja operacji Heapify w Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int najmniejszy = i; int l = 2*i + 1; int r = 2*i + 2; jeśli (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector tablica = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Jawa // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Załóżmy, że pierwiastkiem jest początkowo najmniejszy element int najmniejszy = i; // Oblicz indeksy lewego i prawego dziecka bieżącego węzła int l = 2 * i + 1; int r = 2 * i + 2; // Porównaj lewe dziecko z obecnym najmniejszym if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Oryginalna tablica: '); // Wydrukuj oryginalną tablicę dla (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Sterta po operacji kopiowania: '); // Wydrukuj minimalną stertę po operacji sterty dla (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Pyton def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int najmniejszy = i; int po lewej = 2 * i + 1; int prawo = 2 * i + 2; // Porównaj lewe dziecko z bieżącym najmniejszym węzłem. jeśli (po lewej< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nowa lista {10, 5, 15, 2, 20, 30 }; Console.Write('Oryginalna tablica: '); foreach (int num w tablicy) Console.Write(num + ' '); // Wykonaj operację sterty na stercie min. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap po operacji stertowania: '); foreach (int num w tablicy) Console.Write(num + ' '); } }> JavaScript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Wydrukuj minimalną stertę po operacji stertowania console.log('Min-stertę po operacji stertowania: ' + arr.join(' ')); } // Wywołaj funkcję main, aby rozpocząć proces main();> Wyjście
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
Złożoność czasowa sterty w min-stercie wynosi O(n).
5. Operacja wyszukiwania w strukturze danych Min-Heap:
Aby wyszukać element na stercie min, można przeprowadzić wyszukiwanie liniowe w tablicy reprezentującej stertę. Jednakże złożoność czasowa przeszukiwania liniowego wynosi O(n), co nie jest efektywne. Dlatego wyszukiwanie nie jest powszechnie stosowaną operacją na stercie min.
Oto przykładowy kod pokazujący, jak szukać elementu na stercie minimalnej za pomocą std::znajdź() :
C++ #include using namespace std; int main() { priority_queue , większy > min_heap; // przykład maksymalnej sterty min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int element = 6; // znaleziony element bool = false; // Skopiuj stertę min do kolejki tymczasowej i wyszukaj // element std::priority_queue , większy > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { znaleziony = prawda; przerwa; } temp.pop(); } if (znaleziono) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Jawa import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = nowa kolejka priorytetów(); min_heap.add(3); // wstaw elementy do kolejki priorytetowej min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int element = 6; // znaleziono element do wyszukiwania wartości logicznej = false; // Skopiuj stertę min do kolejki tymczasowej i // wyszukaj element PriorityQueue temp = nowa kolejka priorytetów (min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { znaleziono = true; przerwa; } } if (found) { System.out.println( 'Znaleziono element na stercie min.'); } else { System.out.println( 'Nie znaleziono elementu na stercie min.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // przykład minimalnej sterty minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Kolejka(10); int element = 6; // znaleziony element bool = false; // Skopiuj stertę min do kolejki tymczasowej i wyszukaj // element var temp = new PriorityQueue (minSterta); while (temp.Count> 0) { if (temp.Peek() == element) { znaleziono = prawda; przerwa; } temp. Usuń z kolejki(); } if (found) { Console.WriteLine( 'Znaleziono element na stercie min.'); } else { Console.WriteLine( 'Nie znaleziono elementu na stercie min.'); } } }> JavaScript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { znaleziono = prawda; przerwa; } temp.dequeue(); } if (found) { console.log('Znaleziono element na stercie min.'); } else { console.log('Nie znaleziono elementu na stercie min.'); }> Wyjście
Element found in the min heap.>
Analiza złożoności :
The złożoność czasu tego programu jest O(n log n) , Gdzie N to liczba elementów w kolejce priorytetowej.
Operacja wstawiania ma złożoność czasową wynoszącą O(log n) w najgorszym przypadku, ponieważ należy zachować właściwość sterty. Operacja wyszukiwania polega na skopiowaniu kolejki priorytetowej do kolejki tymczasowej, a następnie przejściu przez kolejkę tymczasową, co zajmuje O(n log n) w najgorszym przypadku czas, ponieważ każdy element należy skopiować i usunąć z kolejki, a kolejka priorytetowa musi zostać przebudowana dla każdej operacji.
The złożoność przestrzeni programu jest NA) ponieważ przechowuje N elementy w kolejce priorytetowej i tworzy kolejkę tymczasową N elementy.
Zastosowania struktury danych Min-Heap:
- Sortowanie sterty: Minimalna sterta jest kluczowym elementem algorytmu sortowania sterty, który jest wydajnym algorytmem sortowania o złożoności czasowej O(nlogn).
- Kolejka priorytetowa: Kolejkę priorytetową można zaimplementować przy użyciu struktury danych o minimalnej stercie, w której element o minimalnej wartości zawsze znajduje się w katalogu głównym.
- Algorytm Dijkstry: W algorytmie Dijkstry minimalna sterta służy do przechowywania wierzchołków grafu w minimalnej odległości od wierzchołka początkowego. Wierzchołek z minimalną odległością znajduje się zawsze u podstawy sterty.
- Kodowanie Huffmana: W kodowaniu Huffmana sterta min służy do implementacji kolejki priorytetowej w celu zbudowania optymalnego kodu prefiksu dla danego zestawu znaków.
- Scal K posortowanych tablic: Mając K posortowanych tablic, możemy efektywnie połączyć je w jedną posortowaną tablicę, używając struktury danych o minimalnej stercie.
Zalety struktury danych min-heap:
- Efektywne wstawianie i usuwanie : Min sterta umożliwia szybkie wstawianie i usuwanie elementów o złożoności czasowej O(log n), gdzie n jest liczbą elementów na stercie.
- Efektywne pobieranie minimalnego elementu: Minimalny element sterty min znajduje się zawsze w korzeniu sterty, który można pobrać w czasie O(1).
- Oszczędność miejsca: Min sterta to zwarta struktura danych, którą można zaimplementować przy użyciu tablicy lub drzewa binarnego, co pozwala zaoszczędzić miejsce.
- Sortowanie: Min sterty można wykorzystać do zaimplementowania wydajnego algorytmu sortowania, takiego jak sortowanie na stercie ze złożonością czasową O(n log n).
- Kolejka priorytetowa: Minimalną stertę można wykorzystać do zaimplementowania kolejki priorytetowej, w której element o minimalnym priorytecie można efektywnie pobrać w czasie O(1).
- Wszechstronność: Min sterta ma kilka zastosowań w informatyce, w tym algorytmy wykresów, kompresję danych i systemy baz danych.
Ogólnie rzecz biorąc, sterta min jest użyteczną i wszechstronną strukturą danych, która oferuje wydajne operacje, oszczędność miejsca i ma kilka zastosowań w informatyce.