Regresja logistyczna w programowaniu R to algorytm klasyfikacji używany do wyznaczania prawdopodobieństwa powodzenia i niepowodzenia zdarzenia. Regresję logistyczną stosuje się, gdy zmienna zależna ma charakter binarny (0/1, prawda/fałsz, tak/nie). Funkcja logit jest używana jako funkcja łączenia w rozkładzie dwumianowym.
Prawdopodobieństwo binarnej zmiennej wynikowej można przewidzieć za pomocą techniki modelowania statystycznego znanej jako regresja logistyczna. Jest szeroko stosowany w wielu różnych branżach, w tym w marketingu, finansach, naukach społecznych i badaniach medycznych.
Funkcja logistyczna, powszechnie nazywana funkcją sigmoidalną, jest podstawową ideą leżącą u podstaw regresji logistycznej. Ta funkcja sigmoidalna jest używana w regresji logistycznej do opisania korelacji między zmiennymi predykcyjnymi a prawdopodobieństwem wyniku binarnego.

Regresja logistyczna w programowaniu w języku R
Regresja logistyczna jest również nazywana regresją Dwumianowa regresja logistyczna . Opiera się na funkcji sigmoidalnej, której wynikiem jest prawdopodobieństwo, a dane wejściowe mogą mieć wartość od -nieskończoności do + nieskończoności.
Teoria
Regresja logistyczna jest również znana jako uogólniony model liniowy. Ponieważ jest to technika klasyfikacji służąca do przewidywania odpowiedzi jakościowej, wartość y mieści się w zakresie od 0 do 1 i można ją przedstawić za pomocą następującego równania:

Regresja logistyczna w programowaniu w języku R
P jest prawdopodobieństwem interesującej cechy. Iloraz szans definiuje się jako prawdopodobieństwo sukcesu w porównaniu z prawdopodobieństwem porażki. Jest to kluczowa reprezentacja współczynników regresji logistycznej i może przyjmować wartości od 0 do nieskończoności. Iloraz szans równy 1 występuje wtedy, gdy prawdopodobieństwo sukcesu jest równe prawdopodobieństwu porażki. Iloraz szans równy 2 występuje wtedy, gdy prawdopodobieństwo sukcesu jest dwukrotnie większe niż prawdopodobieństwo porażki. Iloraz szans wynoszący 0,5 występuje wtedy, gdy prawdopodobieństwo niepowodzenia jest dwukrotnie większe niż prawdopodobieństwo sukcesu.
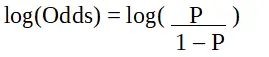
Regresja logistyczna w programowaniu w języku R
Ponieważ pracujemy z rozkładem dwumianowym (zmienną zależną), musimy wybrać funkcję łączenia, która najlepiej pasuje do tego rozkładu.
negacja dyskretna matematyka
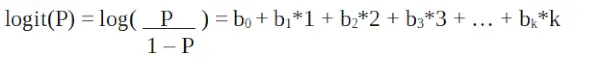
Regresja logistyczna w programowaniu w języku R
To jest funkcja logitowa . W powyższym równaniu nawiasy wybrano tak, aby zmaksymalizować prawdopodobieństwo zaobserwowania wartości próbek, a nie minimalizować sumę kwadratów błędów (jak zwykła regresja). Logit jest również znany jako dziennik szans. Funkcja logit musi być liniowo powiązana ze zmiennymi niezależnymi. To wynika z równania A, gdzie lewa strona jest liniową kombinacją x. Jest to podobne do założenia OLS, że y jest liniowo powiązane z x. Zmienne b0, b1, b2… itd. są nieznane i należy je oszacować na podstawie dostępnych danych uczących. W modelu regresji logistycznej pomnożenie b1 przez jedną jednostkę zmienia logit przez b0. Zmiany P spowodowane zmianą o jedną jednostkę będą zależeć od pomnożonej wartości. Jeśli b1 jest dodatnie, wówczas P wzrośnie, a jeśli b1 jest ujemne, wówczas P spadnie.
Zbiór danych
mtcars (test drogowy samochodu trendowego) obejmuje zużycie paliwa, osiągi i 10 aspektów projektowania samochodów dla 32 samochodów. Jest fabrycznie zainstalowany dplyr paczka w R.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
Hrithik Roshan
>
Wykonywanie regresji logistycznej na zbiorze danych
Regresja logistyczna jest implementowana w R przy użyciu glm() poprzez uczenie modelu przy użyciu funkcji lub zmiennych w zestawie danych.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Dzielenie danych
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Wyjście:
zablokowane numery
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Przechwytywanie) 1,58781 2,60087 0,610 0,5415 wt 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598 . --- Znaczenie. kody: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Parametr dyspersji dla rodziny dwumianowej przyjęty jako 1) Odchylenie zerowe: 34,617 na 24 stopniach swobody Odchylenie resztkowe: 20,212 na 22 stopnie swobody AIC: 26,212 Liczba iteracji Fishera Scoring: 6>
- Wywołanie: Wyświetlane jest wywołanie funkcji użyte do dopasowania modelu regresji logistycznej wraz z informacjami o rodzinie, formule i danych. Reszty odchylenia: Są to reszty odchylenia, które mierzą stopień dopasowania modelu. Oznaczają rozbieżności pomiędzy rzeczywistymi odpowiedziami a prawdopodobieństwem przewidywanym przez model regresji logistycznej. Współczynniki: te współczynniki w regresji logistycznej reprezentują logarytm szansy lub logit zmiennej odpowiedzi. Błędy standardowe związane z oszacowanymi współczynnikami przedstawiono w tabeli Std. Kolumna błędu. Kody istotności: Poziom istotności każdej zmiennej predykcyjnej jest wskazywany przez kody istotności. Parametr dyspersji: W regresji logistycznej parametr dyspersji służy jako parametr skalujący dla rozkładu dwumianowego. W tym przypadku jest ustawiona na 1, co wskazuje, że założone rozproszenie wynosi 1. Odchylenie zerowe: Odchylenie zerowe oblicza odchylenie modelu, gdy uwzględniony zostanie tylko wyraz wolny. Symbolizuje odchylenie, jakie wynikałoby z modelu bez predyktorów. Odchylenie resztkowe: Odchylenie resztkowe oblicza odchylenie modelu po dopasowaniu predyktorów. Oznacza odchylenie rezydualne po uwzględnieniu predyktorów. AIC: Kryterium informacyjne Akaike (AIC), które uwzględnia liczbę predyktorów, jest miernikiem dobroci dopasowania modelu. Karze bardziej skomplikowane modele, aby zapobiec nadmiernemu dopasowaniu. Modele lepiej dopasowane są wskazywane przez niższe wartości AIC. Liczba iteracji punktacji Fishera: Liczba iteracji wymaganych przez procedurę punktacji Fishera do oszacowania parametrów modelu jest wskazywana przez liczbę iteracji.
Przewiduj dane testowe na podstawie modelu
R
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Wyjście:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Wyjście:
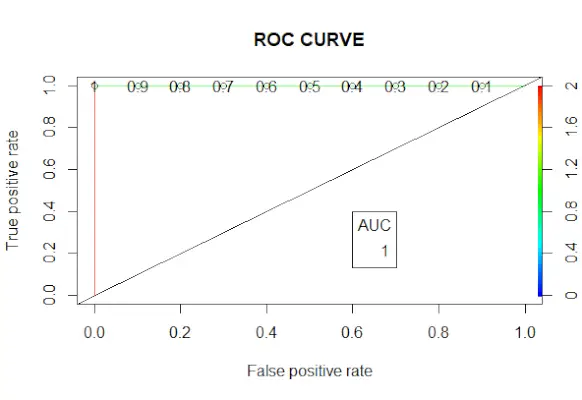
Krzywa ROC
Przykład 2:
Możemy wykonać model regresji logistycznej Titanic Data zestaw w R.
R
pomysł inteligentny kontra zaćmienie
Java lokalna data i czas
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Wyjście:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Przechwytywanie) 4.022e-16 8.660e-01 0 1 Klasa 2 -9.762e-16 1.000e+00 0 1 Klasa 3 -4.699e-16 1.000e+00 0 1 Klasa Załoga -5.551e-16 1.000e+ 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Parametr dyspersji dla rodziny dwumianowej przyjęty jako 1) Odchylenie zerowe: 44,361 na 31 stopniach swobody Odchylenie resztkowe: 44,361 na 26 stopniach swobody AIC: 56,361 Liczba iteracji Fishera Scoring: 2>
Narysuj krzywą ROC dla zbioru danych Titanica
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Wyjście:
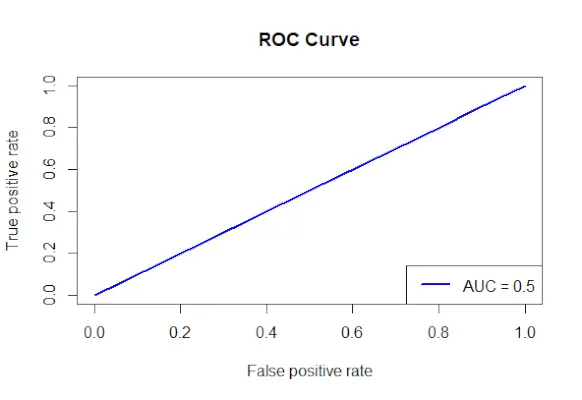
Krzywa ROC
- Określono czynniki stosowane do przewidywania przeżycia, a formuła Klasa przeżycia + płeć + wiek została wykorzystana do stworzenia modelu regresji logistycznej.
- Funkcja przewidywania() umożliwia przewidywanie zbioru danych przy użyciu dopasowanego modelu.
- Przewidywane prawdopodobieństwa są łączone z rzeczywistymi wartościami wyników w celu zbudowania obiektu przewidywania przy użyciu metody przewidywania() z pakietu ROCR.
- Określana jest miara prawdziwie dodatniego współczynnika (tpr) i miara fałszywie dodatniego współczynnika (fpr) na osi x, a następnie tworzony jest obiekt krzywej ROC przy użyciu funkcji performance() z pakietu ROCR.
- Obiekt krzywej ROC (roc_obj), który określa główny tytuł, kolor i szerokość linii, jest wykreślany za pomocą funkcji plot().
- Używa funkcji performance() z miarką = auc w celu określenia wartości AUC (obszaru pod krzywą) i dodaje do wykresu etykiety i legendę.
