Siłę normalną definiuje się jako siłę wywieraną przez dowolną powierzchnię na inny obiekt. Gdy ciało znajduje się w spoczynku, wypadkowa siła działająca na niego jest równa zeru. Siły normalnej nie można przyłożyć do dwóch powierzchni, które nie są ze sobą połączone. Można go interpretować jako składową siły skierowaną prostopadle do dowolnej powierzchni styku. Określa siłę, jaką ciało dostarcza do podłoża. Siła normalna jest równa ciężarowi obiektu tylko wtedy, gdy tempo zmiany prędkości obiektu jest ujemne, co oznacza, że ​​obiekt zwalnia.

Formuła

Wartość siły normalnej zależy od tego, gdzie przedmiot jest umieszczony względem drugiego obiektu. Kiedy obiekt spada, pozycja, w której obiekt spada na ziemię, określa wartość siły normalnej. Siła normalna jest oznaczona symbolem F_N. Jego jednostką miary są niutony (N), a wzór na wymiary podaje [M¹L¹T^-2]

Jeśli ciało spoczywa na płaskiej sile, siła normalna jest równa wartości ciężaru grawitacyjnego, czyli mg.

F _N = mg

Gdzie,

F_Njest siłą normalną,

m jest masą spoczywającego obiektu,

g jest przyspieszeniem ziemskim.

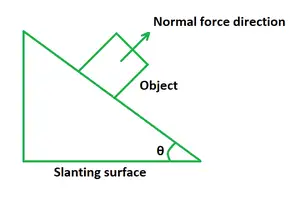
Jeśli ciało zsuwa się z pochyłej powierzchni pod pewnym kątem, wartością siły normalnej jest ciężar grawitacji dodany przez dodatkową siłę F sin θ. W tym przypadku siła normalna jest większa niż ciężar obiektu.

F _N = mg + F sin θ

Gdzie,

F_Njest siłą normalną,

m jest masą przesuwającego się obiektu,

g jest przyspieszeniem ziemskim,

θ jest kątem nachylenia.

Jeżeli siła działa na ciało w kierunku do góry, wartością siły normalnej jest ciężar grawitacyjny pomniejszony o siłę F sin θ. W tym przypadku siła normalna netto jest mniejsza niż ciężar obiektu.

F _N = mg – F sin θ

Gdzie,

„jaka” jest różnica między lwem a tygrysem

F_Njest siłą normalną,

m jest masą przesuwającego się obiektu,

g jest przyspieszeniem ziemskim,

θ jest kątem nachylenia.

Jeżeli ciało ułożone jest na pochyłej płaszczyźnie, siła normalna F_Njest równy iloczynowi ciężaru grawitacyjnego i cosinusa kąta nachylenia.

F _N = mg cos θ

Gdzie,

F_Njest siłą normalną,

m jest masą przesuwającego się obiektu,

g jest przyspieszeniem ziemskim,

θ jest kątem nachylenia.

Przykładowe problemy

Zadanie 1. Na stole leży przedmiot o masie 2 kg. Oblicz siłę normalną działającą na ten element.

Rozwiązanie:

Mamy,

m = 2

g = 9,8

Korzystając ze wzoru, który otrzymujemy,

F_N= mg

= 2 (9,8)

= 19,6 N

Zadanie 2. Obiekt spoczywa na stole pod działaniem siły 39,2 N. Oblicz działającą na niego siłę normalną.

Rozwiązanie:

Mamy,

F = 39,2

g = 9,8

Korzystając ze wzoru, który otrzymujemy,

F_N= mg

=> m = F/g

=> m = 39,2/9,8

=> m = 4 kg

Zadanie 3. Ciało o masie 10 kg zsuwa się z powierzchni nachylonej pod kątem 30° z siłą 200 N. Oblicz siłę normalną działającą na ten element.

Rozwiązanie:

Mamy,

F = 200

m = 10

nazwy miast usa

g = 9,8

θ = 30°

Korzystając ze wzoru, który otrzymujemy,

F_N= mg + F sin θ

= 10 (9,8) + 200 grzech 30°

= 98 + 200 (1/2)

= 98 + 100

= 198 N

Zadanie 4. Przedmiot o masie 20 kg zsuwa się z siły 400 N z pochyłej powierzchni pod kątem 30°. Oblicz siłę normalną działającą na ten element.

Rozwiązanie:

Mamy,

F = 400

m = 20

g = 9,8

θ = 30°

Korzystając ze wzoru, który otrzymujemy,

F_N= mg + F sin θ

= 20 (9,8) + 400 grzech 30°

= 196 + 400 (1/2)

= 196 + 200

= 396 N

Zadanie 5. Na skośnej powierzchni pod kątem 30° umieszczono przedmiot o masie 15 kg. Oblicz siłę normalną działającą na ten element, jeśli siła działająca w górę o wartości 100 N.

Rozwiązanie:

Mamy,

F = 100

m = 15

g = 9,8

θ = 30°

Korzystając ze wzoru, który otrzymujemy,

F_N= mg – F sin θ

= 15 (9,8) – 100 bez 30°

= 147 – 100 (1/2)

= 147 – 50

= 97 N

Zadanie 6. Na skośnej powierzchni pod kątem 60° umieszczono przedmiot o masie 5 kg. Oblicz siłę normalną działającą na ten element w dowolnym punkcie.

Rozwiązanie:

Mamy,

m = 5

g = 9,8

θ = 60°

Korzystając ze wzoru, który otrzymujemy,

F_N= mg cos θ

kolejność sql losowo

= 5 (9,8) (cos 60°)

= 49/2

= 24,5 N

Zadanie 7. Przedmiot umieszczono na skośnej powierzchni pod kątem 60°. Oblicz jego masę, jeżeli działająca na niego siła normalna wynosi 400 N.

Rozwiązanie:

Mamy,

F_N= 400,

θ = 60°

Korzystając ze wzoru, który otrzymujemy,

F_N= mg cos θ

m = F/(g cos θ)

= 400/ (9,8 × cos 60°)

= 400/4,9

= 81,63 N