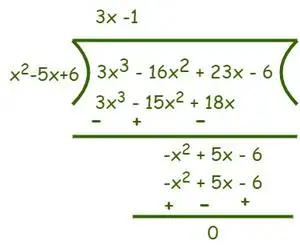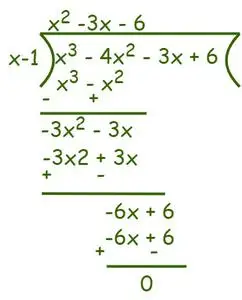Równanie sześcienne jest równaniem matematycznym, w którym wielomian stopnia 3 jest równa stałej lub innemu wielomianowi maksymalnego stopnia 2. Standardowa reprezentacja równania sześciennego to topór ³ +bx ² +cx+d = 0 gdzie a, b, c i d są liczbami rzeczywistymi. Oto kilka przykładów równań sześciennych X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 itp.

Spis treści

• Definicja wielomianu
• Stopień równania
• Definicja równania sześciennego
• Jak rozwiązywać równania sześcienne?
• Rozwiązywanie równań sześciennych
• Rozwiązywanie równań sześciennych za pomocą współczynników
• Rozwiązywanie równań sześciennych metodą graficzną
• Zadania oparte na rozwiązywaniu równań sześciennych
• Ćwicz problemy dotyczące rozwiązywania równań sześciennych

Aby dowiedzieć się, jak rozwiązywać równania sześcienne, musimy najpierw poznać wielomiany, stopień wielomianu i inne. W tym artykule dowiemy się szczegółowo o wielomianach, równaniach wielomianowych, rozwiązywaniu równań sześciennych lub o tym, jak rozwiązywać równania sześcienne i inne.

Definicja wielomianu

Wielomian definiuje się następująco:

A wielomian jest wyrażeniem algebraicznym, w którym potęga zmiennej jest nieujemną liczbą całkowitą. Ogólna postać wielomianu to a₀X^N+ za₁X^n-1+ za₂X^n-2+… + a_N. W zależności od maksymalnej mocy zmiennej wielomian można sklasyfikować jako jednomian, dwumian, trójmian i tak dalej.

Co to jest równanie?

Równanie definiuje się następująco:

Równanie to wielomian, który jest przyrównywany do wartości liczbowej lub dowolnego innego wielomianu. Na przykład x + 2 jest wielomianem, ale x + 2 = 5 jest równaniem. Podobnie 2x + 3 = x + 1 jest również równaniem, podczas gdy 2x + 3 i x + 1 są indywidualnie wielomianami.

Stopień równania

Definicja stopnia równania znajduje się poniżej:

Stopień równania definiuje się jako maksymalną moc posiadaną przez zmienną w równaniu.

Na podstawie stopnia równania równanie można sklasyfikować w następujący sposób:

• Równanie liniowe
• Równanie kwadratowe
• Równanie sześcienne
• Równanie dwukwadratowe

Równanie liniowe

Równanie, w którym maksymalna moc zmiennej wynosi 1, nazywa się równaniem liniowym.

• Na przykład 3x +1 = 0

Wielomian kwadratowy

Równanie, w którym maksymalna moc zmiennej wynosi 2, jest równaniem kwadratowym.

• Na przykład 3x²+x+1 = 0

Równanie sześcienne

Równanie, w którym maksymalna moc zmiennej wynosi 3, nazywa się równaniem sześciennym.

jaki jest system plików Linuxa

• Na przykład 5x³+3x²+x+1 = 0

Wielomian dwukwadratowy

Równanie, w którym maksymalna moc zmiennej wynosi 4, nazywa się wielomianem dwukwadratowym lub wielomianem kwarcowym.

• Na przykład 5x⁴+4x³+3x²+2x+1 = 0

Definicja równania sześciennego

Równanie sześcienne jest równaniem algebraicznym, w którym najwyższy stopień wielomianu wynosi 3. Niektóre przykłady równań sześciennych to 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 itd.

Ogólna postać równania sześciennego to:

topór ³ + bx ² + cx + d = 0, a ≠ 0

Gdzie,

• a, b, I C są współczynnikami zmiennej i ich wykładnikami i D jest stałą, oraz
• a, b, c I D są liczbami rzeczywistymi.

Jak rozwiązywać równania sześcienne?

Równanie sześcienne jest równaniem trzeciego stopnia. Ma trzy rozwiązania i można je łatwo rozwiązać, wykonując kroki dodane poniżej,

Krok 1: Znajdź jedno rozwiązanie równania sześciennego metodą „uderz i spróbuj”. Załóżmy, że mamy równanie sześcienne P(x), a następnie znajdź dowolne x = a, P(a) = 0, przyjmując, x = 0, ±1, ±2, ±3,… i tak.

Krok 2: Kiedy otrzymamy P(a) = 0, znajdź współczynnik (x – a) P(x)

Krok 3: Podziel P(x) przez (x – a), aby otrzymać równanie kwadratowe, powiedzmy Q(x), używając dzielenia wielomianowego.

Krok 4: Faktaryzuj równanie kwadratowe Q(x), aby uzyskać współczynniki jako (x – b) i (x – c).

Krok 5: (x – a), (x – b) i (x – c) są czynnikami P(x) i rozwiązując każdy czynnik otrzymujemy pierwiastki równań jako, a, b i c.

Dowiedz się więcej o, Dzielenie wielomianu

Rozwiązywanie równań sześciennych

A Równanie sześcienne można rozwiązać dwoma metodami

• Redukując to do równania kwadratowego, a następnie rozwiązując je za pomocą rozkładu na czynniki lub wzoru kwadratowego
• Metodą graficzną

A Równanie sześcienne ma trzy korzenie. Korzenie te mogą być rzeczywiste lub wyimaginowane. Mogą również istnieć różne korzenie lub dwa takie same i jeden inny korzeń i wszystkie trzy takie same korzenie.

Należy zauważyć, że dla dowolnego równania, w tym Równania sześcienne , przed rozwiązaniem równania należy zawsze najpierw ułożyć równanie w postaci standardowej.

Na przykład, jeśli dane równanie wynosi 2x²-5 = x + 4/x, to musimy to ponownie ułożyć w standardową postać, tj. 2x³-X²-5x-4 = 0. Teraz możemy rozwiązać równanie dowolną odpowiednią metodą.

Rozwiązywanie równań sześciennych za pomocą współczynników

Rozwiązanie równania sześciennego za pomocą twierdzenia o czynnikach wyjaśniono na przykładzie dodanym poniżej,

Przykład: Znajdź pierwiastki równania f(x) = 3x ³ −16x ² + 23x - 6 = 0.

Rozwiązanie:

Dane wyrażenie: f(x) = 3x³−16x²+ 23x - 6 = 0

Najpierw rozłóż wielomian na czynniki, aby uzyskać pierwiastki

Ponieważ stała wynosi -6, możliwymi współczynnikami są 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Wiemy to wg Twierdzenie o czynnikach jeśli f(a) = 0, to (x-a) jest współczynnikiem f(x)

Zatem (x – 2) i (x – 3) są czynnikami f(x). Dlatego iloczyn (x – 2) i (x – 3) będzie również współczynnikiem f(x). Teraz, aby znaleźć pozostałe czynniki, użyj metody długiego dzielenia i podziel f(x) przez iloczyn (x – 2) i (x – 3)

Zatem Dzielnik = (x – 2)(x – 3) = (x²– 5x + 6) i Dywidenda = 3x³−16x²+ 23x − 6. Teraz podziel jak pokazano poniżej,

Po podzieleniu otrzymujemy (3x-1) jako iloraz, a reszta wynosi 0. Teraz zgodnie z Algorytm dzielenia wiemy to Dywidenda = Dzielnik×Iloraz+Reszta.

⇒ f(x) = (3x³−16x²+ 23x - 6) = (x²– 5x + 6)(3x-1)

Ponieważ f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 lub 3x-1 = 0

Teraz weźmiemy 3x-1 = 0 ⇒ x = 1/3, ponieważ znamy już dwa pierwiastki z x²– 5x + 6, czyli 2 i 3

Więc,

Korzenie danego Równanie sześcienne to 1/3, 2 i 3.

Rozwiązywanie równań sześciennych metodą graficzną

Równanie sześcienne rozwiązuje się graficznie, gdy nie można rozwiązać danego równania innymi technikami. Potrzebujemy więc dokładnego rysunku danego równania sześciennego. Pierwiastkami równania są punkty, w których wykres przecina oś X, jeśli równanie jest wyrażone w postaci x, a jeśli równanie jest wyrażone w postaci y, wówczas pierwiastkami równania są punkty, w których wykres przecina oś Y.

Liczba rzeczywistych rozwiązań równania sześciennego jest równa liczbie przecięć wykresu równania sześciennego przez oś X.

Przykład: Znajdź pierwiastki równania f(x) = x ³ − 4x ² − 9x + 36 = 0, stosując metodę graficzną.

Rozwiązanie:

Dane wyrażenie: f(x) = x³− 4x²− 9x + 36 = 0.

Teraz po prostu zamień losowe wartości na x na wykresie dla danej funkcji:

X	-4	-3	-2	-1	0	1	2	3	4	5
k(x)	-56	0	19	40	36	24	10 Java przerwała pętlę	0	0	16

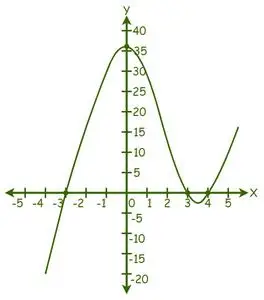
Widzimy, że wykres przeciął oś X w 3 punktach, zatem istnieją 3 rzeczywiste rozwiązania.

Z wykresu rozwiązaniami są: x = -3, x = 3 i x = 4.

Zatem pierwiastki danego równania to -3, 3 i 4.

Czytaj więcej,

• Równanie liniowe
• Rozwiązywanie równań kwadratowych
• Rozkładanie wielomianów na czynniki

Zadania oparte na rozwiązywaniu równań sześciennych

Zadanie 1: Znajdź pierwiastki f(x) = x ³ – 4x ² -3x + 6 = 0.

Rozwiązanie:

Dane wyrażenie: f(x) = x³– 4x²-3x + 6 = 0.

Najpierw rozłóż wielomian na czynniki, aby uzyskać pierwiastki.

Ponieważ stała wynosi +6, możliwe czynniki to 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Zatem według Twierdzenie o czynnikach (x – 1) jest współczynnikiem danego równania. Teraz, aby znaleźć pozostałe czynniki, użyj metody długiego dzielenia.

Według Algorytm dzielenia możemy pisać,

Zatem f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 lub (x²– 3x – 6) = 0

Wiemy, że pierwiastki równania kwadratowego topór²+ bx + c = 0 są,

x = [-b ± √(b²-4ac)]/2a

Zatem dla (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Zatem pierwiastki danego równania sześciennego wynoszą 1, (3+√33)/2 i (3–√33)/2.

Zadanie 2: Znajdź pierwiastki równania f(x) = 4x ³ – 10x ² + 4x = 0.

Rozwiązanie:

Dane wyrażenie: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

Sonu Nigam

⇒ x = 0 lub 4x – 2 = 0, x – 2 = 0

⇒ x = 0 lub x = 1/2 lub x = 2

Zatem pierwiastki danego równania to 0, 1/2 i 2.

Zadanie 3: Znajdź pierwiastki równania f(x) = x ³ + 3x ² + x + 3 = 0.

Rozwiązanie:

Dane wyrażenie: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 lub x²+1 = 0

⇒ x = -3, ±i

Zatem dane równanie ma pierwiastek rzeczywisty, tj. -3, i dwa pierwiastki urojone, tj. ±i.

Zadanie 4: Znajdź pierwiastki równania f(x) = x ³ – 7x ² – x + 7 = 0.

Rozwiązanie:

Biorąc pod uwagę wyrażenia,

f(x) = x³– 3x²– 5x + 7 = 0

Najpierw rozłóż równanie na czynniki, f(x): x³– 3x²– 5x + 7= 0

Można to rozłożyć na czynniki (x-7)(x+1)(x-1) = 0

Po rozłożeniu wielomianu na czynniki możemy znaleźć pierwiastki, przyrównując każdy czynnik do zera. Na przykład:

• x – 7 = 0, więc x = 7
• x + 1 = 0, więc x = -1
• x – 1 = 0, więc x = 1

Zatem pierwiastki równania f(x): x³– 3x²– 5x + 7 = 0 arów

• x = 7
• x = -1
• x = 1

Zadanie 5: Znajdź pierwiastki równania f(x) = x ³ − 6x ² + 11x − 6 = 0, stosując metodę graficzną.

Rozwiązanie:

Dane wyrażenie: f(x) = x³− 6x²+ 11x - 6 = 0.

Teraz po prostu zamień losowe wartości na x na wykresie dla danej funkcji:

X	1	2	3	4	5
k(x)	0	0	0	6	24 wiosna i wiosna mvc

Widzimy, że wykres przeciął oś X w 3 punktach, zatem istnieją 3 rzeczywiste rozwiązania.

Z wykresu rozwiązaniami są: x = 1, x = 2 i x = 3.

Zatem pierwiastkami danego równania są liczby 1, 2 i 3.

Ćwicz problemy dotyczące rozwiązywania równań sześciennych

Poniżej dodano różne problemy praktyczne związane z równaniami sześciennymi. Rozwiąż te problemy, aby w pełni zrozumieć koncepcję Jak rozwiązać równanie sześcienne?

P1. Rozwiąż równanie sześcienne, 3x³+ 2x²– 11x + 7 = 0.

P2. Znajdź pierwiastki równania sześciennego, 4x³– 12x²+ 17 = 0.

P3. Rozwiąż równanie sześcienne x³+ 4x²– x + 3 = 0 metodą graficzną.

P4. Znajdź liczbę, która spełnia wymagania, -9x³+ 11x²– 8x + 2 = 0.

Często zadawane pytania dotyczące rozwiązywania równań sześciennych

1. Czym są równania sześcienne?

Równania sześcienne to równania algebraiczne, w których maksymalna moc zmiennej wynosi 3

2. Jak uwzględnić równanie sześcienne?

Równanie sześcienne możemy rozłożyć na czynniki na dwa sposoby. Najpierw biorąc wyrażenie liniowe wspólne z danego równania sześciennego, wówczas otrzymamy wyrażenie liniowe i kwadratowe jako iloczyn. To równanie kwadratowe można dalej rozłożyć na czynniki, aby uzyskać wszystkie czynniki. Druga metoda polega na znalezieniu zera danego równania sześciennego poprzez wstawienie losowych wartości. Wartość, dla której otrzymamy wartość równania równą zero, będzie jednym z zer danego równania sześciennego. Teraz, korzystając z twierdzenia o czynnikach, utwórz wyrażenie liniowe, powiedzmy x-a i podziel dane równanie sześcienne przez to wyrażenie, co da równanie kwadratowe jako iloraz. Otrzymane równanie kwadratowe można dalej rozłożyć na czynniki, aby uzyskać wszystkie czynniki.

3. Jak graficznie rozwiązać równanie sześcienne?

Aby rozwiązać równanie sześcienne, graficznie umieść losowe wartości x w danym równaniu sześciennym i rozwiąż, otrzymasz wartości y. Uzyskane wartości nanieś na wykres. Znajdź współrzędne, w których wykres przecina oś x. Współrzędne te są rozwiązaniem równania sześciennego.

4. Czy wszystkie równania sześcienne można rozwiązać dokładnie?

Każde równanie o nieparzystej mocy musi mieć jeden pierwiastek rzeczywisty. Dlatego równanie sześcienne musi mieć co najmniej jeden pierwiastek rzeczywisty, w przeciwieństwie do równania kwadratowego, w którym oba pierwiastki mogą być urojone, gdy wyróżnik jest mniejszy od zera.

5. Czy równanie sześcienne może mieć wiele rozwiązań?

Tak, równania sześcienne mogą mieć wiele rozwiązań, ponieważ równanie sześcienne może mieć maksymalnie trzy różne pierwiastki rzeczywiste.

6. Co rozumiesz przez stopień równania?

Maksymalna moc, jaką posiada zmienna w równaniu, nazywana jest stopniem wielomianu.

7. Jaka jest różnica między wielomianem a równaniem?

Wielomian to po prostu równanie algebraiczne, w którym potęga zmiennej jest nieujemną liczbą całkowitą. Ten wielomian po zrównaniu (=) z wartością liczbową lub innym wielomianem nazywa się równaniem.

8. Co to jest twierdzenie o czynnikach dla równań sześciennych?

Twierdzenie o czynnikach stwierdza, że ​​jeśli r jest pierwiastkiem (rozwiązaniem) równania sześciennego ax³+ bx²+ cx + d = 0, wówczas x – r jest czynnikiem równania.

9. Co się stanie, jeśli nie uda mi się znaleźć dokładnych rozwiązań za pomocą wzorów?

Jeśli znalezienie dokładnych rozwiązań wydaje się niemożliwe, możemy zastosować metody numeryczne, np. metody iteracyjne (np. metodę Newtona), aby przybliżyć pierwiastki równania.

Dowiedz się więcej o Metoda Newtona Raphsona .