Pierwiastek kwadratowy z 3 to dodatnia liczba rzeczywista, która po pomnożeniu przez samą siebie daje liczbę 3. Pierwiastek kwadratowy z 3 jest liczbą niewymierną, ponieważ jest to niekończący się i niepowtarzający się ułamek dziesiętny. Pierwiastek kwadratowy z 3 jest oznaczany jako √3 lub 31/2. Ponieważ kwadrat 3 jest liczbą niewymierną, nigdy nie oblicza się jej dokładnej wartości dziesiętnej.
otwórz menu ustawień
Wartość pierwiastka kwadratowego z 3, √3 =1,732 (obcięta)
W tym artykule dowiemy się szczegółowo o pierwiastku kwadratowym z 3.
Spis treści
- Co to jest pierwiastek kwadratowy z 3?
- Wartość pierwiastkowa 3 w matematyce
- Czy pierwiastek kwadratowy z 3 jest racjonalny czy irracjonalny?
- Jak znaleźć pierwiastek kwadratowy z 3?
- Właściwości pierwiastka kwadratowego z liczby
- Tabela pierwiastków kwadratowych
Co to jest pierwiastek kwadratowy z 3?
Pierwiastek kwadratowy z liczby to liczba, która pomnożona przez siebie daje liczbę pierwotną.
Przykład: Pierwiastek kwadratowy z 16 wynosi 4, ponieważ 4×4 = 16, więc √16 = 4
Pierwiastek kwadratowy z 3 lub po prostu pierwiastek 3 to liczba niewymierna, która pomnożona przez samą siebie daje liczbę 3. Możemy podać przybliżoną wartość pierwiastka 3 jako:
- Forma dziesiętna: 1,732
- Forma wykładnicza: 31/2
- Forma radykalna: √3
Wartość pierwiastkowa 3 w matematyce
W matematyce znalezienie pierwiastka kwadratowego dowolnej liczby jest bardzo ważne, pierwiastek kwadratowy z idealnego kwadratu można łatwo obliczyć. W przypadku niedoskonałych kwadratów znalezienie pierwiastka kwadratowego jest trudne i zwykle oblicza się je metodą długiego dzielenia.
Pierwiastek z 3 wyraża się jako √3. Jest to liczba niewymierna, dlatego nigdy nie można obliczyć jej wartości dziesiętnej. Jest to reprezentowane w postaci radykalnej jako (3)½. Pierwiastek kwadratowy z 3 zaokrąglonych do 7 miejsc po przecinku to 1,7320508.
Pierwiastek kwadratowy z 3 = 1,7320508075688772…
Czy pierwiastek kwadratowy z 3 jest racjonalny czy irracjonalny?
Pierwiastek kwadratowy 3 jest niekończącym się i niepowtarzalnym ułamkiem dziesiętnym, a wszystkie niezakończone i niepowtarzające się ułamki dziesiętne mieszczą się w liczbie niewymiernej. Można więc bezpiecznie powiedzieć, że √3 jest an Liczba niewymierna .
json w przykładzie json
Dziesiętne rozwinięcie pierwiastka kwadratowego z 3 to:
√3 = 1,7320508075688772…
Ponieważ nie jest powtarzalny i niekończący się, możemy z pewnością powiedzieć, że √3 jest irracjonalne.
Jak znaleźć pierwiastek kwadratowy z 3?
Zawsze łatwiej jest obliczyć pierwiastek kwadratowy z doskonałych kwadratów, ale aby obliczyć pierwiastek kwadratowy z niedoskonałego kwadratu, musimy zastosować metodę długiego dzielenia.
Aby obliczyć pierwiastek kwadratowy z 3, musimy wykonać kroki podane poniżej:
ile milionów jest w miliardzie
Krok 1: Zapisz 3 jako 3,000000 (gdzie zera zawsze są zapisywane w postaci par), aby ułatwić dzielenie.
Krok 2: Teraz znajdź idealny kwadrat mniejszy niż 3, tj. 1, i podziel przez niego liczbę.
Krok 3: Teraz iloraz wynosi 1, a reszta wynosi 2. Umieścimy przecinek w ilorazie i zmniejszymy parę zer w celu dalszego dzielenia.
Krok 4: Teraz następna dywidenda wyniesie 200, dodaj następny dzielnik będzie 2X (iloraz 1 jest dodawany do poprzedniego dzielnika 1, a X jest na dziesiątym miejscu), tak że pomnożenie liczby 2X i X powinno być mniejsze niż 200. To da następna wartość 27 jako nowy dzielnik.
Krok 5: Teraz do ilorazu po przecinku dodaje się 7, więc wartość ilorazu wyniesie 1,7, a nowy dzielnik otrzymamy przez dodanie 7 do 27, a więc 34Y, gdzie Y jest na miejscu setnym. Korzystając z poprzednich kroków, możemy kontynuować i otrzymać pierwiastek kwadratowy z 3 z ilorazu.
wybierz z wielu tabel sql
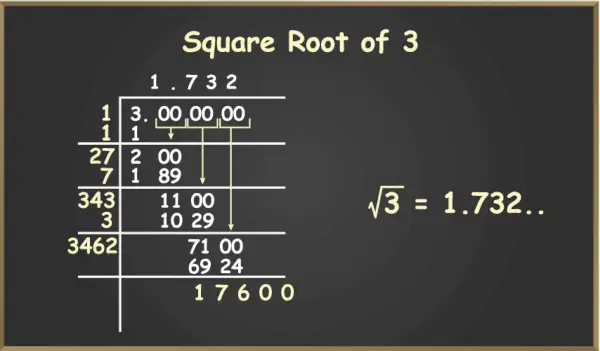
Pierwiastek kwadratowy z 3
Teraz zmniejsz następną parę zer i powtórz kroki 4 i 5. Można to zrobić dla nieskończonych kroków, ponieważ dokładna wartość pierwiastka kwadratowego z 2 sięga do nieskończonej liczby miejsc po przecinku. Wynik możemy obliczyć z dokładnością do 4 miejsc po przecinku, ponieważ można go wykorzystać dla ok. wartość pierwiastka kwadratowego.
Właściwości pierwiastka kwadratowego z liczby
Poniżej omówiono różne właściwości pierwiastka kwadratowego z liczby:
- Idealne liczby kwadratowe mają doskonałe pierwiastki kwadratowe.
- Pierwiastek kwadratowy z nawet idealnego kwadratu jest parzysty.
- Pierwiastek kwadratowy z nieparzystego doskonałego kwadratu jest nieparzysty.
- Pierwiastek kwadratowy liczby ujemnej to a Liczba zespolona .
Tabela pierwiastków kwadratowych
Pierwiastki kwadratowe różnych liczb są szeroko stosowane w matematyce. Poniższa tabela podaje pierwiastek kwadratowy różnych powszechnie używanych liczb.
| Numer | Pierwiastek kwadratowy |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1,414 (w przybliżeniu) |
| 3 | √(3) = 1,732 (w przybliżeniu) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2,236 (w przybliżeniu) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
Sprawdź także
- Pierwiastek kwadratowy z 2
- Liczby rzeczywiste
- Liczby wymierne
Często zadawane pytania dotyczące pierwiastka kwadratowego z 3
Jaka jest wartość pierwiastka kwadratowego z 3?
Przybliżona wartość pierwiastka kwadratowego z 3 wynosi 1,73205.
przekonwertuj obiekt Java na json
Dlaczego pierwiastek kwadratowy z 3 jest liczbą niewymierną?
Wartość pierwiastka kwadratowego z 3 jest niepowtarzającą się i niezakończoną liczbą dziesiętną, więc jest to liczba niewymierna.
Czy liczba 3 jest idealnym kwadratem?
3 jest liczbą pierwszą, a liczby pierwsze nie mają innych dzielników niż 1 i ona sama. Zatem możemy powiedzieć, że 3 nie jest idealnym kwadratem.
Jak znaleźć wartość √3?
Wartość √3 można znaleźć metodą długiego dzielenia. Ponieważ 3 nie jest idealnym kwadratem, dlatego nigdy nie można znaleźć jej dokładnej wartości.
Jaka jest wartość pierwiastka 2?
Pierwiastek 2 jest liczbą niewymierną, dlatego nigdy nie można znaleźć jej dokładnej wartości dziesiętnej. Przybliżona wartość pierwiastka 2 wynosi, √2 = 1,414 (w przybliżeniu)
