logo

TechCodeview

Silnie połączone komponenty

Silnie połączone komponenty (SCC) są podstawowym pojęciem w teorii grafów i algorytmach. W grafie skierowanym a Silnie połączony komponent jest podzbiorem wierzchołków, w którym do każdego wierzchołka w podzbiorze można dotrzeć z każdego innego wierzchołka w tym samym podzbiorze, przechodząc przez skierowane krawędzie. Znalezienie SCC wykresu może dostarczyć ważnych informacji na temat struktury i powiązań wykresu z zastosowaniami w różnych dziedzinach, takich jak analiza sieci społecznościowych, indeksowanie sieci i routing sieciowy . W tym samouczku omówione zostaną definicje, właściwości i wydajne algorytmy identyfikowania silnie połączonych komponentów w grafowych strukturach danych

jakie miesiące są q3

Spis treści



Co to są silnie powiązane komponenty (SCC)?

A silnie powiązany komponent grafu skierowanego to maksymalny podgraf, w którym każda para wierzchołków jest wzajemnie osiągalna. Oznacza to, że dla dowolnych dwóch węzłów A i B w tym podgrafie istnieje ścieżka z A do B i ścieżka z B do A.

Na przykład: Poniższy graf ma dwa silnie połączone komponenty {1,2,3,4} i {5,6,7}, ponieważ istnieje ścieżka z każdego wierzchołka do każdego innego wierzchołka w tym samym silnie połączonym komponencie.

scc_fianldrawio

Silnie połączony komponent



Dlaczego silnie połączone komponenty (SCC) są ważne?

Zrozumienie SCC ma kluczowe znaczenie dla różnych zastosowań, takich jak:

  • Analiza sieci : Identyfikacja skupisk ściśle połączonych węzłów.
  • Optymalizacja robotów sieciowych : Określanie części wykresu internetowego, które są ze sobą ściśle powiązane.
  • Rozwiązanie zależności : W oprogramowaniu zrozumienie, które moduły są współzależne.

Różnica między połączonymi i silnie połączonymi komponentami ( SCC)

Łączność w graf nieskierowany odnosi się do tego, czy dwa wierzchołki są osiągalne od siebie, czy nie. Mówi się, że dwa wierzchołki są połączone, jeśli istnieje między nimi ścieżka. Tymczasem Silnie połączone ma zastosowanie wyłącznie do wykresy skierowane . Za podgraf grafu skierowanego uważa się Silnie połączone komponenty (SCC) wtedy i tylko wtedy, gdy dla każdej pary wierzchołków A I B , istnieje ścieżka z A Do B i ścieżka z B Do A . Zobaczmy, dlaczego standardowa metoda dfs do wyszukiwania połączonych komponentów na wykresie nie można wykorzystać do określenia silnie powiązanych komponentów.

Rozważ następujący wykres:



scc_fianldrawio

Teraz zacznijmy dfs wywołaj z wierzchołka 1, aby odwiedzić inne wierzchołki.

dfs_finaldrawio

Dlaczego konwencjonalnej metody DFS nie można zastosować do znalezienia silnie połączonych komponentów?

Do wszystkich wierzchołków można dotrzeć z wierzchołka 1. Jednak wierzchołki 1 i 5,6,7 nie mogą znajdować się w tej samej silnie powiązanej składowej, ponieważ nie ma skierowanej ścieżki z wierzchołka 5,6 lub 7 do wierzchołka 1. Graf ma dwa silnie powiązane połączone komponenty {1,2,3,4} i {5,6,7}. Zatem do znalezienia silnie połączonych komponentów nie można zastosować konwencjonalnej metody dfs.

cykl życia SDLC

Łączenie dwóch silnie połączonych komponentów za pomocą jednokierunkowej krawędzi

Dwa różne połączone komponenty stają się pojedynczym komponentem, jeśli pomiędzy wierzchołkiem jednego komponentu a wierzchołkiem innego komponentu zostanie dodana krawędź. Nie dotyczy to jednak silnie połączonych komponentów. Dwa silnie połączone komponenty nie stają się jednym silnie połączonym komponentem, jeśli istnieje tylko jednokierunkowa krawędź pomiędzy jednym SCC a drugim SCC.

js ciąg wielowierszowy

unidrawio-(2)

Podejście brutalnej siły do ​​znajdowania silnie połączonych komponentów

Prosta metoda będzie polegać na tym, że dla każdego wierzchołka i (który nie jest częścią żadnego silnie połączonego komponentu) znajdziemy wierzchołki, które będą częścią silnie połączonego komponentu zawierającego wierzchołek i. Dwa wierzchołki i oraz j będą w tym samym silnie połączonym komponencie, jeśli istnieje skierowana ścieżka od wierzchołka i do wierzchołka j i odwrotnie.

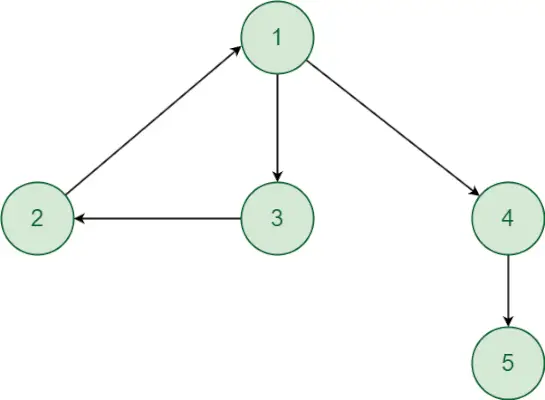
Przyjrzyjmy się podejściu na podstawie następującego przykładu:

przykładowy rysunek

  • Zaczynając od wierzchołka 1. Istnieje ścieżka od wierzchołka 1 do wierzchołka 2 i odwrotnie. Podobnie istnieje ścieżka z wierzchołka 1 do wierzchołka 3 i odwrotnie. Zatem wierzchołek 2 i 3 będą w tym samym silnie połączonym komponencie co wierzchołek 1. Chociaż istnieje skierowana ścieżka z wierzchołka 1 do wierzchołka 4 i wierzchołka 5. Ale nie ma skierowanej ścieżki z wierzchołka 4,5 do wierzchołka 1, więc wierzchołek 4 i 5 nie będą znajdować się w tym samym silnie połączonym komponencie co wierzchołek 1. Zatem wierzchołki 1,2 i 3 tworzą silnie połączony komponent.
  • Dla wierzchołków 2 i 3 określono już komponent silnie połączony.
  • W przypadku wierzchołka 4 istnieje ścieżka z wierzchołka 4 do wierzchołka 5, ale nie ma ścieżki z wierzchołka 5 do wierzchołka 4. Zatem wierzchołki 4 i 5 nie będą w tym samym silnie połączonym komponencie. Zatem zarówno wierzchołek 4, jak i wierzchołek 5 będą częścią pojedynczego, silnie połączonego komponentu.
  • Zatem będą 3 silnie połączone komponenty {1,2,3}, {4} i {5}.

Poniżej znajduje się implementacja powyższego podejścia:

C++ 
#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& przym., wektor & vis) { // Jeśli węzeł curr jest miejscem docelowym, zwróć wartość true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } zwróć fałsz;  } // Aby sprawdzić, czy istnieje ścieżka od źródła do // miejsca docelowego bool isPath(int src, int des, wektor>& przym) { wektor vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funkcja zwracająca wszystkie // silnie powiązane komponenty grafu.  wektor> findSCC(int n, wektor>& a) { // Przechowuje wszystkie silnie połączone komponenty.  wektor> odpowiedzi;  // Przechowuje, czy wierzchołek jest częścią wektora silnie // połączonego komponentu is_scc(n + 1, 0);  wektor> przym(n + 1);  for (int i = 0; tj< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector sc;  scc.push_back(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> krawędzie{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  wektor> ans = obj.findSCC(V, krawędzie);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>
Jawa 
import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> przym., lista vis) { // Jeśli węzeł curr jest miejscem docelowym, zwróć wartość true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } zwróć fałsz;  } // Aby sprawdzić, czy istnieje ścieżka od źródła do // miejsca docelowego. boolean isPath(int src, int des, List> przym.) { Lista vis = nowa ArrayList(adj.size() + 1);  for (int i = 0; tj<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, Lista> a) { // Przechowuje wszystkie silnie połączone komponenty.  Lista> ans = nowa ArrayList();  // Przechowuje, czy wierzchołek jest częścią jakiejś silnie // połączonej listy komponentów is_scc = nowa ArrayList(n + 1);  for (int i = 0; tj<= n; i++) {  is_scc.add(0);  }  List> adj = nowa ArrayList();  for (int i = 0; tj<= n; i++) {  adj.add(new ArrayList());  }  for (List krawędź : a) { przym.get(edge.get(0)).add(edge.get(1));  } // Przechodzenie przez wszystkie wierzchołki for (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = nowa ArrayList();  scc.add(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> krawędzie = nowa ArrayList();  krawędzie.add(new ArrayList(List.of(1, 3)));  krawędzie.add(new ArrayList(List.of(1, 4)));  krawędzie.add(new ArrayList(List.of(2, 1)));  krawędzie.add(new ArrayList(List.of(3, 2)));  krawędzie.add(new ArrayList(List.of(4, 5)));  Lista> ans = obj.findSCC(V, krawędzie);  System.out.println('Silnie połączone komponenty to:');  dla (Lista x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Ten kod został stworzony przez shivamgupta310570>
Pyton 
class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>
C# 
using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> przym., lista vis) { // Jeśli miejscem docelowym jest węzeł curr, zwróć wartość true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } zwróć fałsz;  } // Aby sprawdzić, czy istnieje ścieżka od źródła do miejsca docelowego public bool IsPath(int src, int des, List> przym) { var show = nowa lista (przym. Liczba + 1);  for (int i = 0; tj< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> ZnajdźSCC(int n, Lista> a) { // Przechowuje wszystkie silnie połączone komponenty var ans = new List>();  // Przechowuje informację, czy wierzchołek jest częścią silnie połączonego komponentu var isScc = new List (n + 1);  for (int i = 0; tj< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  for (int i = 0; tj< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Dodaj(i);  for (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> krawędzie = nowa lista> {nowa lista { 1, 3 }, nowa lista { 1, 4 }, nowa lista { 2, 1 }, nowa lista { 3, 2 }, nowa lista {4, 5}};  Lista> ans = obj.FindSCC(V, krawędzie);  Console.WriteLine('Silnie połączone komponenty to:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Konsola.WriteLine();  } } } // Ten kod został napisany przez shivamgupta310570>
JavaScript 
class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  dla (niech i = 0; tj< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>
Wyjście 
Strongly Connected Components are: 1 2 3 4 5>

Złożoność czasowa: O(n * (n + m)), ponieważ dla każdej pary wierzchołków sprawdzamy, czy istnieje między nimi ścieżka.
Przestrzeń pomocnicza: O(N)

to znak specjalny

Efektywne podejście do wyszukiwania silnie połączonych komponentów (SCC)

Aby znaleźć SCC na wykresie, możemy użyć algorytmów takich jak Algorytm Kosaraju Lub Algorytm Tarjana . Przyjrzyjmy się tym algorytmom krok po kroku.

1. Algorytm Kosaraju :

Algorytm Kosaraju składa się z dwóch głównych faz:

  1. Wykonywanie wyszukiwania w głąb (DFS) na oryginalnym wykresie :
    • Najpierw wykonujemy DFS na oryginalnym wykresie i rejestrujemy czasy zakończenia węzłów (tj. czas, w którym DFS kończy całkowite eksplorowanie węzła).
  2. Wykonywanie DFS na transponowanym wykresie :
    • Następnie odwracamy kierunek wszystkich krawędzi na wykresie, aby utworzyć wykres transponowany.
    • Następnie wykonujemy DFS na transponowanym grafie, rozważając węzły w malejącej kolejności ich czasów zakończenia zarejestrowanych w pierwszej fazie.
    • Każde przejście DFS w tej fazie da nam jeden SCC.

Oto uproszczona wersja algorytmu Kosaraju:

  1. DFS na oryginalnym wykresie : Rekordowy czas ukończenia.
  2. Transponuj wykres : Odwróć wszystkie krawędzie.
  3. DFS na transponowanym wykresie : Węzły przetwarzania w kolejności malejącego czasu zakończenia w celu znalezienia SCC.

2. Algorytm Tarjana :

Algorytm Tarjana jest bardziej wydajny, ponieważ znajduje SCC w jednym przebiegu DFS przy użyciu stosu i dodatkowej księgowości:

  1. Przejście DFS : Podczas DFS utrzymuj indeks dla każdego węzła i najmniejszy indeks (wartość najniższego łącza), do którego można uzyskać dostęp z węzła.
  2. Stos : Śledź węzły znajdujące się aktualnie na stosie rekurencji (część aktualnie badanego SCC).
  3. Identyfikacja SCC : Kiedy wartość dolnego łącza węzła jest równa jego indeksowi, oznacza to, że znaleźliśmy SCC. Usuń wszystkie węzły ze stosu, aż dotrzemy do bieżącego węzła.

Oto uproszczony zarys algorytmu Tarjana:

  1. Zainicjujindex>do 0.
  2. Dla każdego nieodwiedzonego węzła wykonaj DFS.
    • Ustaw indeks węzła i wartość dolnego łącza.
    • Wciśnij węzeł na stos.
    • Dla każdego sąsiedniego węzła wykonaj DFS, jeśli nie jest odwiedzany, lub zaktualizuj wartość dolnego łącza, jeśli znajduje się na stosie.
    • Jeśli wartość najniższego łącza węzła jest równa jego indeksowi, usuń węzły ze stosu, tworząc SCC.

Wniosek

Zrozumienie i odnalezienie silnie połączone elementy na grafie skierowanym jest niezbędna w wielu zastosowaniach w informatyce. Kosaraju I Tarjana Algorytmy są skutecznymi sposobami identyfikacji SCC, każdy z własnym podejściem i zaletami. Opanowując te koncepcje, możesz lepiej analizować i optymalizować strukturę i zachowanie złożonych sieci.