Powierzchnia pryzmatu: W matematyce pryzmat jest istotnym członkiem rodziny wielościanów i jest definiowany jako trójwymiarowy kształt składający się z dwóch identycznych wielokątów skierowanych ku sobie, połączonych bocznie prostokątnymi lub równoległobocznymi ścianami. Identycznymi wielokątami mogą być trójkąty, kwadraty, prostokąty, pięciokąty lub dowolny inny wielokąt o n-bocznych stronach i nazywane są podstawami pryzmatu. Pozostałe ściany pryzmatu to równoległoboki lub prostokąty.
W tym artykule omówimy różne typy pryzmatów i wzór na pole powierzchni pryzmatu wraz z przykładami i problemami praktycznymi.
Spis treści
- Jaka jest powierzchnia pryzmatu?
- Różne typy pryzmatów
- Pole powierzchni wzoru pryzmatu
- Pole powierzchni pryzmatu rozwiązane przykłady
- Ćwicz problemy dotyczące powierzchni pryzmatu
Jaka jest powierzchnia pryzmatu?
Pole powierzchni pryzmatu określa się jako całkowitą powierzchnię ujętą przez wszystkie jego ściany. Aby określić pole powierzchni pryzmatu, musimy obliczyć pola każdej z jego ścian, a następnie dodać powstałe pola. Pryzmat ma dwa rodzaje powierzchni, mianowicie powierzchnię boczną i powierzchnię całkowitą. Obszar zajmowany przez ściany pryzmatu, z wyłączeniem dwóch równoległych ścian (podstaw pryzmatu), nazywany jest jego powierzchnią boczną.
Pole powierzchni bocznej pryzmatu = [obwód podstawy × wysokość] jednostki kwadratowe
Całkowita powierzchnia pryzmatu jest sumą pól jego dwóch podstaw i powierzchni bocznej.
Ogólny wzór na obliczenie całkowitego pola powierzchni dowolnego typu prawego pryzmatu to:
Całkowita powierzchnia pryzmatu = [2 (powierzchnia podstawowa) + (obwód podstawy × wysokość)] jednostek kwadratowych
Różne typy pryzmatów
Istnieją różne typy pryzmatów w zależności od kształtu podstawy pryzmatu, np
- Pryzmaty trójkątne,
- Pryzmaty kwadratowe,
- Pryzmaty prostokątne,
- Pryzmaty pięciokątne,
- Pryzmaty sześciokątne,
- Pryzmaty ośmiokątne.
Trójkątny pryzmat
Pryzmat o podstawie trójkątnej nazywany jest pryzmatem trójkątnym. Trójkątny pryzmat składa się z trzech nachylonych prostokątnych powierzchni i dwóch równoległych podstaw trójkąta. Niech H będzie wysokością trójkątnego pryzmatu; a, b i c to długości boków, a h to wysokość podstaw trójkąta.
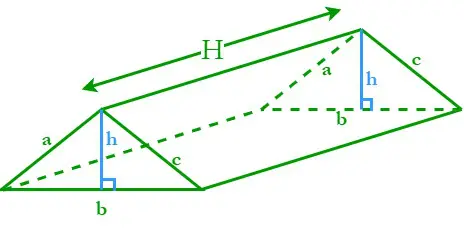
Obwód podstawy trójkąta (P) = Suma jego trzech boków = a + b + c
Pole podstawy trójkąta (A) = ½ × podstawa × wysokość = ½ bh
Wiemy, że ogólny wzór na pole powierzchni bocznej prawego pryzmatu wynosi L.S.A. = PH, gdzie P jest obwodem podstawy, a A jest polem podstawy.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy ,
Pole powierzchni bocznej trójkątnego pryzmatu = (a + b +c)H jednostki kwadratowe
Gdzie,
a, b, c są bokami podstawy trójkąta
H jest wysokością trójkątnego pryzmatu
Wiemy, że ogólny wzór na całkowitą powierzchnię prawego pryzmatu to: T. S. A. = PH+2A, gdzie P jest obwodem podstawy, A jest polem podstawy, a H jest wysokością pryzmatu.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy
Całkowita powierzchnia trójkątnego pryzmatu = (a + b + c)H + 2 × (½ bh)
Całkowita powierzchnia trójkątnego pryzmatu = (a + b + c)H + bh jednostki kwadratowe
Gdzie,
a, b, c są bokami podstawy trójkąta
H jest wysokością trójkątnego pryzmatu
h jest wysokością trójkąta
Prostopadłościan
Pryzmat o podstawie prostokątnej nazywany jest pryzmatem prostokątnym. Prostopadłościan składa się z czterech prostokątnych powierzchni i dwóch równoległych prostokątnych podstaw. Niech wysokość pryzmatu będzie wynosić h, a długość i szerokość jego prostokątnych podstaw odpowiednio l i w .

Obwód podstawy prostokątnej (P) = Suma jej czterech boków = 2 (l + w)
Pole podstawy prostokąta (A) = długość × szerokość = l × szer
Wiemy, że ogólny wzór na pole powierzchni bocznej prawego pryzmatu to L.S.A. = PH, gdzie P jest obwodem podstawy, a A jest polem podstawy.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy ,
Pole powierzchni bocznej prostopadłościanu = 2h(l + w) jednostek kwadratowych
Gdzie,
l to długość
w to szerokość
h to wzrost
Wiemy, że ogólny wzór na całkowite pole powierzchni prawego pryzmatu to T. S. A. = PH+2A, gdzie P to obwód podstawy, A to pole podstawy, a H to wysokość pryzmatu.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy
Całkowita powierzchnia prostopadłościanu = 2h(l + w) + 2(l × w)
= 2 lh + 2 biale + 2 lw
Całkowita powierzchnia prostopadłościanu = 2 (lh + wh + lw) jednostek kwadratowych
Gdzie,
l to długość
w to szerokość
h to wzrost
Pryzmat kwadratowy
Pryzmat o podstawie kwadratowej nazywany jest pryzmatem kwadratowym. Pryzmat kwadratowy składa się z czterech prostokątnych powierzchni i dwóch równoległych kwadratowych podstaw. Niech wysokość pryzmatu będzie wynosić h, a długość jego podstaw kwadratowych będzie wynosić s.

Obwód podstawy kwadratu (P) = Suma jego czterech boków = s + s + s + s = 4s
Pole podstawy kwadratu (A) = (długość boku)2= s2
Wiemy, że ogólny wzór na pole powierzchni bocznej prawego pryzmatu to L.S.A. = PH, gdzie P jest obwodem podstawy, a A jest polem podstawy.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy,
Pole powierzchni bocznej pryzmatu kwadratowego = 4 jednostki kwadratowe
Gdzie,
s to bok podstawy kwadratu
h jest wysokością kwadratowego pryzmatu
Wiemy, że ogólny wzór na całkowitą powierzchnię prawego pryzmatu to: T. S. A. = PH+2A, Gdzie P to obwód podstawy, A to pole podstawy, a H to wysokość pryzmatu.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy
Całkowita powierzchnia kwadratowego pryzmatu = [4sh + 2s 2 ] jednostki kwadratowe
Gdzie,
s to bok podstawy kwadratu
h jest wysokością kwadratowego pryzmatu
Pryzmat pięciokątny
Pryzmat o podstawie pięciokątnej nazywany jest pryzmatem pięciokątnym. Pryzmat pięciokątny składa się z pięciu nachylonych prostokątnych powierzchni i dwóch równoległych pięciokątnych podstaw. Niech h będzie wysokością pięciokątnego pryzmatu; a i b będą długością apotemów i długościami boków podstaw pięciokąta.

Obwód podstawy pięciokąta (P) = Suma jego pięciu boków = 5b
Pole podstawy pięciokąta (A) = 5/2 x (długość apotemu) x (długość boku) = 5ab
Wiemy, że ogólny wzór na pole powierzchni bocznej prawego pryzmatu to L.S.A. = PH, gdzie P jest obwodem podstawy, a A jest polem podstawy.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy,
Pole powierzchni bocznej pryzmatu pięciokątnego = 5 bh jednostek kwadratowych
Gdzie,
b jest bokiem podstawy pięciokąta
h jest wysokością pięciokątnego pryzmatu
Wiemy, że ogólny wzór na całkowite pole powierzchni prawego pryzmatu to T. S. A. = PH+2A, gdzie P to obwód podstawy, A to pole podstawy, a H to wysokość pryzmatu.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy,
Całkowita powierzchnia pryzmatu pięciokątnego = [5bh + 5ab] jednostek kwadratowych
Gdzie,
b jest bokiem podstawy pięciokąta
a jest długością apotemów.
h jest wysokością pięciokątnego pryzmatu
Sześciokątny pryzmat
Pryzmat o podstawie sześciokątnej nazywany jest pryzmatem sześciokątnym. Sześciokątny pryzmat składa się z sześciu nachylonych prostokątnych powierzchni i dwóch równoległych sześciokątnych podstaw. Niech h będzie wysokością sześciokątnego pryzmatu; a będą długościami boków podstaw sześciokątnych.

Obwód podstawy sześciokąta (P) = Suma jego sześciu boków = 6a
Pole podstawy sześciokąta (A) = 6 x (Pole trójkąta równobocznego)
A = 6 x (√3a2/4) ⇒ ZA = 3√3a2/2
Wiemy, że ogólny wzór na pole powierzchni bocznej prawego pryzmatu to L.S.A. = PH, gdzie P jest obwodem podstawy, a A jest polem podstawy.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy,
Pole powierzchni bocznej sześciokątnego pryzmatu = 6ah jednostek kwadratowych
Gdzie,
a to bok sześciokątnej podstawy
h jest wysokością sześciokątnej podstawy
Wiemy, że ogólny wzór na całkowite pole powierzchni prawego pryzmatu to T. S. A. = PH+2A, gdzie P to obwód podstawy, A to pole podstawy, a H to wysokość pryzmatu.
Zastępując wszystkie wartości we wzorze ogólnym, otrzymujemy
Całkowita powierzchnia sześciokątnego pryzmatu = [6ah +3√3a2] jednostki kwadratowe
Gdzie,
a to bok sześciokątnej podstawy
h jest wysokością sześciokątnej podstawy:
Pole powierzchni wzoru pryzmatu
Poniższa tabela zawiera wzory dla różnych typów pryzmatów:
Kształt | Podstawa pryzmatu | Powierzchnia boczna[Obwód podstawy × wysokość] | Całkowita powierzchnia[(2 × powierzchnia bazowa) + (obwód podstawy × wysokość)] |
|---|---|---|---|
Trójkątny pryzmat | Trójkąt ciągi Javy | (a + b +c)H jednostki kwadratowe | (a + b + c)H + bh jednostki kwadratowe |
Prostopadłościan | Prostokąt | 2h(l + w) jednostek kwadratowych | 2 (lh + wh + lw) jednostki kwadratowe |
Pryzmat kwadratowy | Kwadrat | 4sh jednostki kwadratowe | [4sh + 2s2] jednostki kwadratowe |
Pryzmat pięciokątny | Pięciokąt | Jednostki kwadratowe 5bh | [5ab + 5bh] jednostki kwadratowe |
Sześciokątny pryzmat | Sześciokąt | Jednostki kwadratowe 6ah | [3√3a2+ 6ah] jednostki kwadratowe |
Pole powierzchni pryzmatu rozwiązane przykłady
Zadanie 1: Jaka jest wysokość pryzmatu, którego powierzchnia podstawy wynosi 36 jednostek kwadratowych, obwód podstawy wynosi 24 jednostki, a powierzchnia całkowita wynosi 320 jednostek kwadratowych?
Rozwiązanie:
Biorąc pod uwagę dane,
Powierzchnia podstawy = 36 jednostek kwadratowych
Obwód podstawy = 24 jednostki
Całkowita powierzchnia pryzmatu = 320 jednostek kwadratowych
Mamy,
Całkowita powierzchnia pryzmatu = (2 × powierzchnia podstawy) + (obwód podstawy × wysokość)
⇒ 320 = (2 × 36)+ (24 × godz.)
⇒ 24h = 248 ⇒ h = 10,34 jednostki
Zatem wysokość danego pryzmatu wynosi 10,34 jednostki.
Zadanie 2: Znajdź całkowite pole powierzchni kwadratowego pryzmatu, jeśli wysokość pryzmatu i długość boku kwadratu wynoszą odpowiednio 13 cm i 4 cm.
Rozwiązanie:
Biorąc pod uwagę dane,
Wysokość kwadratowego pryzmatu (h) = 13 cm
Długość boku kwadratowej podstawy (a) = 4 cm
Wiemy to,
Całkowita powierzchnia kwadratowego pryzmatu = 2a2+ 4ah
= 2 × (4)2+ 4 × 4 × 13
= 32 + 208 = 240 cm2
Zatem całkowita powierzchnia danego pryzmatu wynosi 240 cm2.
Zadanie 3: Określ długość podstawy pięciokątnego pryzmatu, jeśli jego całkowite pole wynosi 100 jednostek kwadratowych, a jego wysokość i długość apothemu wynoszą odpowiednio 8 jednostek i 5 jednostek.
Rozwiązanie:
Biorąc pod uwagę dane,
Całkowita powierzchnia pryzmatu pięciokątnego = 100 jednostek kwadratowych
Wysokość pryzmatu (h) = 8 jednostek
Długość apotem (a) = 5 jednostek
Wiemy to,
Całkowita powierzchnia pryzmatu pięciokątnego = 5ab + 5bh
⇒ 100 = 5b (a+ godz)
⇒ 100/5 = b (5 + 8)
⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 jednostki
Zatem długość podstawy wynosi 1,54 jednostki
Problem 4: Oblicz wysokość graniastosłupa prostokątnego i pole całkowite prostopadłościanu, jeśli jego powierzchnia boczna wynosi 540 cm2, a długość i szerokość podstawy wynoszą odpowiednio 13 cm i 7 cm.
Rozwiązanie:
myflixr
Biorąc pod uwagę dane,
Długość prostokątnej podstawy (l) = 13 cm
Szerokość prostokątnej podstawy (w) = 7 cm
Pole powierzchni bocznej pryzmatu = 540 cm2
Mamy,
Pole powierzchni bocznej pryzmatu = obwód podstawy × wysokość
⇒ 540 = 2 (l + w) godz
⇒ 2 (13 + 7) godz. = 540
⇒ 2 (20) godz. = 540 ⇒ godz. = 13,5 cm
Wiemy to,
Całkowita powierzchnia prostopadłościanu = 2 (lw + wh + lh)
= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))
= 2 × (91 + 94,5 + 175,5) = 722 cm2
Zatem wysokość i całkowite pole powierzchni danego prostopadłościanu wynoszą odpowiednio 13,5 cm i 722 cm2.
Zadanie 5: Określ pole powierzchni regularnego graniastosłupa sześciokątnego, jeśli wysokość pryzmatu wynosi 12 cali, a długość boku podstawy wynosi 5 cali.
Rozwiązanie:
Biorąc pod uwagę dane,
Wysokość pryzmatu (h) = 12 cali
Długość boku podstawy (a) = 6 cali
Pole powierzchni regularnego graniastosłupa sześciokątnego = 6ah + 3√3a2
= 6 × 5 × 12 + 3√3(5)2
= 360 + 75√3
= 360 + 75 × (1,732) = 489,9 cala kwadratowego
Zatem powierzchnia danego pryzmatu wynosi 489,9 cala kwadratowego.
Zadanie 6: Oblicz pole powierzchni bocznej i całkowitej trójkątnego pryzmatu, którego obwód podstawy wynosi 25 cali, długość podstawy i wysokość trójkąta wynoszą 9 cali i 10 cali, a wysokość pryzmatu wynosi 14 cali.
Rozwiązanie:
Biorąc pod uwagę dane,
Wysokość pryzmatu (H) = 14 cali
Obwód podstawy pryzmatu (P) = 25 cali
Długość podstawy trójkąta = 9 cali
Wysokość trójkąta = 10 cali
Wiemy to,
Pole powierzchni bocznej pryzmatu = obwód podstawy × wysokość
= 25 × 14 = 350 cali kwadratowych
Pole podstawy trójkąta (A) = ½ × podstawa × wysokość = 1/2 × 9 × 10 = 45 cali kwadratowych
Całkowita powierzchnia trójkątnego pryzmatu = 2A + PH
= 2 × 45 + 25 × 14 = 90 + 350 = 440 cali kwadratowych
Zatem powierzchnia boczna i całkowita pryzmatu wynoszą odpowiednio 350 cali kwadratowych i 440 cali kwadratowych.
Ćwicz problemy dotyczące powierzchni pryzmatu
1. Biorąc pod uwagę prostopadłościan o wymiarach:
- Długość = 6 cm
- Szerokość = 4 cm
- Wysokość = 5 cm
Oblicz całkowitą powierzchnię.
2. Rozważ trójkątny pryzmat o wymiarach:
- Podstawa trójkąta = 8 cm
- Wysokość trójkąta = 6 cm
- Długość pryzmatu = 10 cm
Znajdź całkowitą powierzchnię.
3. Wyznacz pole powierzchni pięciokątnego pryzmatu foremnego za pomocą:
- Długość boku podstawy = 7 cm
- Wysokość pryzmatu = 9 cm.
4. Oblicz pole powierzchni sześciokątnego pryzmatu ze wzoru:
- Długość boku regularnej sześciokątnej podstawy = 10 cm
- Wysokość pryzmatu = 12 cm.
Powierzchnia pryzmatu – często zadawane pytania
Co to jest pryzmat w geometrii?
Pryzmat to trójwymiarowy kształt z dwiema przystającymi równoległymi podstawami i łączącymi je prostokątnymi lub równoległobocznymi ścianami bocznymi. Pryzmaty występują w różnych formach, takich jak pryzmaty prostokątne, pryzmaty trójkątne i pryzmaty pięciokątne, każdy z unikalnymi cechami.
Jak znaleźć powierzchnię pryzmatu?
Aby obliczyć pole powierzchni pryzmatu, oblicz pola wszystkich jego ścian i zsumuj je. W przypadku prostopadłościanu wzór na pole powierzchni wynosi 2lw + 2lh + 2wh, gdzie l to długość, w to szerokość, a h to wysokość. W przypadku innych typów pryzmatów, takich jak pryzmaty trójkątne lub pięciokątne, mogą być potrzebne dodatkowe wzory na powierzchnię podstawy i powierzchnię boczną.
Jakie są właściwości pryzmatu?
Pryzmaty mają kilka kluczowych właściwości:
- Mają dwie przystające, równoległe podstawy.
- Wszystkie ściany boczne są równoległobokami.
- Wysokość (wysokość) to prostopadła odległość między dwiema podstawami.
- Podstawy mają identyczny kształt i rozmiar.
- Przekrój równoległy do podstaw ma zawsze taki sam kształt i rozmiar jak podstawy.
Jakie są przykłady pryzmatów z życia wziętych?
Pryzmaty można spotkać w różnych przedmiotach i konstrukcjach codziennego użytku. Przykłady obejmują:
- Prostokątne pryzmaty: Budynki, pudełka po płatkach śniadaniowych, książki.
- Pryzmaty trójkątne: Dachy domów, obiekty w kształcie klina.
- Pryzmaty pięciokątne: Niektóre typy kolumn, niektóre konstrukcje architektoniczne.
- Pryzmaty sześciokątne: Niektóre rodzaje kryształów, niektóre pojemniki opakowaniowe.
Dlaczego powierzchnia jest ważna w pryzmatach?
Pole powierzchni ma kluczowe znaczenie w pryzmatach, ponieważ reprezentuje całkowitą powierzchnię wszystkich powierzchni (ścian) pryzmatu. Zrozumienie pola powierzchni pomaga w różnych praktycznych zastosowaniach, takich jak obliczanie ilości materiału potrzebnego do zbudowania lub pokrycia obiektu w kształcie pryzmatu, określenie współczynnika przenikania ciepła i optymalizacja projektu opakowania.
