Trygonometria jest ważną gałęzią matematyki zajmującą się zależnością między kątami i długościami boków trójkąta prostokątnego. Sześć stosunków lub funkcji trygonometrycznych to sinus, cosinus, tangens, cosecans i secans, a stosunek trygonometryczny to stosunek boków trójkąta prostokątnego. Funkcje sinus, cosinus i tangens to trzy ważne funkcje trygonometryczne, ponieważ pozostałe trzy, tj. funkcje cosecans, secans i cotangens, są funkcjami odwrotności odpowiednio funkcji sinus, cosinus i tangens.
- sin θ = strona przeciwna/przeciwprostokątna
- cos θ = sąsiadujący bok/przeciwprostokątna
- tan θ = strona przeciwna/strona sąsiadująca
- cosec θ = przeciwprostokątna/strona przeciwna
- sec θ = Przeciwprostokątna/przylegająca strona
- łóżko θ = strona sąsiadująca/strona przeciwna
Funkcja styczna jest jedną z 6 funkcji trygonometrycznych używanych w wzory trygonometryczne .
Spis treści
Wzór styczny
Tangens kąta w trójkącie prostokątnym to stosunek długości przeciwległego boku do długości sąsiedniego boku danego kąta. Funkcję styczną zapisujemy jako tangens. Rozważmy trójkąt prostokątny XYZ, którego jeden z kątów ostrych wynosi θ. Strona przeciwna to strona przeciwna do kąta θ, a strona sąsiadująca to strona przylegająca do kąta θ.
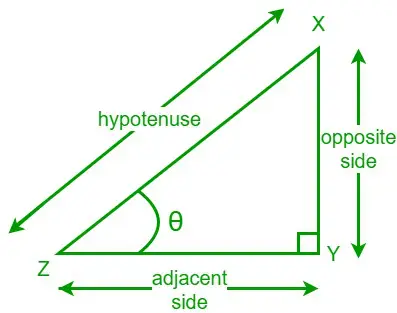
Teraz wzór na tangens dla danego kąta θ to:
tan θ = strona przeciwna/strona sąsiadująca
Niektóre podstawowe wzory styczne
Funkcja styczna w ćwiartkach
Funkcja tangensa jest dodatnia w pierwszej i trzeciej ćwiartce oraz ujemna w drugiej i czwartej ćwiartce.
- tan (2π + θ) = tan θ (1ulkwadrant)
- tan (π – θ) = – tan θ (2IIkwadrant)
- tan (π + θ) = tan θ (3r & Dkwadrant)
- tan (2π – θ) = – tan θ (4tkwadrant)
Funkcja styczna jako funkcja ujemna
Funkcja styczna jest funkcją ujemną, ponieważ tangens kąta ujemnego jest ujemną stycznej kąta dodatniego.
tan (-θ) = – tan θ
Funkcja styczna w kategoriach funkcji sinus i cosinus
Funkcję styczną w postaci funkcji sinus i cosinus można zapisać jako:
tan θ = sin θ/cos θ
Wiemy, że tan θ = strona przeciwna/strona sąsiadująca
Teraz podziel licznik i mianownik przez przeciwprostokątną
tan θ = (strona przeciwna/przeciwprostokątna)/(strona sąsiadująca/przeciwprostokątna)
Wiemy, że sin θ = przeciwna strona/przeciwprostokątna
cos θ = sąsiedni bok/przeciwprostokątna
Zatem tan θ = sin θ/cos θ
Funkcja styczna w kategoriach funkcji sinus
Funkcję styczną w odniesieniu do funkcji sinus można zapisać jako:
tan θ = sin θ/(√1 – grzech 2 I)
Wiemy to,
tan θ = sin θ/cos θ
es5 kontra es6
Z tożsamości pitagorejskich mamy:
bez2θ + sałata2θ = 1
sałata2θ = 1 – grzech2I
cos θ = √(1 – grzech2I)
Zatem tan θ = sin θ/(√1 – sin2I)
Funkcja styczna w kategoriach funkcji cosinus
Funkcję styczną w funkcji cosinus można zapisać jako:
tan θ = (√1 -cos 2 ja)/bo i
Wiemy to,
tan θ = sin θ/cos θ
Z tożsamości pitagorejskich mamy:
bez2θ + sałata2θ = 1
bez2θ = 1 – sałata2I
grzech θ = √(1 – sałata2I)
Zatem tan θ = (√1 – cos2ja)/bo i
Funkcja styczna w kategoriach funkcji cotangens
Funkcję styczną w odniesieniu do funkcji cotangens można zapisać jako:
tan θ = 1/łóżeczko θ
Lub
tan θ = łóżeczko (90° – θ) (lub) łóżeczko (π/2 – θ)
Funkcja styczna w kategoriach funkcji cosecans
Funkcję styczną w odniesieniu do funkcji cosecans można zapisać jako:
tan θ = 1/√(cosec 2 ja – 1)
Z tożsamości pitagorejskich mamy:
cosek2θ – łóżeczko2θ = 1
łóżko składane2θ = cosek2ja – 1
łóżko θ = √(cosec2ja – 1)
Wiemy to,
tan θ = 1/łóżeczko θ
Zatem tan θ = 1/√(cosec2ja – 1)
Funkcja styczna w kategoriach funkcji siecznej
Funkcję styczną w odniesieniu do funkcji siecznej można zapisać jako:
tan θ = √ sek 2 ja – 1
Z tożsamości pitagorejskich mamy:
sek2θ – tak2θ = 1
tan θ = sek2ja – 1
Zatem tan θ = √(sek2ja – 1)
Funkcja styczna w kategoriach podwójnego kąta
Funkcja tangensa dla kąta podwójnego to:
tan 2θ = (2 tan θ)/(1 – tan 2 I)
Funkcja styczna w kategoriach potrójnego kąta
Funkcja tangensa dla potrójnego kąta to:
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 opalenizna 2 I)
Funkcja styczna w kategoriach półkąta
Funkcja styczna dla półkąta to:
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Funkcja styczna w zakresie dodawania i odejmowania dwóch kątów
Wzory na sumę i różnicę funkcji stycznej to:
tan (A + B) = (brązowy A + brązowy B)/(1 – brązowy A brązowy B)
brązowy (A – B) = (brązowy A – brązowy B)/(1 + brązowy A brązowy B)
Tabela współczynników trygonometrycznych
| Kąt (w stopniach) | Kąt (w radianach) | grzech I | bo θ | tan θ = sin θ/cos θ | cosec θ | sek. θ | łóżeczko ja |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Nieokreślony | 1 | Nieokreślony |
| 30° | str. 6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | s./4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | s./3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 testy regresyjne w testowaniu oprogramowania | 23 | 2 | 1/√3 |
| 90° | str./2 | 1 | 0 | 1/0 = nieokreślony | 1 | Nieokreślony | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Liczba Pi | 0 | -1 | 0/(-1) = 0 | Nieokreślony | -1 | Nieokreślony |
Rozwiązany przykład na formułach stycznych
Przykład 1: Znajdź wartość tan θ, jeśli sin θ = 2/5 i θ jest kątem w pierwszej ćwiartce.
Rozwiązanie:
Dany,
- grzech θ = 2/5
Z tożsamości pitagorejskich, które mamy,
bez2θ + sałata2θ = 1
sałata2θ = 1 – grzech2θ = 1 – (2/5)2
sałata2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Ponieważ θ jest kątem w pierwszej ćwiartce, cos θ jest dodatnie.
cos θ = √21/5
Wiemy to,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Zatem wartość tan θ, gdy sin θ = 2/5 i θ znajduje się w pierwszej ćwiartce, wynosi (2√21) /(21)
Przykład 2: Znajdź wartość tan x, jeśli sec x = 13/12 i x jest kątem w czwartej ćwiartce.
Rozwiązanie:
Biorąc pod uwagę, s x = 13/12
Z tożsamości pitagorejskich mamy:
sek2x- tak2x = 1
Więc2x = sek2x – 1= (13/12)2- 1
Więc2x = (169/144) – 1 = 25/144
tan x = ± 5/12
Ponieważ x jest kątem w czwartej ćwiartce, tg x jest ujemne.
tan x = – 5/12
Stąd, tan x = – 5/12
Przykład 3: Jeśli tan X = 2/3 i tan Y = 1/2, to jaka jest wartość tan (X + Y)?
Rozwiązanie:
Dany,
tan X = 2/3 i tan Y = 1/2
Wiemy to,
tan (X + Y) = (brązowy X + tan Y)/(1 – brązowy X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Stąd, tan(X + Y) = 7/4
Przykład 4: Oblicz funkcję styczną, jeśli sąsiednie i przeciwne boki trójkąta prostokątnego mają odpowiednio 4 cm i 7 cm.
Rozwiązanie:
chmod 755
Dany,
Sąsiedni bok = 4 cm
Przeciwna strona = 7 cm
Wiemy to,
tan θ = strona przeciwna/strona sąsiadująca
tan θ = 7/4 = 1,75
Stąd, tan θ = 1,75
Przykład 5: Mężczyzna patrzy na wieżę zegarową pod kątem 60° do szczytu wieży, której wysokość wynosi 100 m. Jaka jest odległość między człowiekiem a podstawą wieży?
Rozwiązanie:
Dany,
Wysokość wieży = 100 m i θ = 60°
Niech odległość człowieka od podnóża wieży = d
Mamy,
tan θ = strona przeciwna/strona sąsiadująca
opalenizna 60° = 100/d
√3 = 100/d [Ponieważ, więc 60° = √3]
d = 100/√3
Zatem odległość człowieka od podnóża wieży wynosi 100/√3
Przykład 6: Znajdź wartość tan θ, jeśli sin θ = 7/25 i sec θ = 25/24.
Rozwiązanie:
Dany,
grzech θ = 7/25
sekundy θ = 25/24
Wiemy to,
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Mamy,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Stąd, tan θ = 7/24
Przykład 7: Znajdź wartość tan θ, jeśli cosec θ = 5/3, a θ jest kątem w pierwszej ćwiartce.
Rozwiązanie:
Biorąc pod uwagę, cosec θ = 5/3
Z tożsamości pitagorejskich mamy:
szybkie sortowaniecosek2θ – łóżeczko2θ = 1
łóżko składane2θ = cosek2ja – 1
łóżeczko θ = (5/3)2– 1 = (25/9) – 1 = 16/9
łóżko θ = ±√16/9 = ± 4/3
Ponieważ θ jest kątem w pierwszej ćwiartce, zarówno funkcja cotangens, jak i styczna są dodatnie.
łóżeczko θ = 4/3
Wiemy to,
łóżko θ = 1/opalenizna θ
4/3 = 1/tanθ
tan θ = 3/4
Stąd, tan θ = 3/4
Przykład 8: Znajdź tan 3θ, jeśli sin θ = 3/7 i θ jest kątem w pierwszej ćwiartce.
Rozwiązanie :
Biorąc pod uwagę, grzech θ = 12/13
Z tożsamości pitagorejskich, które mamy,
bez2θ + sałata2θ = 1
sałata2θ = 1 – grzech2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Ponieważ θ jest kątem w pierwszej ćwiartce, cos θ jest dodatnie.
cos θ = 5/13
Wiemy to,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Stąd tan θ = 12/5
Teraz wiemy, że
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

