Objętość piramidy trójkątnej oblicza się ze wzoru V = 1/3A.H . Trójkątna piramida, znana również jako czworościan, to rodzaj piramidy o trójkątnej podstawie i trzech trójkątnych ścianach, które spotykają się w jednym punkcie zwanym wierzchołkiem.

W tym artykule dowiemy się szczegółowo o definicji piramidy, definicji piramidy trójkątnej, wzorze piramidy trójkątnej, przykładach i innych szczegółach.

Spis treści

• Co to jest piramida?
• Definicja piramidy trójkątnej
• Wzór piramidy trójkątnej
• Pole powierzchni trójkątnej piramidy
• Objętość trójkątnej piramidy

Co to jest piramida?

A piramida dzieli się na różne typy w zależności od kształtu podstawy, np. piramida trójkątna, piramida kwadratowa, piramida pięciokątna, piramida sześciokątna itp. Wierzchołek to miejsce styku powierzchni bocznych lub ścian bocznych piramidy . Prostopadła odległość od wierzchołka piramidy do środka jej podstawy to wysokość lub wysokość piramidy. Prostopadła odległość między wierzchołkiem a podstawą wysokości nachylenia powierzchni bocznej piramidy.

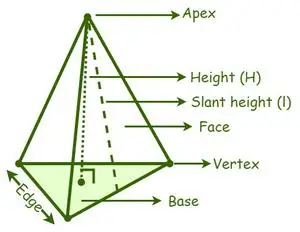
Piramida

Definicja piramidy trójkątnej

Trójkątna piramida to piramida, której podstawą jest trójkąt. Jest również znany jako czworościan i ma trzy trójkątne ściany i jedną trójkątną podstawę, przy czym trójkątna podstawa może być skalarna, równoramienna lub trójkąta równobocznego. Trójkąt dzieli się dalej na trzy typy, tj. regularną piramidę trójkątną, nieregularną piramidę trójkątną i piramidę trójkątną prostokątną.

• Regularna trójkątna piramida: Trójkątna piramida, której cztery ściany są trójkątami równobocznymi, nazywana jest regularną piramidą trójkątną. Ponieważ piramida składa się z trójkątów równobocznych, miara wszystkich jej kątów wewnętrznych wynosi 60°.

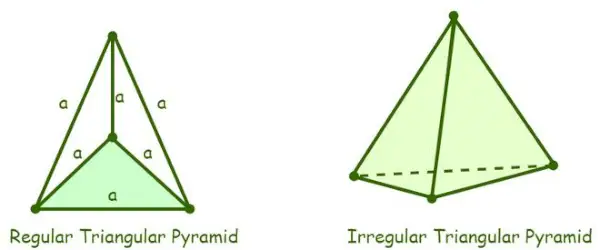
Definicja piramidy trójkątnej

• Nieregularna trójkątna piramida: Nieregularna piramida trójkątna to taka, której krawędzie podstawy nie są równe, tj. podstawą nieregularnej piramidy trójkątnej jest trójkąt pochyły lub trójkąt równoramienny. Zakłada się, że wszystkie piramidy trójkątne są regularnymi piramidami trójkątnymi, chyba że piramida trójkątna jest wyraźnie wymieniona jako nieregularna.

• Prawidłowa piramida trójkątna: Piramida trójkątna prostokątna to taka, której podstawa jest trójkątem prostokątnym, a wierzchołek znajduje się nad środkiem podstawy.

Wzór piramidy trójkątnej

Istnieją dwa wzory na piramidę trójkątną: pole powierzchni piramidy trójkątnej i objętość piramidy trójkątnej.

• Pole powierzchni trójkątnej piramidy
  • Pole powierzchni bocznej piramidy trójkątnej
  • Całkowita powierzchnia trójkątnej piramidy
• Objętość trójkątnej piramidy

Pole powierzchni trójkątnej piramidy

Pole powierzchni piramidy ma dwa rodzaje pól powierzchni, a mianowicie: pole powierzchni bocznej i pole powierzchni całkowitej, gdzie pole powierzchni piramidy jest sumą pól powierzchni bocznych lub ścian bocznych i pola podstawy piramidy.

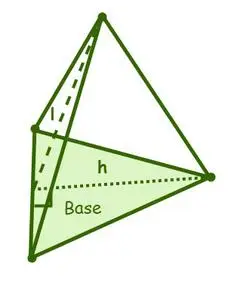
Pole powierzchni trójkątnej piramidy

Pole powierzchni bocznej piramidy trójkątnej

Pole powierzchni bocznej piramidy trójkątnej oblicza się ze wzoru:

Pole powierzchni bocznej piramidy trójkątnej (LSA) = ½ × obwód × wysokość nachylenia

Całkowita powierzchnia trójkątnej piramidy

Całkowita powierzchnia piramidy (TSA) = powierzchnia boczna piramidy + pole podstawy

Zatem TSA = ½ × obwód × wysokość nachylenia + ½ × podstawa × wysokość

Całkowita powierzchnia piramidy trójkątnej (TSA) = ½ × P × l + ½ bh

Gdzie,

• P to obwód podstawy
• l to wysokość nachylenia piramidy
• B jest podstawą trójkąta u podstawy
• H to wysokość piramidy

Objętość trójkątnej piramidy

Objętość piramidy to całkowita przestrzeń zawarta pomiędzy wszystkimi ścianami piramidy. Objętość piramidy jest zwykle oznaczana literą V, a jej wzór jest równy jednej trzeciej iloczynu pola podstawy i wysokości piramidy.

Wzór na objętość piramidy jest następujący:

Objętość trójkątnej piramidy = 1/3 × pole podstawy × wysokość

V = 1/3 × jednostka sześcienna AH

Gdzie,

• W to objętość piramidy
• A to pole podstawy piramidy
• H to wysokość lub wysokość piramidy

Wzór na objętość regularnej piramidy trójkątnej podano w następujący sposób

Objętość regularnej piramidy trójkątnej = a ³ /6√2 jednostek sześciennych

Gdzie A jestDługość krawędzi

Artykuł dotyczący piramidy trójkątnej:

• Prostokątna piramida
• Kwadratowa Piramida
• Piramida pięciokątna
• Sześciokątna piramida
• Objętość wzoru piramidy
• Pole powierzchni wzoru piramidy

Przykłady wzoru na piramidę trójkątną

Przykład 1: Określ objętość trójkątnej piramidy, której pole podstawy i wysokość wynoszą 50 cm ² i 12 cm, odpowiednio.

Rozwiązanie:

Biorąc pod uwagę dane,

• Pole podstawy trójkąta = 100 cm²
• Wysokość piramidy = 12 cm

Wiemy to,

Objętość trójkątnej piramidy (V) = 1/3 × pole podstawy trójkąta × wysokość

pasek narzędzi szybkiego dostępu do słów

wys. = 1/3 × 50 × 12 = 200 cm³

Zatem objętość danego trójkątnego ostrosłupa wynosi 200 cm³.

Przykład 2: Znajdź całkowitą powierzchnię regularnej trójkątnej piramidy, gdy długość każdej krawędzi wynosi 8 cali.

Rozwiązanie:

Biorąc pod uwagę dane,

• Długość każdej krawędzi regularnej trójkątnej piramidy (a) = 8 cali

Wiemy to,

Całkowita powierzchnia regularnej piramidy trójkątnej = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 cala kwadratowego

Zatem całkowita powierzchnia regularnej piramidy trójkątnej wynosi 110,851 cala kwadratowego.

Przykład 3: Określ objętość regularnej piramidy trójkątnej, której długość krawędzi wynosi 10 cm.

Rozwiązanie:

Biorąc pod uwagę dane,

• Długość każdej krawędzi regularnej piramidy trójkątnej (a) = 10 cm

Wiemy to,

Objętość regularnej piramidy trójkątnej = a³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Zatem objętość regularnej piramidy trójkątnej wynosi 117,85 cu. cm.

Przykład 4: Znajdź wysokość nachylenia trójkątnej piramidy, jeśli jej powierzchnia boczna wynosi 600 cali kwadratowych, a obwód podstawy wynosi 60 cali.

Rozwiązanie:

Biorąc pod uwagę dane,

• Powierzchnia boczna = 600 cali kwadratowych
• Obwód podstawy = 60 cali

Wiemy to,

Pole powierzchni bocznej = ½ × obwód × wysokość skosu

600 = ½ × 60 × l

l = 600/30 = 20 cali

Zatem wysokość nachylenia danej piramidy wynosi 20 cali.

Przykład 5: Oblicz całkowitą powierzchnię trójkątnej piramidy, której pole podstawy wynosi 28 cm2, obwód trójkąta wynosi 18 cm, a wysokość piramidy wynosi 20 cm.

Rozwiązanie:

Biorąc pod uwagę dane,

• Pole podstawy trójkąta = 28 cm²
• Wysokość skosu (l) = 20 cm
• Obwód (P) = 18 cm

Wiemy to,

Całkowita powierzchnia (TSA) piramidy trójkątnej = ½ × obwód × wysokość skosu + powierzchnia podstawy

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 cm2

Zatem całkowita powierzchnia danej piramidy wynosi 208 cm2.

Ćwicz problemy dotyczące wzoru na piramidę trójkątną

Pytanie 1. Biorąc pod uwagę trójkątną piramidę o polu podstawy 15 jednostek kwadratowych i wysokości 10 jednostek, jaka jest objętość piramidy?

Pytanie 2. Biorąc pod uwagę regularną trójkątną piramidę, której każda krawędź podstawy trójkąta równobocznego ma 6 jednostek, jakie jest całkowite pole powierzchni piramidy?

Pytanie 3. Biorąc pod uwagę regularną trójkątną piramidę, której każda krawędź podstawy trójkąta równobocznego ma wymiary 4 jednostki i wysokość 5 jednostek, jaka jest objętość i całkowite pole powierzchni piramidy?

Pytanie 4. Jeśli długości boków podstawy trójkątnej piramidy wynoszą 3 jednostki, 4 jednostki i 5 jednostek, a wysokość piramidy wynosi 12 jednostek, jaka jest objętość piramidy?

Pytanie 5. Jakie jest pole powierzchni piramidy trójkątnej o podstawie w kształcie trójkąta prostokątnego z nogami o długości 3 i 4 jednostek oraz przeciwprostokątną o długości 5 jednostek, jeśli wysokość ostrosłupa od podstawy do wierzchołka wynosi 10 jednostek ?

Często zadawane pytania dotyczące wzoru na piramidę trójkątną

Jaka jest definicja trójkątnej piramidy?

Trójkątna piramida to geometryczny kształt, który ma trójkątną podstawę i trzy trójkątne ściany mające wspólny wierzchołek.

Ile ścian i wierzchołków ma piramida trójkątna?

Trójkątna piramida ma cztery ściany i cztery wierzchołki. Jeden wierzchołek jest wspólny dla wszystkich trzech ścian piramidy.

Jaki jest podstawowy wzór na piramidę?

Podstawowe wzory piramidy to:

• LSA = ½ × obwód × wysokość nachylenia
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Jakie są rodzaje piramid trójkątnych?

Istnieją trzy rodzaje piramid trójkątnych

• Regularna trójkątna piramida
• Nieregularna trójkątna piramida
• Piramida trójkątna prostokątna

Jaki jest wzór na trójkąty?

Wzór na pole trójkąta to:

• (Powierzchnia)A = 1/2 × b × h