W tym artykule omówimy przechodzenie przez drzewo w strukturze danych. Termin „przechodzenie przez drzewo” oznacza przechodzenie lub odwiedzanie każdego węzła drzewa. Istnieje jeden sposób poruszania się po liniowej strukturze danych, takiej jak lista połączona, kolejka i stos. Istnieje wiele sposobów przemierzania drzewa, które wymieniono poniżej:
- Przejście w przedsprzedaży
- Przeprawa nieuporządkowana
- Przebieg przekazu pocztowego
Dlatego w tym artykule omówimy wyżej wymienione techniki przechodzenia przez drzewo. Zacznijmy teraz omawiać sposoby poruszania się po drzewach.
Przejście w przedsprzedaży
Ta technika jest zgodna z polityką „root lewy prawy”. Oznacza to, że odwiedzany jest pierwszy węzeł główny, po którym następuje rekurencyjne przechodzenie przez lewe poddrzewo, a na koniec rekursywne przechodzenie przez prawe poddrzewo. Ponieważ węzeł główny jest przemierzany przed (lub przed) lewym i prawym poddrzewem, nazywa się to przechodzeniem w przedsprzedaży.
Zatem w przypadku przeglądania w przedsprzedaży każdy węzeł jest odwiedzany przed obydwoma jego poddrzewami.
Zastosowania przechodzenia w przedsprzedaży obejmują:
- Służy do tworzenia kopii drzewa.
- Można go również użyć do uzyskania wyrażenia przedrostkowego drzewa wyrażeń.
Algorytm
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Przykład
Zobaczmy teraz przykład techniki przeglądania w przedsprzedaży.
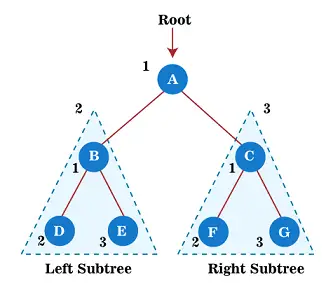
Teraz zacznij stosować przechodzenie w przedsprzedaży na powyższym drzewie. Najpierw przechodzimy przez węzeł główny A; następnie przejdź do lewego poddrzewa B , który będzie również dostępny w przedsprzedaży.
Zatem w przypadku lewego poddrzewa B najpierw węzeł główny B sam jest przemierzany; potem jego lewe poddrzewo D jest przekroczony. Ponieważ węzeł D nie ma żadnych dzieci, przejdź do prawego poddrzewa I . Ponieważ węzeł E również nie ma żadnych dzieci, przechodzenie przez lewe poddrzewo węzła głównego A jest zakończone.
Nowa linia Pythona
Teraz przejdź w kierunku prawego poddrzewa węzła głównego A, czyli C. Zatem w przypadku prawego poddrzewa C najpierw węzeł główny C przeszedł sam siebie; potem jego lewe poddrzewo F jest przekroczony. Ponieważ węzeł F nie ma żadnych dzieci, przejdź do prawego poddrzewa G . Ponieważ węzeł G również nie ma żadnych dzieci, przechodzenie przez prawe poddrzewo węzła głównego A jest zakończone.
Dlatego przechodzą wszystkie węzły drzewa. Zatem wynik przejścia powyższego drzewa w przedsprzedaży wynosi -
A → B → D → E → C → F → G
Aby dowiedzieć się więcej na temat przeglądania przedsprzedaży w strukturze danych, możesz skorzystać z linku Przejście w przedsprzedaży .
Przebieg przekazu pocztowego
Ta technika jest zgodna z zasadą „lewy-prawy root”. Oznacza to, że przechodzi się przez pierwsze lewe poddrzewo węzła głównego, następnie rekurencyjnie przechodzi przez prawe poddrzewo i na koniec przechodzi się przez węzeł główny. Ponieważ węzeł główny jest przemierzany po (lub po) lewym i prawym poddrzewie, nazywa się to przechodzeniem po zamówieniu.
Zatem w przypadku przeglądania postorder każdy węzeł jest odwiedzany po obu jego poddrzewach.
Zastosowania postorder traversal obejmują:
- Służy do usuwania drzewa.
- Można go również użyć do uzyskania wyrażenia przyrostkowego drzewa wyrażeń.
Algorytm
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Przykład
Domyślne parametry Javy
Zobaczmy teraz przykład techniki przechodzenia po zamówieniu.

Teraz zacznij stosować przechodzenie postorder na powyższym drzewie. Najpierw przemierzamy lewe poddrzewo B, które będzie przechodzić w kolejności post-order. Następnie będziemy przechodzić przez prawe poddrzewo C w wysyłce. I wreszcie węzeł główny powyższego drzewa, tj. A , zostaje przekroczony.
Zatem dla lewego poddrzewa B najpierw jego lewe poddrzewo D jest przekroczony. Ponieważ węzeł D nie ma żadnych dzieci, przejdź do prawego poddrzewa I . Ponieważ węzeł E również nie ma żadnych dzieci, przejdź do węzła głównego B. Po przejściu węzła B, przechodzenie przez lewe poddrzewo węzła głównego A zostało zakończone.
wybierz jako
Teraz przejdź w kierunku prawego poddrzewa węzła głównego A, czyli C. Zatem w przypadku prawego poddrzewa C najpierw jego lewe poddrzewo F jest przekroczony. Ponieważ węzeł F nie ma żadnych dzieci, przejdź do prawego poddrzewa G . Ponieważ węzeł G również nie ma dzieci, dlatego ostatecznie węzeł główny prawego poddrzewa, tj. C, jest przekroczony. Zakończono przechodzenie przez prawe poddrzewo węzła głównego A.
Na koniec przejdź przez węzeł główny danego drzewa, tj. A . Po przejściu przez węzeł główny następuje zakończenie postorderowego przejścia danego drzewa.
Dlatego przechodzą wszystkie węzły drzewa. Zatem wynikiem postorderowego przejścia powyższego drzewa jest -
D → E → B → F → G → C → A
Aby dowiedzieć się więcej o przechodzeniu postordera w strukturze danych, możesz skorzystać z linku Przebieg przekazu pocztowego .
Przeprawa nieuporządkowana
Ta technika jest zgodna z polityką „lewego głównego prawego”. Oznacza to, że po przejściu węzła głównego odwiedzane jest pierwsze lewe poddrzewo, a na koniec odwiedzane jest prawe poddrzewo. Ponieważ węzeł główny przechodzi pomiędzy lewym i prawym poddrzewem, nazywa się to przechodzeniem w kolejności.
Zatem podczas przechodzenia w kolejności każdy węzeł jest odwiedzany pomiędzy jego poddrzewami.
Zastosowania przejścia Inorder obejmują -
- Służy do uporządkowania węzłów BST w kolejności rosnącej.
- Można go również użyć do uzyskania wyrażenia przedrostkowego drzewa wyrażeń.
Algorytm
przykładowy kod w języku c#
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Przykład
Zobaczmy teraz przykład techniki przemierzania Inorder.

Teraz zacznij stosować przejście wewnętrzne na powyższym drzewie. Najpierw przemierzamy lewe poddrzewo B które zostaną przebyte w kolejności. Następnie przejdziemy przez węzeł główny A . I wreszcie prawe poddrzewo C jest przemierzany w kolejności.
Zatem dla lewego poddrzewa B po pierwsze, jego lewe poddrzewo D jest przekroczony. Ponieważ węzeł D nie ma żadnych dzieci, więc po przejściu przez niego node B zostanie przebyte i w końcu prawe poddrzewo węzła B I , zostaje przekroczony. Węzeł E również nie ma żadnych dzieci; w związku z tym przechodzenie przez lewe poddrzewo węzła głównego A jest zakończone.
Następnie przechodzimy przez węzeł główny danego drzewa, tj. A .
Na koniec przejdź w kierunku prawego poddrzewa węzła głównego A, czyli C. Zatem dla prawego poddrzewa C; po pierwsze, jego lewe poddrzewo F jest przekroczony. Ponieważ węzeł F nie ma dzieci, node C zostanie przebyte i w końcu prawe poddrzewo węzła C, czyli G , zostaje przekroczony. Węzeł G również nie ma żadnych dzieci; w związku z tym przechodzenie przez prawe poddrzewo węzła głównego A jest zakończone.
Gdy wszystkie węzły drzewa zostaną przebyte, przechodzenie wewnętrzne danego drzewa zostaje zakończone. Wynikiem przejścia wewnętrznego powyższego drzewa jest -
D → B → E → A → F → C → G
Aby dowiedzieć się więcej na temat przechodzenia w kolejności wewnętrznej w strukturze danych, możesz skorzystać z linku Przeprawa nieuporządkowana .
Złożoność technik przechodzenia przez drzewa
Omówiona powyżej złożoność czasowa technik przechodzenia przez drzewa wynosi NA) , Gdzie 'N' jest rozmiarem drzewa binarnego.
Natomiast złożoność przestrzenna technik przechodzenia przez drzewa omówionych powyżej wynosi O(1) jeśli nie weźmiemy pod uwagę rozmiaru stosu dla wywołań funkcji. W przeciwnym razie złożoność przestrzenna tych technik wynosi Oh) , Gdzie 'H' to wysokość drzewa.
Implementacja przechodzenia przez drzewo
Przyjrzyjmy się teraz implementacji omówionych powyżej technik przy użyciu różnych języków programowania.
Program: Napisz program implementujący techniki przechodzenia przez drzewo w języku C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Wyjście

Program: Napisz program implementujący techniki przechodzenia przez drzewo w języku C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Wyjście

Program: Napisz program implementujący techniki przechodzenia przez drzewo w języku C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Wyjście
Po wykonaniu powyższego kodu wyjściem będzie -
a b c liczby

Wniosek
W tym artykule omówiliśmy różne typy technik przechodzenia przez drzewo: przechodzenie przed porządkiem, przechodzenie w kolejności i przechodzenie po zamówieniu. Widzieliśmy te techniki wraz z algorytmem, przykładem, złożonością i implementacją w językach C, C++, C# i Java.
To tyle na temat artykułu. Mam nadzieję, że będzie dla Ciebie pomocny i pouczający.
