Koder to obwód cyfrowy, który przekształca zestaw wejść binarnych na unikalny kod binarny. Kod binarny reprezentuje pozycję wejścia i służy do identyfikacji konkretnego wejścia, które jest aktywne. Enkodery są powszechnie używane w systemach cyfrowych do konwersji równoległego zestawu wejść na kod szeregowy.
Podstawową zasadą działania enkodera jest przypisanie każdemu możliwemu wejściu unikalnego kodu binarnego. Na przykład koder 2 do 4 linii ma 2 linie wejściowe i 4 linie wyjściowe i przypisuje unikalny 4-bitowy kod binarny do każdej z 2^2 = 4 możliwych kombinacji wejściowych. Wyjście enkodera jest zwykle aktywne w stanie niskim, co oznacza, że w danym momencie tylko jedno wyjście jest aktywne (niskie), a pozostałe wyjścia są nieaktywne (wysokie). Aktywne wyjście niskie jest wybierane na podstawie kodu binarnego przypisanego do aktywnego wejścia.
połączona lista Java
Istnieją różne typy enkoderów, w tym enkodery priorytetowe, które przypisują priorytet każdemu wejściu, oraz enkodery ważone binarnie, które wykorzystują binarny system ważenia do przypisywania kodów binarnych do wejść. Podsumowując, enkoder to obwód cyfrowy, który przekształca zestaw wejść binarnych na unikalny kod binarny reprezentujący położenie wejścia. Enkodery są szeroko stosowane w systemach cyfrowych do konwersji wejść równoległych na kody szeregowe.
Koder to obwód kombinacyjny który wykonuje operację odwrotną do a Dekoder . Ma maksymalnie 2^n linii wejściowych I „n” linii wyjściowych , stąd koduje informacje z 2^n wejść w n-bitowy kod. Wygeneruje kod binarny odpowiadający wejściu, które jest aktywne Wysokie. Dlatego koder koduje 2^n linii wejściowych za pomocą „n” bitów.
Koder
Rodzaje enkoderów
Istnieją różne typy koderów, które są wymienione poniżej.
- Koder 4 do 2
- Koder ósemkowy na binarny (enkoder 8 na 3)
- Koder dziesiętny na BCD
- Koder priorytetowy
Koder 4 do 2
Enkoder 4 do 2 składa się z cztery wejścia Y3, Y2, Y1 i Y0 oraz dwa wyjścia A1 i A0 . W dowolnym momencie tylko jedno z tych 4 wejść może mieć wartość „1”, aby uzyskać odpowiedni kod binarny na wyjściu. Poniższy rysunek przedstawia symbol logiczny enkodera 4 do 2.
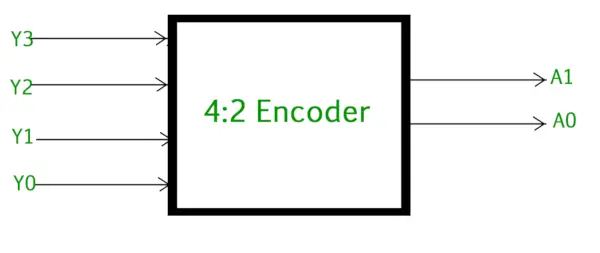
Koder 4 do 2
Tabela prawdy dla 4 do 2 koderów jest następująca.
| WEJŚCIA | WYJŚCIA | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Wyrażenie logiczne dla A1 i A0:
A1 = Y3 + Y2 A0 = Y3 + Y1>
Powyższe dwie funkcje logiczne A1 i A0 można zaimplementować przy użyciu dwóch wejściowych bramek OR:
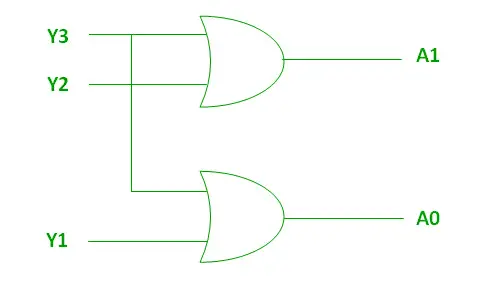
Implementacja z wykorzystaniem bramki OR
Koder ósemkowy na binarny (enkoder 8 na 3)
Koder 8 do 3 lub koder ósemkowy na binarny składa się z 8 wejść : Y7 do Y0 i 3 wyjścia : A2, A1 i A0. Każda linia wejściowa odpowiada każdej cyfrze ósemkowej, a trzy wyjścia generują odpowiedni kod binarny. Poniższy rysunek przedstawia symbol logiczny ósemkowy do enkodera binarnego.
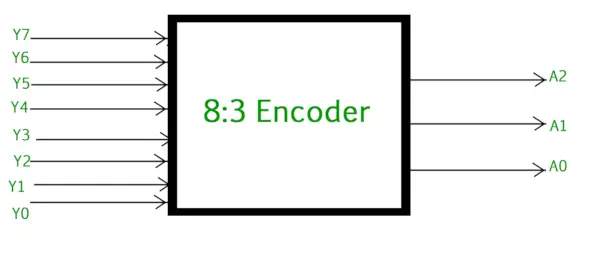
Koder ósemkowy na binarny (enkoder 8 na 3)
Tabela prawdy dla kodera 8 do 3 jest następująca.
| WEJŚCIA | WYJŚCIA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Wyrażenie logiczne dla A2, A1 i A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Powyższe dwie funkcje logiczne A2, A1 i A0 można zaimplementować przy użyciu czterech wejść LUB bramy .
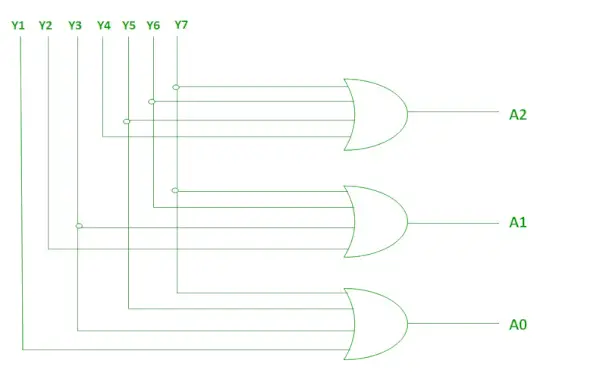
Implementacja z wykorzystaniem bramki OR
Koder dziesiętny na BCD
Koder dziesiętny-binarny zwykle składa się z 10 linii wejściowych I 4 linie wyjściowe . Każda linia wejściowa odpowiada każdej cyfrze dziesiętnej, a 4 wyjścia odpowiadają kodowi BCD. Ten koder przyjmuje zdekodowane dane dziesiętne jako dane wejściowe i koduje je na wyjściu BCD, które jest dostępne na liniach wyjściowych. Poniższy rysunek przedstawia symbol logiczny kodera dziesiętnego na BCD:
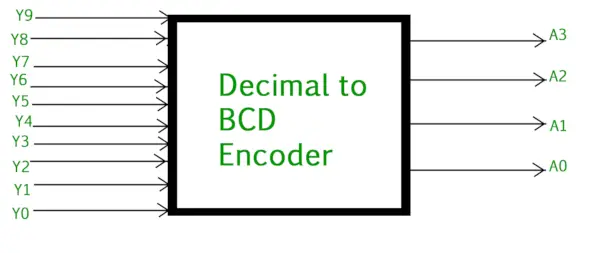
Koder dziesiętny na BCD
Tabela prawdy dla dziesiętnych do Koder BCD następująco.
| WEJŚCIA | WYJŚCIA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Wyrażenie logiczne dla A3, A2, A1 i A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Powyższe dwie funkcje logiczne można zaimplementować za pomocą bramek OR.
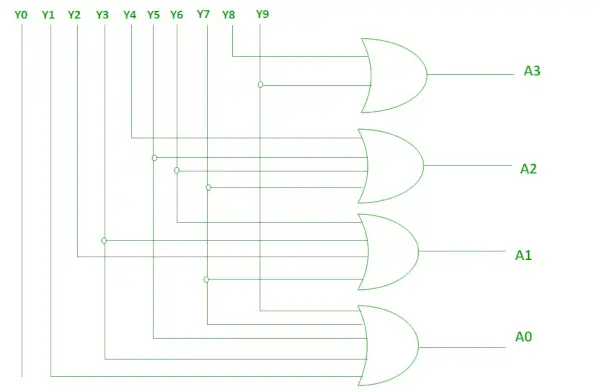
Implementacja z wykorzystaniem bramki OR
Koder priorytetowy
Koder priorytetowy 4 do 2 ma 4 wejścia : Y3, Y2, Y1 i Y0 oraz 2 wyjścia : A1 i A0. Tutaj wejście Y3 ma najwyższy priorytet , podczas gdy wejście Y0 ma najniższy priorytet . W tym przypadku, nawet jeśli więcej niż jedno wejście ma jednocześnie wartość „1”, na wyjściu będzie kod (binarny) odpowiadający wejściu, które ma wyższy priorytet . Tabela prawdy dla kodera priorytetowego jest następująca.
| WEJŚCIA | WYJŚCIA | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | W |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
Poniżej pokazano wyrażenie logiczne dla A1.
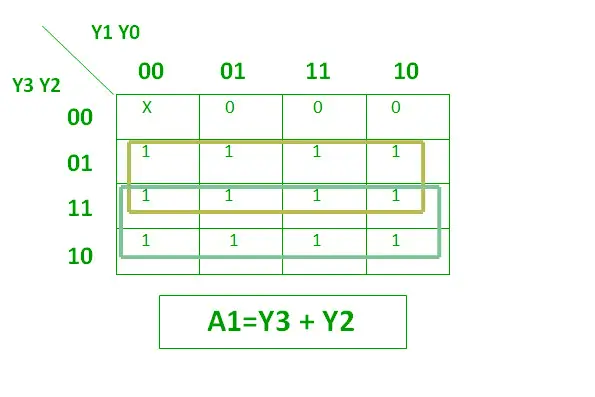
Wyrażenie logiczne
Poniżej pokazano wyrażenie logiczne dla A0.
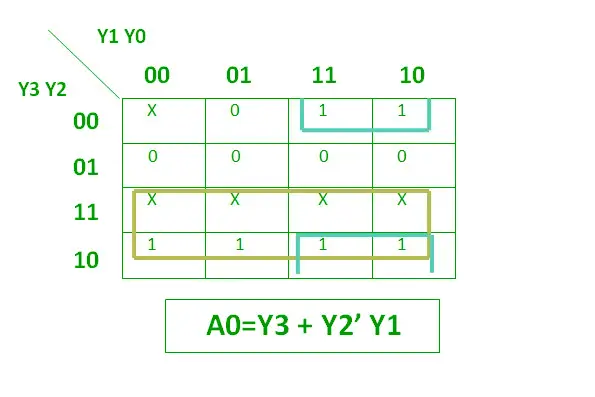
Wyrażenie logiczne
Powyższe dwie funkcje logiczne można zaimplementować jako.
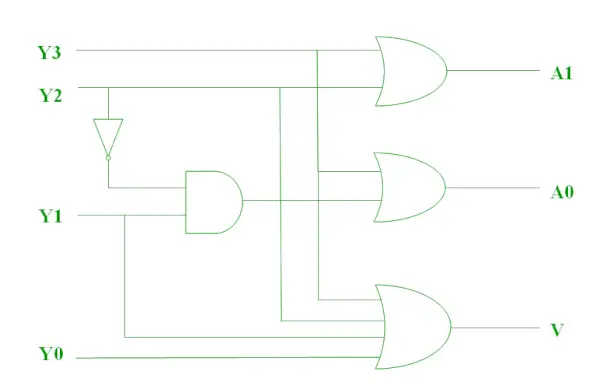
Koder priorytetowy
Poniżej wymieniono pewne błędy, które zwykle występują w koderach.
- Niejednoznaczność występuje, gdy wszystkie wyjścia enkodera są równe zeru.
- Jeśli więcej niż jedno wejście jest aktywne w stanie wysokim, koder generuje sygnał wyjściowy, który może nie być prawidłowym kodem.
Aby więc przezwyciężyć te trudności, powinniśmy przypisać priorytety każdemu wejściu kodera. Wówczas wyjściem enkodera będzie kod odpowiadający aktywnym wysokim wejściom, które mają wyższy priorytet.
Zastosowanie enkoderów
- Enkodery to bardzo popularne obwody elektroniczne stosowane we wszystkich systemach cyfrowych.
- Enkodery służą do tłumaczenia wartości dziesiętnych na binarne w celu wykonywania funkcji binarnych, takich jak dodawanie, odejmowanie, mnożenie itp.
- Inne zastosowania, zwłaszcza dla enkoderów priorytetowych, mogą obejmować wykrywanie przerwań w aplikacjach mikroprocesorowych.
Zalety stosowania koderów w logice cyfrowej
- Zmniejszenie liczby linii: Enkodery zmniejszają liczbę linii wymaganych do przesłania informacji z wielu wejść do jednego wyjścia, co może uprościć konstrukcję systemu i obniżyć koszt komponentów.
- Poprawiona niezawodność: Konwertując wiele wejść na jeden kod seryjny, kodery mogą zmniejszyć ryzyko błędów w transmisji informacji.
- Poprawiona wydajność: Kodery mogą zwiększyć wydajność systemu cyfrowego, skracając czas wymagany do przesłania informacji z wielu wejść do jednego wyjścia.
Wady stosowania koderów w logice cyfrowej
- Zwiększona złożoność: Enkodery są zazwyczaj bardziej złożonymi obwodami w porównaniu do multipleksery i wymagają dodatkowych komponentów do wdrożenia.
- Ograniczone do określonych zastosowań: Enkodery nadają się tylko do zastosowań, w których równoległy zestaw wejść musi zostać przekonwertowany na kod szeregowy.
- Ograniczona elastyczność: Enkodery mają ograniczoną elastyczność, ponieważ mogą zakodować tylko stałą liczbę wejść w ustalonej liczbie wyjść.
- Podsumowując, enkodery to przydatne obwody cyfrowe, które mają swoje zalety i wady. Decyzja o zastosowaniu enkodera zależy od konkretnych wymagań systemu i kompromisów pomiędzy złożonością, niezawodnością, wydajnością i kosztem.
Pytania narożne GATE CS
Przećwiczenie poniższych pytań pomoże Ci sprawdzić swoją wiedzę. Wszystkie pytania zostały zadane w GATE w poprzednich latach lub w GATE Mock Tests. Zdecydowanie zaleca się ich przećwiczenie.
- GATE CS 2013, pytanie 65
- GATE CS 2014 (zestaw 3), pytanie 65
