Linie poziome definiuje się jako linie równoległe do horyzontu lub ziemi, stąd nazwa linia pozioma . Linia pozioma ma zerowe nachylenie, czyli kąt nachylenia tych linii wynosi zero stopni. Jeśli linie poziome są rysowane na płaszczyznach kartezjańskich, przecinają się one tylko wzdłuż osi y, ponieważ są zawsze równoległe do osi x i nigdy jej nie przecinają.
W tym artykule dowiemy się o linii poziomej, jej właściwościach, nachyleniu linii poziomej, równaniu linii poziomej, przykładach i często zadawanych pytaniach związanych z liniami poziomymi i innych szczegółowo.
skaner w Javie
Spis treści
- Definicja linii poziomej
- Nachylenie linii poziomej
- Rysowanie linii poziomej
- Równanie linii poziomej
- Test linii poziomej
- Linie poziome i pionowe
- Różnice między liniami pionowymi i poziomymi
- Krótka uwaga na temat linii poziomej
- Przykłady linii poziomych
Definicja linii poziomej
Wiemy, że linia to prosta droga, która łączy dwa lub więcej dwa punkty i biegnie do nieskończoności. Zatem linie poziome definiujemy jako linie równoległe do podłoża lub horyzontu i znajdujące się na stałej wysokości od podłoża.
Jeśli narysujemy te proste w układzie kartezjańskim, to będą to proste, które nie mają punktu przecięcia na osi x, ale mają punkt przecięcia na osi y. Linie poziome mają zerowe nachylenie, czyli mają zerowy kąt z osią x lub z podłożem.
Poziome linie tworzą podstawę różnych obiektów, kształtów i figur, które badamy w geometrii. Załóżmy, że musimy narysować prostokąt, kwadrat, trójkąt, trapez itp., wówczas podstawą tych figur są głównie linie poziome. W prawdziwym życiu obserwujemy również kłamstwa poziome, ponieważ linie na podłodze i dachu pomieszczeń, podstawa schodów itp. również są tworzone przez linie poziome.
Liny te nazywane są również linkami do spania, ponieważ nie poruszają się w pionie i zawsze pozostają na stałej wysokości nad ziemią. Obraz dodany poniżej przedstawia linię poziomą.
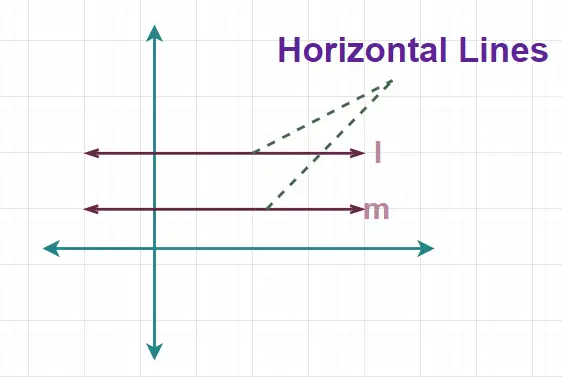
Tutaj, na rysunku dodanym powyżej, linie l i m są liniami poziomymi.
Nachylenie linii poziomej
Wspomnieliśmy już, że nachylenie linii poziomej wynosi zero . Teraz nauczmy się, jak nachylenie linii poziomej wynosi zero. Obliczamy nachylenie linii poziomej, korzystając ze wzoru:
Nachylenie = wzrost/bieg
LUB
Nachylenie linii = zmiana współrzędnej y/zmiana współrzędnej x
Gdzie Rise to wysokość, jaką uzyska linia biegnąc od lewej do prawej, ponieważ wiemy już, że linia pozioma jest równoległa do osi x i zawsze ma stałą wysokość, zatem mówimy, że te linie mają zerowy wznios, więc nachylenie tych linii wynosi,
Zatem nachylenie = 0/bieg = 0
Stwierdza się zatem, że nachylenie linii poziomej wynosi zero.
Rysowanie linii poziomej
Linie poziome można łatwo narysować, korzystając z kroków omówionych poniżej,
Krok 1: Wybierz punkt na płaszczyźnie kartezjańskiej, dla którego musimy znaleźć linię poziomą. Załóżmy, że punktem jest (1, 2)
Krok 2: Zaznacza współrzędną y punktu. W tym przypadku współrzędna y wynosi 2.
Krok 3: Zaznacz inne punkty, których współrzędna y jest taka sama jak punkt w kroku 1. Niech pozostałe punkty to (-2, 2), (0, 2) i (7, 2)
Krok 4: Połącz wszystkie punkty, aby uzyskać odcinek linii i rozciągnij je po obu stronach, aby uzyskać linię poziomą.
Jest to wymagana linia pozioma przechodząca przez punkt (1, 2) i ma nachylenie zerowe.

Równanie linii poziomej
Wiemy, że równanie prostej w układzie współrzędnych 2-D wygląda następująco:
y = mx + do
Gdzie,
- m jest nachyleniem linii
- c jest punktem przecięcia z osią y
Wiemy, że dla linii poziomej nachylenie wynosi zero. Podstawiając tę wartość do powyższego równania otrzymujemy równanie linii poziomej:
jak wyłączyć tryb programisty na Androidzie
y = 0x + do
y = do
Gdzie C jest stałą.
Zatem powyższe równanie y = c jest równaniem linii poziomej.
Równanie to oznacza, że linia pozioma to linia przechodząca przez wszystkie punkty układu kartezjańskiego, w których współrzędna y jest równa „c”. To przecięcie linii nie ma współrzędnej x, a zatem linia ta nigdy nie przecina osi x, a przecina oś y w punkcie (0, c).
Można zatem powiedzieć, że równanie prostej poziomej wynosi y = c(stała) i przechodzi ona przez punkt (a, c), w którym a może przyjmować dowolną wartość, a c jest zawsze stałe.
Test linii poziomej
Testem używanym do określenia, czy funkcja jest funkcją jeden do jednego, czy nie, jest test linii poziomej. W teście linii poziomej rysujemy linię poziomą przechodzącą przez dowolny punkt funkcji i jeśli linie przecinają funkcję w jakimkolwiek innym punkcie, to funkcja NIE jest funkcją jeden do jednego. Zatem, aby funkcja była jednoznaczna, musi przejść test linii poziomej, tj. każda linia pozioma musi przeciąć funkcję tylko raz.
Wiemy, że funkcje jeden do jednego to funkcje, w których dla każdej wartości x mamy tylko jedną wartość y. Zatem, jeśli linia pozioma przechodzi przez funkcję i przecina ją tylko raz, to możemy powiedzieć, że dla unikalnej wartości y mamy unikalną wartość x. Ale jeśli linia pozioma przecina funkcję więcej niż raz, otrzymamy dwie wartości dla unikalnej wartości y, co nie ma miejsca w przypadku funkcji jeden do jednego.
Test linii poziomej pomaga nam określić, czy funkcja jest funkcją jeden-jeden. Można to zrozumieć za pomocą obrazu dodanego poniżej.

Na pierwszym obrazie funkcja jest jednoznaczna, ponieważ linia pozioma przechodzi tylko przez jeden punkt funkcji.
Na drugim obrazie funkcja NIE jest różnowartościowa, ponieważ linia pozioma przechodzi przez więcej niż jeden punkt funkcji.
Linie poziome i pionowe
Linie poziome to linie równoległe do podłoża lub horyzontu. Linie te nazywane są również liniami sypialnymi. W systemie kartezjańskim linie te są równoległe do osi x, natomiast w przypadku linii pionowych są to linie prostopadłe do linii poziomych i nazywane są liniami stojącymi. i są równoległe do osi y w układzie kartezjańskim.
Linie poziome to linie biegnące od lewej do prawej w systemie kartezjańskim, natomiast linie pionowe to linie biegnące w górę i w dół w systemie kartezjańskim.
Linie pionowe i poziome są do siebie prostopadłe. Obraz dodany poniżej przedstawia linię pionową i poziomą.

Różnice między liniami pionowymi i poziomymi
Różnice między liniami pionowymi i poziomymi można łatwo zrozumieć, analizując tabelę dodaną poniżej.
| Linia pozioma | Pionowa linia |
|---|---|
| Linie te są równoległe do ziemi lub horyzontu. | Te linie są prostopadły do ziemi lub horyzontu. |
| Nachylenie linii poziomej wynosi zero. | Nachylenie linii pionowej jest nieokreślone. |
| Linia pozioma tworzyła z horyzontem kąt zerowy. | Linia pionowa tworzyła z horyzontem kąt 90 stopni. |
| Równanie poziomej linii przechodzącej przez punkt (h, k) to: y = k | Równanie linii pionowej przechodzącej przez punkt (h, k) to: x = godz |
| Linie poziome są równoległe do osi x w układzie kartezjańskim. | Linie pionowe są równoległe do osi y w układzie kartezjańskim. |
| Przykładami reprezentującymi linie poziome są:
| Przykładami reprezentującymi linie pionowe są:
|
Krótka uwaga na temat linii poziomej
Linia pozioma w matematyce jest idealnie płaska, równoległa do horyzontu. Biegnie od lewej do prawej i ma nachylenie 0. W geometrii jest przedstawiane jako linia prosta łącząca dowolne dwa punkty na tej samej wysokości na płaszczyźnie. Równanie linii poziomej ma postać (y = k), gdzie (k) jest stałą wartością reprezentującą wysokość linii na osi y.
Czytaj więcej:
- Rodzaje linii
- Równoległe linie
- Jak dodać poziomą linię w HTML?
- Jak używać pełnej poziomej przestrzeni linii w HTML?
- Jak rysować linie poziome i pionowe w aplikacji na Androida przy użyciu XML
Przykłady linii poziomych
Przykład 1: Znajdź równanie prostej poziomej przechodzącej przez punkt (1, -1).
Rozwiązanie:
Wiemy, że nachylenie linii poziomej wynosi m = 0.
Dany punkt (1, -1)
Równanie prostej przechodzącej przez punkt (x1, I1) i mający nachylenie (m) wynosi,
i i1= m(x – x1)
Podstawiając wartości w powyższym równaniu otrzymujemy,
y – (-1) = 0(x – 1)
i + 1 = 0
y = -1
Zatem równanie prostej poziomej przechodzącej przez punkt (1, -1) wynosi y = -1
Przykład 2: Znajdź równanie prostej poziomej przechodzącej przez punkt (5, 9).
Rozwiązanie:
Wiemy, że nachylenie linii poziomej wynosi m = 0.
ciąg długościDany punkt (5, 9)
Równanie prostej przechodzącej przez punkt (x1, I1) i mający nachylenie (m) wynosi,
i i1= m(x – x1)
Podstawiając wartości w powyższym równaniu otrzymujemy,
y – (9) = 0(x – 5)
i – 9 = 0
y = 9
Zatem równanie prostej poziomej przechodzącej przez punkt (5, 9) wynosi y = 9
Przykład 3: Znajdź równanie linii poziomej, gdy punkt przecięcia z osią y wynosi 5.
Rozwiązanie:
Równanie linii poziomej to:
y = k
Gdzie k jest punktem przecięcia z Y
kody kolorów JavaDany
- k = 5
Równanie linii poziomej,
y = 5
Zatem równanie pozioma linia z punktem przecięcia y wynoszącym 5 wynosi: y = 5
Przykład 4: Znajdź równanie linii poziomej, gdy punkt przecięcia z osią y wynosi -11/3.
Rozwiązanie:
Równanie linii poziomej to:
y = k
Gdzie k jest punktem przecięcia z Y
Dany
- k = -11/3
Równanie linii poziomej,
y = -11/3
3 lata = -11
3 lata + 11 = 0
Zatem pozioma linia równania z punktem przecięcia y wynoszącym -11/3 wynosi: 3y + 11 = 0
Linie poziome – często zadawane pytania
Co to są linie poziome?
Linie poziome to linie równoległe do horyzontu lub ziemi. W układzie kartezjańskim linie poziome są równoległe do osi x.
Jakie jest równanie linii poziomej?
Równanie linii poziomej to:
y = k
Gdzie k jest punktem przecięcia na osi y.
Jakie jest nachylenie linii poziomej?
Nachylenie linii poziomej jest zawsze równe zeru, ponieważ tworzą one kąt zerowy z osią x.
Jakie są przykłady linii poziomych?
Przykładami reprezentującymi linie poziome są:
- Prosta droga
- Dół schodów
- Podstawa dowolnej figury itp.
Jak nazywają się poziome linie na kuli ziemskiej?
Poziome linie biegnące po kuli ziemskiej nazywane są szerokościami geograficznymi i biegną równolegle do równika.
Jakie są właściwości linii poziomych?
Różne właściwości linii poziomych to:
- Są równoległe do podłoża, horyzontu i osi X.
- Są prostopadłe do osi Y.
- Nachylenie linii poziomej wynosi zero itp.
Która linia jest pionowa, a która pozioma?
Linia pionowa jest równoległa do osi y i biegnie prosto w górę i w dół w płaszczyźnie współrzędnych, natomiast linia pozioma jest równoległa do osi x i biegnie prosto w lewo i prawo.
Jakie jest nachylenie linii poziomej i pionowej?
Nachylenie linii wskazuje na jej stromość i kierunek. Oblicza się ją jako stosunek zmiany pionowej do zmiany poziomej pomiędzy dwoma punktami na linii.
Jakie są poziome i pionowe linie punktowe?
Linie poziome rozciągają się od lewej do prawej lub od prawej do lewej i biegną równolegle do osi x, podczas gdy linie pionowe rozciągają się w górę i w dół oraz biegną równolegle do osi y. Te dwa typy linii są do siebie prostopadłe.
