Środek trójkąta jest punktem przecięcia wszystkich trzech dwusiecznych kątów trójkąta. Środek jest ważnym punktem trójkąta, w którym spotykają się linie przecinające kąty na pół. Ten punkt jest także środkiem okręgu zwanego Incircle, który idealnie pasuje do trójkąta i tak samo dotyka wszystkich trzech boków. W tym artykule omówiono różne koncepcje środka trójkąta, na przykład dlaczego ten punkt jest ważny, jak go znaleźć za pomocą kompasu lub liczb oraz właściwości środka koła.

Spis treści

• Co to jest środek trójkąta?
• Właściwości środka trójkąta
• Środek wzoru na trójkąt
• Jak znaleźć środek trójkąta
• Środek ciężkości, środek okręgu, środek wtrącony, ortocentrum

Co to jest środek trójkąta?

Środek trójkąta, jak sama nazwa wskazuje, jest punktem środkowym trójkąta. Ten punkt, który nazywamy środkiem, tworzy się na skrzyżowaniu, gdzie spotykają się wszystkie linie przecinające kąty wewnętrzne. Odległość punktu od wszystkich trzech boków trójkąta jest taka sama. Okrąg trójkąta pasuje również do idealnego okręgu wewnątrz trójkąta i okrąg ten nazywany jest okręgiem wpisanym w trójkąt.

Definicja centrum

Środek trójkąta to punkt wewnątrz trójkąta, w którym zbiegają się wszystkie trzy linie przecinające jego kąty wewnętrzne na pół. Punkt ten znajduje się w tej samej odległości od trzech boków trójkąta, co czyni go środkiem trójkąta. Jest to także środek największego okręgu, który mieści się w trójkącie, który nazywamy okręgiem wpisanym. Aby symbolizować środek, zwykle używamy litery I,

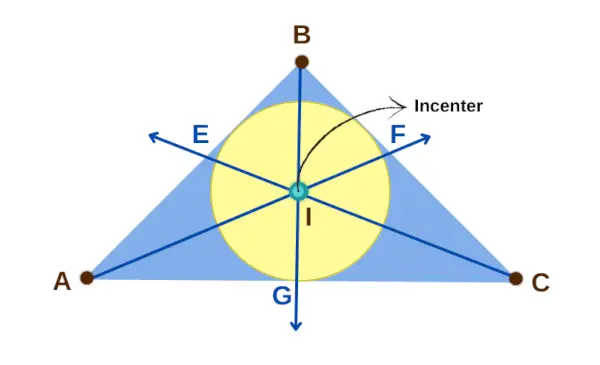
Środek trójkąta

Właściwości środka trójkąta

Poniżej podano kilka ważnych właściwości środka trójkąta:

Właściwość 1: Jeśli I jest środkiem trójkąta ABC, to trzy pary odcinków są równej długości: AE i AG, CG i CF oraz BF i BE. Oznacza to, że AE = AG, CG = CF i BF = BE.

Właściwość 2: Centrum I ma również szczególny związek z kątami trójkąta. Powoduje to, że kąty ∠BAI i ∠CAI są równe, ∠BCI i ∠ACI są równe, a ∠ABI i ∠CBI są równe. Jest to zgodne z twierdzeniem o dwusiecznej kąta.

Właściwość 3: Centrum I jest środkiem okręgu, który dotyka wszystkich trzech boków trójkąta, i odległościami od I do boków trójkąta (EI, FI, GI) są takie same. Odległości te nazywane są inradii lub promieniem okręgu.

Właściwość 4: Możesz obliczyć pole trójkąta, korzystając z półobwodu (s) i promienia (r). Wzór jest następujący: A = sr, gdzie A to pole, s to półobwód (s = (a + b + c)/2, gdzie a, b i c to długości boków trójkąta), a r to promień.

Właściwość 5: Środek trójkąta zawsze pozostaje wewnątrz trójkąta. W przeciwieństwie do ortocentrum, które w niektórych przypadkach może znajdować się na zewnątrz trójkąta, incenter zawsze mieści się w granicach trójkąta.

Środek wzoru na trójkąt

Wzór na znalezienie środka wzoru z 3 współrzędnymi (x₁, I₁), (X₂, I₂) i (x₃, I₃) Jest:

{(topór ₁ + bx ₂ + cx ₃ )/(a + b + c), (jest ₁ + przez ₂ + c ₃ )/(a + b + c)}

Mówiąc najprościej, aby uzyskać incenter, należy:

• Pomnóż współrzędną x punktu A przez długość boku a, współrzędną x punktu B przez długość boku b i współrzędną x punktu C przez długość boku c. Następnie dodaj je razem.
• Wynik podziel przez sumę długości boków a, b i c.
• Powtórz ten sam proces dla współrzędnych y, ale używając długości boków a, b i c.

Środek wzoru na kąt trójkąta

Wzór na znalezienie środka kąta trójkąta jest następujący:

rj12 kontra rj11

Niech w trójkącie D, F i G są punktami, w których dwusieczne kątów odpowiednio A, B i C przecinają się z bokami BC, AC i AB.

Kąt ∠AIB (gdzie I jest środkiem trójkąta) można obliczyć ze wzoru:

∠AIB = 180° – (połowa sumy kątów A i B)

LUB

∠AIB = 180° – (∠A + ∠B)/2

Jak znaleźć środek trójkąta

Istnieją dwie metody znajdowania środka trójkąta. W budownictwie punkt środkowy wyznaczamy rysując dwusieczne kątów trójkąta. W geometrii współrzędnych stosujemy wzór na określenie środka.

Korzystanie z geometrii współrzędnych : Znajdź środek trójkąta o współrzędnych podanych jako: A(2, 2), B(6, 2) i C(4, 5)

Według podanych informacji

• (X₁, I₁) = (2, 2)
• (X₂, I₂) = (6, 2)
• (X₃, I₃) = (4, 5)

Wiemy, że środek trójkąta to:

Ja(x, y) = {(topór ₁ + bx ₂ + cx ₃ )/(a + b + c), (jest ₁ + przez ₂ + c ₃ )/(a + b + c)}

Dla strony a: Odległość pomiędzy punktami B i C = √((6 – 4)²+ (2 – 5)²) = √8

Dla strony b: Odległość pomiędzy punktami A i C = √((2 – 4)²+ (2 – 5)²) = √13

Dla strony c: Odległość pomiędzy punktami A i B = √((6 – 2)²+ (2 – 2)²) = 4

Wstawiając wartości a, b, c do wzoru na środek, otrzymujemy:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4 )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Środek trójkąta ABC o współrzędnych wynosi (22/5,62/25)

Jak skonstruować środek trójkąta?

Aby skonstruować środek trójkąta, konieczne będzie użycie kompasu. Korzystając z kompasu, wykonaj poniższe kroki:

Krok 1: Połóż jeden koniec kompasu na wierzchołku trójkąta, a drugi koniec dotyka jednej strony.

Krok 2: Użyj kompasu, aby narysować dwa łuki po dwóch bokach trójkąta.

Krok 3: Mając tę ​​samą odległość na kompasie, utwórz dwa łuki wewnątrz trójkąta. Łuki te powinny przecinać się od miejsca, w którym stykają się z bokami.

Krok 4: Narysuj linię od wierzchołka trójkąta do miejsca, w którym przecinają się dwa wewnętrzne łuki.

Krok 5: Powtórz te same kroki z drugiego wierzchołka trójkąta.

Krok 6: Miejsce, w którym obie linie spotykają się lub przecinają, jest środkiem trójkąta.

Środek trójkąta prostokątnego

Centrum, jeśli a Kąt prosty trójkąt to punkt, w którym przecinają się wszystkie dwusieczne kątów trójkąta prostokątnego. Jeśli boki trójkąta prostokątnego mają wymiary a, b i c, wówczas promień okręgu „r” jest podawany jako r = (ab)/(a + b + c). Środek prawego trójkąta pokazano poniżej:

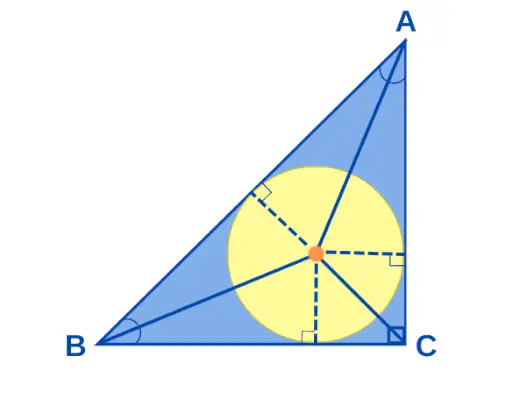
Środek trójkąta prostokątnego

Środek ciężkości, środek okręgu, środek wtrącony, ortocentrum

Środek ciężkości, środek okręgu, środek i ortocentrum to cztery ważne punkty związane z pociągiem. Porównanie środka ciężkości, środka okręgu, środka i ortocentrum przedstawiono w poniższej tabeli:

Sprawdź także

• Pole Trójkąta
• Obwód trójkąta
• Właściwość sumy kątów trójkąta

Przykłady środka trójkąta

Przykład 1: Oblicz środek trójkąta ABC. AB= 8cm, BC= 15 cm, CA= 17 cm.

Rozwiązanie:

Korzystając ze wzoru na środek trójkąta = (aA + bB + cC)/(a + b + c)

Gdzie,

• a = 8
• b = 15
• c = 17

A kąty są,

• A = 30°
• B = 60°
• C = 90°

Umieszczając te wartości we wzorze na otrzymanie,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Przykład 2: Jane obliczyła pole trójkątnego pola na 120 metrów kwadratowych. Obwód pola wynosi 36 metrów. Jeśli wewnątrz trójkąta narysowano okrąg w taki sposób, aby dotykał wszystkich boków trójkąta, pomóż Jane obliczyć promień trójkąta.

Rozwiązanie:

Według podanych informacji,

Pole trójkąta = 120 metrów kwadratowych

Obwód trójkąta = 36 metrów

Wiemy, że pole trójkąta = r × s

s = półobwód

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metra

Ćwicz problemy dotyczące środka trójkąta

Zadanie 1: Mając dany trójkąt PQR o wierzchołkach P(1, 2), Q(4, 6) i R(7, 2), znajdź współrzędne środka.

Zadanie 2: Skonstruuj trójkąt ABC o ∠A = 45°, ∠B = 60° i ∠C = 75°. Użyj metody konstrukcyjnej, aby znaleźć środek.

Zadanie 3: W trójkącie LMN, jeśli ∠L = 75°, ∠M = 60° i ∠N = 45°, znajdź współrzędne środka.

Zadanie 4: Skonstruuj trójkąt XYZ o ∠X = 80°, ∠Y = 50° i ∠Z = 50°. Użyj metody konstrukcyjnej, aby znaleźć środek.

Środek trójkąta: często zadawane pytania

Co to jest środek trójkąta?

Środek trójkąta to punkt, w którym przecinają się dwusieczne kątów wewnętrznych. Jest w równej odległości od wszystkich trzech boków trójkąta.

Jakie jest znaczenie środka w trójkącie?

Środek jest znaczący, ponieważ jest środkiem okręgu wpisanego w trójkąt, największego okręgu mieszczącego się wewnątrz trójkąta. Ma tę właściwość, że jest w równej odległości ze wszystkich stron.

Czy Centrum może znajdować się poza Trójkątem?

Nie, środek zawsze znajduje się wewnątrz trójkąta. Jest to punkt zbieżności dwusiecznych kątów i z definicji musi znajdować się w granicach trójkąta.

Jak zbudowane jest centrum za pomocą kompasu i prostej krawędzi?

Aby skonstruować środek, użyj kompasu i narysuj dwusieczne kąta z każdego wierzchołka na przeciwną stronę. Środek to punkt, w którym te dwusieczne się przecinają.

Co to jest formuła Incenter?

Wzór na środek trójkąta można zapisać jako:

frac{(aA+bB+cC)}{a+b+c}

Jakie są właściwości środka trójkąta?

Centrum ma kilka kluczowych właściwości. Jest w równej odległości od boków trójkąta, co oznacza, że ​​odległości do boków są równe. Jest to także punkt przecięcia dwusiecznych kątów, dzielący kąty na dwie równe części.

Jak określa się centrum?

Aby wyznaczyć środek, musisz znaleźć miejsce przecięcia dwusiecznych kątów. Można to zrobić za pomocą wzoru na środek lub rysując dwusieczne kąta i znajdując ich punkt przecięcia.

Jaka jest różnica między Incentre i Circumcentre?

Główną różnicą między centrum środkowym a środkiem otaczającym jest ich skupienie. Środek incenter dotyczy dwusiecznych kątów i jest środkiem okręgu wpisanego, natomiast środek okręgu opisanego zajmuje się dwusiecznymi prostopadłymi i jest środkiem okręgu opisanego.

Czy Incentre i Centroid są takie same?

Nie, środek i środek ciężkości są różne. Środek znajduje się w miejscu, w którym spotykają się dwusieczne kąta, podczas gdy środek ciężkości znajduje się w miejscu przecięcia środkowych. Mediany łączą wierzchołki ze środkiem przeciwnej strony.

Czy Incentre i Orthocentre to to samo?

Nie, środek i ortocentrum nie są takie same. Środek to punkt, w którym kąt przecina się na pół, podczas gdy ortocentrum obejmuje wysokości – linie wychodzące z każdego wierzchołka prostopadle do przeciwnej strony. Są to różne punkty w trójkącie.