Automat Skończony (FA) to najprostsza maszyna do rozpoznawania wzorców. Służy do charakteryzowania języka regularnego, na przykład: /baa+!/.
Służy także do analizowania i rozpoznawania wyrażeń w języku naturalnym. Automat skończony lub maszyna o skończonych stanach to maszyna abstrakcyjna, która ma pięć elementów lub krotek. Posiada zestaw stanów i zasad przechodzenia z jednego stanu do drugiego, ale zależy to od zastosowanego symbolu wejściowego. W oparciu o stany i zestaw reguł ciąg wejściowy może zostać zaakceptowany lub odrzucony. Zasadniczo jest to abstrakcyjny model komputera cyfrowego, który odczytuje ciąg wejściowy i zmienia swój stan wewnętrzny w zależności od aktualnego symbolu wejściowego. Każdy automat definiuje język, czyli zbiór ciągów, które akceptuje. Poniższy rysunek przedstawia niektóre istotne cechy ogólnej automatyzacji.
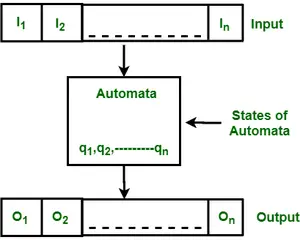
Postać: Cechy automatów skończonych
Powyższy rysunek przedstawia następujące cechy automatów:
- Wejście
- Wyjście
- Stany automatów
- Relacja państwowa
- Relacja wyjściowa
Automat skończony składa się z następujących elementów:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formalna specyfikacja maszyny to
podwójne w Javie
{ Q, ?, q, F, ? }> FA dzieli się na dwa typy:
1) Deterministyczne automaty skończone (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->P.> W DFA dla określonego znaku wejściowego maszyna przechodzi tylko do jednego stanu. Funkcja przejścia jest zdefiniowana dla każdego stanu dla każdego symbolu wejściowego. Również w DFA ruch zerowy (lub?) nie jest dozwolony, tj. DFA nie może zmienić stanu bez żadnego znaku wejściowego.
Na przykład skonstruuj DFA, który akceptuje język wszystkich ciągów kończących się na „a”.
Dany: ? = {a, b}, q = {q0}, F={q1}, Q = {q0, Q1}
Najpierw rozważ zestaw językowy wszystkich możliwych akceptowalnych ciągów znaków, aby skonstruować dokładny diagram przejść stanów.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, ojciec, ojciec, ojciec, ojciec}
Powyżej znajduje się prosty podzbiór możliwych akceptowalnych ciągów znaków, może być wiele innych ciągów kończących się na „a” i zawierających symbole {a, b}.
123 film
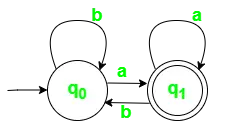
Ryc. 1. Diagram przejść stanu dla DFA z ? = {a, b}
Ciągi nieakceptowane to:
ab, bb, aab, abbb itd.
Tablica przejść stanów dla powyższego automatu,
| ?PaństwoSymbol? | A | B |
|---|---|---|
| Q0 | Q1 | Q0 |
| Q1 | Q1 | Q0 |
Należy zwrócić uwagę na jedną ważną rzecz: dla wzorca może istnieć wiele możliwych DFA . Generalnie preferowany jest DFA z minimalną liczbą stanów.
2) Niedeterministyczne automaty skończone (NFA): NFA jest podobny do DFA, z wyjątkiem następujących dodatkowych funkcji:
- Ruch zerowy (lub?) jest dozwolony, tj. może poruszać się do przodu bez czytania symboli.
- Możliwość transmisji do dowolnej liczby stanów dla danego wejścia.
Jednak powyższe funkcje nie dodają żadnej mocy NFA. Jeśli porównamy oba pod względem mocy, oba są równoważne.
Ze względu na powyższe dodatkowe funkcje, NFA ma inną funkcję przejścia, reszta jest taka sama jak DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Pytanie>
Jak widać, funkcja przejścia dotyczy dowolnego wejścia, włączając null (lub?), NFA może przejść do dowolnej liczby stanów. Na przykład poniżej znajduje się NFA dotyczące powyższego problemu.
co robi Ravel w Pythonie
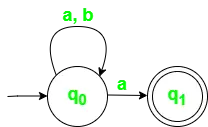
Ryc. 2. Diagram przejść stanu dla NFA z ? = {a, b}
Tabela przejść stanów dla powyższego automatu,
| ?PaństwoSymbol? | A | B |
|---|---|---|
| Q0 | {Q0,Q1} | Q0 |
| Q1 | ? | ? |
Należy zwrócić uwagę na jedną ważną rzecz: w NFA, jeśli jakakolwiek ścieżka ciągu wejściowego prowadzi do stanu końcowego, to ciąg wejściowy Jest przyjęty . Na przykład w powyższym NFA istnieje wiele ścieżek dla ciągu wejściowego 00. Ponieważ jedna ze ścieżek prowadzi do stanu końcowego, 00 jest akceptowane przez powyższy NFA.
Kilka ważnych punktów:
- Uzasadnienie:
In case of DFA ? : Q X ? -->Pyt. W przypadku NFA? : P X? --> 2Q>
Teraz, jeśli zaobserwujesz, dowiesz się Q X ? –> Q jest częścią Q X? –> 2Q.
Po stronie RHS Q jest podzbiorem 2Qco wskazuje, że Q jest zawarte w 2Qlub Q jest częścią 2Qjednak sytuacja odwrotna nie jest prawdą. Zatem matematycznie możemy to stwierdzić każde DFA to NFA, ale nie odwrotnie . Istnieje jednak sposób na konwersję NFA na DFA, tzw istnieje równoważny DFA dla każdego NFA .
- Zarówno NFA, jak i DFA mają tę samą moc, a każdy NFA można przełożyć na DFA.
- Może istnieć wiele stanów końcowych zarówno w DFA, jak i NFA.
- NFA to bardziej koncepcja teoretyczna.
- DFA jest używany w analizie leksykalnej w kompilatorze.
- Jeśli liczba stanów w NFA wynosi N, wówczas jego DFA może mieć maksymalnie 2Nliczba stanów.
Zobacz Quiz na temat wyrażeń regularnych i automatów skończonych.
