Biorąc pod uwagę dwa ciągi, S1 I S2 , zadaniem jest znalezienie długości najdłuższego podciągu wspólnego, czyli najdłuższego podciągu występującego w obu ciągach.
A najdłuższy wspólny podciąg (LCS) definiuje się jako najdłuższy podciąg, który jest wspólny dla wszystkich podanych ciągów wejściowych.
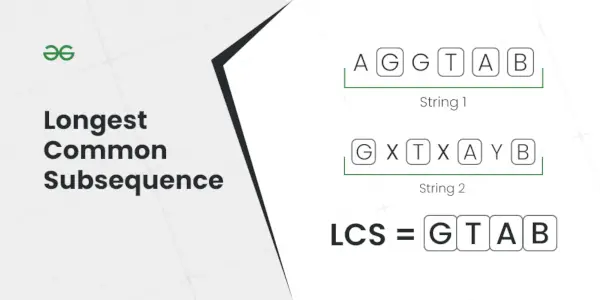
Najdłuższy wspólny podciąg
Przykłady:
Zalecana praktyka Najdłuższy wspólny podciąg Spróbuj!Wejście: S1 = ABC, S2 = ACD
Wyjście: 2
Wyjaśnienie: Najdłuższym podciągiem występującym w obu łańcuchach jest AC.Wejście: S1 = AGGTAB, S2 = GXTXAYB
Wyjście: 4
Wyjaśnienie: Najdłuższym wspólnym podciągiem jest GTAB.Wejście: S1 = ABC, S2 = CBA
Wyjście: 1
Wyjaśnienie: Istnieją trzy wspólne podciągi o długości 1, A, B i C i nie ma wspólnego podciągu o długości większej niż 1.Wejście: S1 = XYZW, S2 = XYWZ
Wyjście: 3
Wyjaśnienie: Istnieją dwa wspólne podciągi o długości 3 XYZ i XYW i nie ma wspólnego podciągu. o długości większej niż 3.sąsiednie kąty
Najdłuższy wspólny podciąg (LCS) przy użyciu rekurencji:
Wygeneruj wszystkie możliwe podciągi i znajdź najdłuższy z nich, który występuje w obu ciągach, używając Aby wdrożyć pomysł, wykonaj poniższe kroki:
- Utwórz funkcję rekurencyjną [powiedzmy lcs() ]
- Sprawdź relację pomiędzy pierwszymi znakami ciągów, które nie zostały jeszcze przetworzone.
- W zależności od relacji wywołaj następną funkcję rekurencyjną, jak wspomniano powyżej.
- Zwróć długość LCS otrzymaną jako odpowiedź.
Poniżej znajduje się implementacja podejścia rekurencyjnego:
C++C// A Naive recursive implementation of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n) // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; } // This code is contributed by rathbhupendra>Jawa// A Naive recursive implementation // of LCS problem #include int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j) // Utility function to get max of // 2 integers int max(int a, int b) { return (a>B) ? za: b; } // Kod sterownika int main() { char S1[] = 'BD'; znak S2[] = 'ABCD'; int m = strlen(S1); int n = strlen(S2); int i = 0, j = 0; // Wywołanie funkcji printf('Długość LCS wynosi %d', lcs(S1, S2, i, j)); zwróć 0; }>Pyton// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) n == 0) return 0; if (X.charAt(m - 1) == Y.charAt(n - 1)) return 1 + lcs(X, Y, m - 1, n - 1); else return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n)); // Utility function to get max of 2 integers int max(int a, int b) { return (a>B) ? za: b; } // Kod sterownika public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Łańcuch S1 = 'AGGTAB'; Ciąg S2 = 'GXTXAYB'; int m = S1.długość(); int n = S2.długość(); System.out.println('Długość LCS wynosi' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Autorem tego kodu jest Saket Kumar>C## A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>JavaScript// C# Naive recursive implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) if (m == 0 // Utility function to get max of 2 integers static int max(int a, int b) { return (a>B) ? za: b; } // Kod sterownika public static void Main() { String S1 = 'AGGTAB'; Ciąg S2 = 'GXTXAYB'; int m = S1.Długość; int n = S2.Długość; Console.Write('Długość LCS wynosi' + ' ' + lcs(S1, S2, m, n)); } } // Ten kod został napisany przez Sam007>PHP>
WyjścieLength of LCS is 4>Złożoność czasowa: O(2m+n)
Przestrzeń pomocnicza: O(1)Najdłuższy wspólny podciąg (LCS) przy użyciu Zapamiętywanie :
1. Optymalna podbudowa:
Zobacz rozwiązanie struktury L(X[0, 1, . . ., m-1], Y[0, 1, . . . n-1]) korzystamy z pomocy podstruktur X[0 , 1, …, m-2], Y[0, 1,…, n-2], w zależności od sytuacji (czyli optymalnego ich wykorzystania) w celu znalezienia rozwiązania całości.
aktorka Zeenat Aman2. Nakładające się podproblemy:
Jeśli zastosujemy powyższe podejście rekurencyjne dla ciągów BD I ABCD , otrzymamy częściowe drzewo rekurencji, jak pokazano poniżej. Widzimy tutaj, że podproblem L(BD, ABCD) jest obliczany więcej niż raz. Jeśli weźmie się pod uwagę całe drzewo, będzie kilka takich nakładających się podproblemów.
L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)Zbliżać się: Ze względu na obecność tych dwóch właściwości możemy rozwiązać problem za pomocą programowania dynamicznego lub zapamiętywania. Poniżej znajduje się podejście do rozwiązania wykorzystujące rekurencję.
- Utwórz funkcję rekurencyjną. Utwórz także tablicę 2D do przechowywania wyniku unikalnego stanu.
- Jeśli podczas wywołania rekursyjnego ten sam stan zostanie wywołany więcej niż raz, możemy bezpośrednio zwrócić odpowiedź zapisaną dla tego stanu, zamiast ponownie obliczać.
Poniżej implementacja powyższego podejścia:
C++Jawa// A Top-Down DP implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n, vector>& dp) { if (m == 0 || n == 0) return 0; if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); if (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Kod sterownika int main() { char X[] = 'AGGTAB'; znak Y[] = 'GXTXAYB'; int m = strlen(X); int n = strlen(Y); wektor > dp(m + 1, wektor (n + 1, -1)); cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp); return 0; }> Pyton/*package whatever //do not write package name here */ import java.io.*; class GFG { // A Top-Down DP implementation of LCS problem // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n, int[][] dp) { if (m == 0 || n == 0) return 0; if (dp[m][n] != -1) return dp[m][n]; if (X.charAt(m - 1) == Y.charAt(n - 1)) { dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); return dp[m][n]; } dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); return dp[m][n]; } // Drivers code public static void main(String args[]) { String X = 'AGGTAB'; String Y = 'GXTXAYB'; int m = X.length(); int n = Y.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 0; i < m + 1; i++) { for (int j = 0; j < n + 1; j++) { dp[i][j] = -1; } } System.out.println('Length of LCS is ' + lcs(X, Y, m, n, dp)); } } // This code is contributed by shinjanpatra>C## A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>JavaScript/* C# Naive recursive implementation of LCS problem */ using System; class GFG { /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ static int lcs(char[] X, char[] Y, int m, int n, int[, ] L) { if (m == 0 || n == 0) return 0; if (L[m, n] != -1) return L[m, n]; if (X[m - 1] == Y[n - 1]) { L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L); return L[m, n]; } L[m, n] = max(lcs(X, Y, m, n - 1, L), lcs(X, Y, m - 1, n, L)); return L[m, n]; } /* Utility function to get max of 2 integers */ static int max(int a, int b) { return (a>B) ? za: b; } public static void Main() { String s1 = 'AGGTAB'; Ciąg s2 = 'GXTXAYB'; char[] X = s1.ToCharArray(); char[] Y = s2.ToCharArray(); int m = X.Długość; int n = Y.Długość; int[, ] L = nowy int[m + 1, n + 1]; for (int i = 0; tj<= m; i++) { for (int j = 0; j <= n; j++) { L[i, j] = -1; } } Console.Write('Length of LCS is' + ' ' + lcs(X, Y, m, n, L)); } } // This code is contributed by akshitsaxenaa09>/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) { if (m == 0 || n == 0) return 0; if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp); if (dp[m][n] != -1) { return dp[m][n]; } return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) { dp[i] = new Array(n + 1).fill(-1); } console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
WyjścieLength of LCS is 4>Złożoność czasowa: O(m * n) gdzie m i n to długości strun.
Przestrzeń pomocnicza: O(m * n) Tutaj rekursywna przestrzeń stosu jest ignorowana.Najdłuższy wspólny podciąg (LCS) przy użyciu metody od dołu do góry (tabulacja):
Możemy wykonać następujące kroki, aby wdrożyć podejście programowania dynamicznego dla LCS.
- Utwórz tablicę 2D dp[][] z wierszami i kolumnami równymi długości każdego ciągu wejściowego plus 1 [liczba wierszy wskazuje indeksy S1 a kolumny wskazują indeksy S2 ]
- Zainicjuj pierwszy wiersz i kolumnę tablicy dp na 0.
- Iteruj po wierszach tablicy dp, zaczynając od 1 (powiedzmy, używając iterator I ).
- Dla każdego I , iteruj wszystkie kolumny z j = 1 do n :
- Jeśli S1[i-1] jest równe S2[j-1] , ustaw bieżący element tablicy dp na wartość elementu na ( dp[i-1][j-1] + 1 ).
- W przeciwnym razie ustaw bieżący element tablicy dp na maksymalną wartość dp[i-1] [j] I dp[i] [j-1] .
- Po zagnieżdżonych pętlach ostatni element tablicy dp będzie zawierał długość LCS.
Aby lepiej zrozumieć, zobacz poniższą ilustrację:
Ilustracja:
Powiedz, że sznurki są S1 = AGGTAB I S2 = GXTXAYB .
Pierwszy krok: Początkowo utwórz macierz 2D (powiedzmy dp[][]) o rozmiarze 8 x 7, której pierwszy wiersz i pierwsza kolumna są wypełnione wartością 0.
Tworzenie tabeli dp
Drugi krok: Trawers dla i = 1. Kiedy j staje się 5, S1[0] i S2[4] są równe. Zatem dp[][] jest aktualizowany. Dla pozostałych elementów przyjmujemy maksimum dp[i-1][j] i dp[i][j-1]. (W tym przypadku, jeśli obie wartości są równe, użyliśmy strzałek do poprzednich wierszy).
Wypełnianie wiersza nr 1
Trzeci krok: Podczas przejścia dla i = 2, S1[1] i S2[0] są takie same (oba są „G”). Zatem wartość dp w tej komórce jest aktualizowana. Pozostałe elementy są aktualizowane zgodnie z warunkami.
numpy linspaceWypełnienie wiersza nr. 2
Czwarty krok: Dla i = 3, S1[2] i S2[0] znów są takie same. Aktualizacje są następujące.
Wypełnianie wiersza nr. 3
Piąty krok: Dla i = 4 widzimy, że S1[3] i S2[2] są takie same. Zatem dp[4] [3] zaktualizowano jako dp[3] [2] + 1 = 2.
Wypełnianie rzędu 4
Szósty krok: Tutaj widzimy, że dla i = 5 i j = 5 wartości S1[4] i S2[4] są takie same (tj. oba są „A”). Zatem dp[5] [5] zostanie odpowiednio zaktualizowane i zmieni się na 3.
Wypełnianie rzędu 5
Ostatni krok: Dla i = 6 zobacz, że ostatnie znaki obu ciągów są takie same (są „B”). Dlatego wartość dp[6] [7] wynosi 4.
Wypełnianie ostatniego rzędu
piekło wywołania zwrotnego w javascriptOtrzymujemy więc maksymalną długość wspólnego podciągu jako 4 .
Poniżej znajduje się tabelaryczna implementacja problemu LCS.
C++Jawa// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) { // Initializing a matrix of size // (m+1)*(n+1) int L[m + 1][n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. Note that // L[i][j] contains length of LCS of // X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) if (i == 0 } // L[m][n] contains length of LCS // for X[0..n-1] and Y[0..m-1] return L[m][n]; } // Driver code int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; int m = S1.size(); int n = S2.size(); // Function call cout << 'Length of LCS is ' << lcs(S1, S2, m, n); return 0; }>Pyton// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence { // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(String X, String Y, int m, int n) { int L[][] = new int[m + 1][n + 1]; // Following steps build L[m+1][n+1] in bottom up // fashion. Note that L[i][j] contains length of LCS // of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X.charAt(i - 1) == Y.charAt(j - 1)) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } return L[m][n]; } // Utility function to get max of 2 integers int max(int a, int b) { return (a>B) ? za: b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence(); Łańcuch S1 = 'AGGTAB'; Ciąg S2 = 'GXTXAYB'; int m = S1.długość(); int n = S2.długość(); System.out.println('Długość LCS wynosi' + ' ' + lcs.lcs(S1, S2, m, n)); } } // Autorem tego kodu jest Saket Kumar>C## Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>JavaScript// Dynamic Programming implementation of LCS problem using System; class GFG { // Returns length of LCS for X[0..m-1], Y[0..n-1] static int lcs(String X, String Y, int m, int n) { int[, ] L = new int[m + 1, n + 1]; // Following steps build L[m+1][n+1] // in bottom up fashion. // Note that L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) j == 0) L[i, j] = 0; else if (X[i - 1] == Y[j - 1]) L[i, j] = L[i - 1, j - 1] + 1; else L[i, j] = max(L[i - 1, j], L[i, j - 1]); } return L[m, n]; } // Utility function to get max of 2 integers static int max(int a, int b) { return (a>B) ? za: b; } // Kod sterownika public static void Main() { String S1 = 'AGGTAB'; Ciąg S2 = 'GXTXAYB'; int m = S1.Długość; int n = S2.Długość; Console.Write('Długość LCS wynosi' + ' ' + lcs(S1, S2, m, n)); } } // Autorem tego kodu jest Sam007>PHP// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers function max(a, b) { if (a>b) zwrócić a; w przeciwnym razie zwróć b; } // Zwraca długość LCS dla X[0..m-1], Y[0..n-1] funkcja lcs(X, Y, m, n) { var L = new Array(m + 1); for(var i = 0; tj< L.length; i++) { L[i] = new Array(n + 1); } var i, j; /* Following steps build L[m+1][n+1] in bottom up fashion. Note that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */ for(i = 0; i <= m; i++) { for(j = 0; j <= n; j++) j == 0) L[i][j] = 0; else if (X[i - 1] == Y[j - 1]) L[i][j] = L[i - 1][j - 1] + 1; else L[i][j] = max(L[i - 1][j], L[i][j - 1]); } /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */ return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>// Dynamic Programming C# // implementation of LCS problem function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1] // in bottom up fashion . // Note: L[i][j] contains length of // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) if ($i == 0 } // L[m][n] contains the length of // LCS of X[0..n-1] & Y[0..m-1] return $L[$m][$n]; } // Driver Code $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed // by Shivi_Aggarwal ?>>
WyjścieLength of LCS is 4>Złożoność czasowa: O(m * n), co jest znacznie lepsze niż złożoność czasowa najgorszego przypadku implementacji naiwnej rekurencyjnej.
Przestrzeń pomocnicza: O(m * n), ponieważ algorytm używa tablicy o rozmiarze (m+1)*(n+1) do przechowywania długości wspólnych podciągów.Najdłuższy wspólny podciąg (LCS) przy użyciu metody od dołu do góry (optymalizacja przestrzeni):
- W powyższym podejściu tabelarycznym używamy L[i-1] [j] i L[i] [j] itd. Tutaj L[i-1] będzie odnosić się do poprzedniego wiersza macierzy L, a L[i] odnosi się do bieżący wiersz.
- Możemy przeprowadzić optymalizację przestrzeni, używając dwóch wektorów, jeden jest poprzedni, a drugi aktualny.
- Kiedy wewnętrzna pętla for kończy się, inicjujemy poprzednią równą bieżącej.
Poniżej implementacja:
C++Jawa// Dynamic Programming C++ implementation // of LCS problem #include using namespace std; int longestCommonSubsequence(string& text1, string& text2) { int n = text1.size(); int m = text2.size(); // initializing 2 vectors of size m vectorprev(m + 1, 0), cur(m + 1, 0); for (int idx2 = 0; idx2< m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } int main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call cout << 'Length of LCS is ' << longestCommonSubsequence(S1, S2); return 0; }> Pyton// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG { public static int longestCommonSubsequence(String text1, String text2) { int n = text1.length(); int m = text2.length(); // Initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // If matching if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1)) cur[idx2] = 1 + prev[idx2 - 1]; // Not matching else cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } prev = Arrays.copyOf(cur, m + 1); } return cur[m]; } public static void main(String[] args) { String S1 = 'AGGTAB'; String S2 = 'GXTXAYB'; // Function call System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } }>C#def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>JavaScriptusing System; class Program { static int LongestCommonSubsequence(string text1, string text2) { int n = text1.Length; int m = text2.Length; // initializing 2 arrays of size m int[] prev = new int[m + 1]; int[] cur = new int[m + 1]; for (int idx2 = 0; idx2 < m + 1; idx2++) cur[idx2] = 0; for (int idx1 = 1; idx1 < n + 1; idx1++) { for (int idx2 = 1; idx2 < m + 1; idx2++) { // if matching if (text1[idx1 - 1] == text2[idx2 - 1]) cur[idx2] = 1 + prev[idx2 - 1]; // not matching else cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]); } prev = cur; } return cur[m]; } static void Main() { string S1 = 'AGGTAB'; string S2 = 'GXTXAYB'; // Function call Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2)); } }>function longestCommonSubsequence(text1, text2) { const n = text1.length; const m = text2.length; // Initializing two arrays of size m let prev = new Array(m + 1).fill(0); let cur = new Array(m + 1).fill(0); for (let idx2 = 0; idx2 < m + 1; idx2++) { cur[idx2] = 0; } for (let idx1 = 1; idx1 < n + 1; idx1++) { for (let idx2 = 1; idx2 < m + 1; idx2++) { // If characters match if (text1[idx1 - 1] === text2[idx2 - 1]) { cur[idx2] = 1 + prev[idx2 - 1]; } // If characters don't match else { cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]); } } // Update the 'prev' array prev = [...cur]; } return cur[m]; } // Main function function main() { const S1 = 'AGGTAB'; const S2 = 'GXTXAYB'; // Function call console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
WyjścieLength of LCS is 4>Złożoność czasowa: O(m * n), która pozostaje taka sama.
Przestrzeń pomocnicza: O(m), ponieważ algorytm wykorzystuje dwie tablice o rozmiarze m.







