Termin Zapamiętywanie pochodzi od słowa łacińskiego memorandum ( zapamiętać ), co w amerykańskim angielskim jest powszechnie skracane do memo i oznacza przekształcenie wyników funkcji w coś do zapamiętania.
W informatyce zapamiętywanie służy do przyspieszania programów komputerowych poprzez eliminację powtarzalnego obliczania wyników i unikanie powtarzających się wywołań funkcji przetwarzających te same dane wejściowe.

Co to jest zapamiętywanie
Spis treści
- Co to jest zapamiętywanie?
- Dlaczego stosuje się zapamiętywanie>
- Gdzie stosować zapamiętywanie?
- Rodzaje zapamiętywania
- Jak technika zapamiętywania wykorzystywana w programowaniu dynamicznym?
- Czym różni się zapamiętywanie od tabulacji?
- Problemy z praktyką kodowania w zapamiętywaniu
- Często zadawane pytania
- 1) Czy zapamiętywanie jest lepsze niż DP?
- 2) Czy zapamiętywanie to to samo, co buforowanie?
- 3) Dlaczego zapamiętywanie odbywa się z góry na dół?
- 4) Czy zapamiętywanie wykorzystuje rekurencję?
- 5) Czy powinienem używać tabulacji czy zapamiętywania?
- 6) Gdzie stosuje się zapamiętywanie?
- 7) Dlaczego nazywa się to zapamiętywaniem?
- 8) W jaki sposób zapamiętywanie zmniejsza złożoność czasową?
- 9) Jaka jest różnica między zapamiętywaniem a buforowaniem?
- 10) Dlaczego tabulacja jest szybsza niż zapamiętywanie?
- Wniosek
Dlaczego stosuje się zapamiętywanie?
Zapamiętywanie jest specyficzną formą buforowanie w którym się używa Programowanie dynamiczne . Celem buforowania jest poprawa wydajności naszych programów i zapewnienie dostępności danych, które można później wykorzystać. Zasadniczo przechowuje obliczony wcześniej wynik podproblemu i wykorzystuje zapisany wynik dla tego samego podproblemu. Eliminuje to dodatkowy wysiłek związany z wielokrotnym obliczaniem tego samego problemu. Wiemy już, że jeśli ten sam problem pojawia się wielokrotnie, to ma on charakter rekurencyjny.
Gdzie stosować zapamiętywanie?
Możemy zastosować technikę zapamiętywania, gdzie wykorzystanie wcześniej obliczonych wyników pojawia się na zdjęciu. Tego rodzaju problem jest najczęściej używany w kontekście rekurencja , szczególnie w przypadku problemów, które się z tym wiążą nakładające się podproblemy .
Weźmy przykład, w którym ten sam podproblem powtarza się wielokrotnie.
Przykład pokazujący, gdzie używać zapamiętywania:
Let us try to find the factorial of a number .>
Poniżej znajduje się metoda rekurencyjna do znalezienia silni liczby:
int silnia(unsigned int n)
{
jeśli (n == 0)
zwróć 1;
zwróć n * silnia(n – 1);
}
Co się stanie, jeśli zastosujemy tę metodę rekurencyjną?
Jeśli napiszesz pełny kod dla powyższego fragmentu, zauważysz, że w kodzie będą 2 metody:
1. factorial(n) 2. main()>
Teraz, jeśli mamy wiele zapytań, aby znaleźć silnię, na przykład znalezienie silni 2, 3, 9 i 5, będziemy musieli wywołać metodę silni() 4 razy:
factorial(2) factorial(3) factorial(9) factorial(5)>
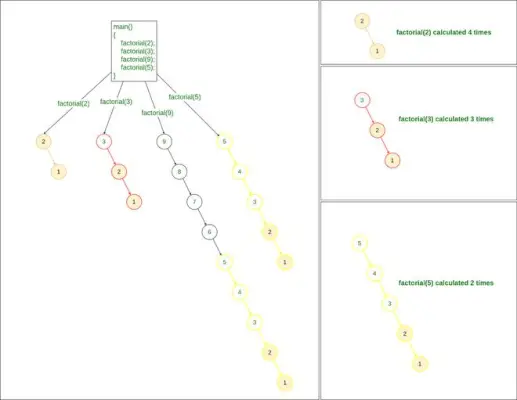
Rekurencyjna metoda znajdowania silni
Można więc śmiało powiedzieć, że do znalezienia silni liczb K potrzebna będzie złożoność czasowa O(N*K)
- NA) znaleźć silnię określonej liczby i
- STRZAŁKA) wywoływać metodę silni() K różne razy.
Jak zapamiętywanie może pomóc w rozwiązaniu takich problemów?
Jeżeli w powyższym zadaniu zauważymy, że przy obliczaniu silni 9:
drzewo binarne w Javie
- Obliczamy silnię liczby 2
- Obliczamy także silnię 3,
- i Obliczamy także silnię liczby 5
Dlatego też, jeśli zapiszemy wynik każdej indywidualnej silni przy pierwszym obliczeniu, możemy łatwo zwrócić silnię dowolnej wymaganej liczby w czasie O(1). Proces ten jest znany jako Zapamiętywanie .
Rozwiązanie wykorzystujące zapamiętywanie (Jak działa zapamiętywanie?):
Jeśli najpierw znajdziemy silnię liczby 9 i zapiszemy wyniki poszczególnych podproblemów, możemy łatwo wydrukować silnię każdego wejścia w O(1).
Dlatego znalezienie liczb silni za pomocą zapamiętywania będzie złożoność czasową NA)
- NA) aby znaleźć silnię największego wejścia
- O(1) aby wydrukować silnię każdego wejścia.
Rodzaje zapamiętywania
Wdrożenie zapamiętywania zależy od zmieniających się parametrów odpowiedzialnych za rozwiązanie problemu. W technice zapamiętywania stosuje się różne wymiary buforowania. Poniżej przedstawiono niektóre z nich:
- Zapamiętywanie 1D: Funkcja rekurencyjna posiadająca tylko jeden argument, którego wartość nie jest stała po każdym wywołaniu funkcji.
- Zapamiętywanie 2D: Funkcja rekurencyjna, która ma tylko dwa argumenty, a ich wartość nie jest stała po każdym wywołaniu funkcji.
- Zapamiętywanie 3D : Funkcja rekurencyjna, która ma tylko trzy argumenty, których wartości nie są stałe po każdym wywołaniu funkcji.
Jak technika zapamiętywania jest wykorzystywana w programowaniu dynamicznym?
Programowanie dynamiczne pomaga efektywnie rozwiązywać problemy, które mają nakładające się podproblemy i optymalne właściwości podstruktury. Ideą programowania dynamicznego jest podzielenie problemu na mniejsze podproblemy i zapisanie wyniku do wykorzystania w przyszłości, eliminując w ten sposób potrzebę wielokrotnego obliczania wyniku.
Istnieją dwa podejścia do formułowania rozwiązania w zakresie programowania dynamicznego:
- Podejście odgórne: Podejście to jest zgodne z zapamiętywanie technika . Składa się ona z rekurencja I buforowanie . W obliczeniach rekurencja reprezentuje proces wielokrotnego wywoływania funkcji, podczas gdy pamięć podręczna odnosi się do procesu przechowywania wyników pośrednich.
- Podejście oddolne: W tym podejściu wykorzystuje się tabulacja technika do wdrożenia rozwiązania programowania dynamicznego. Rozwiązuje te same problemy, co poprzednio, ale bez rekurencji. W tym podejściu iteracja zastępuje rekurencję. Dlatego nie występuje błąd przepełnienia stosu ani narzut procedur rekurencyjnych.
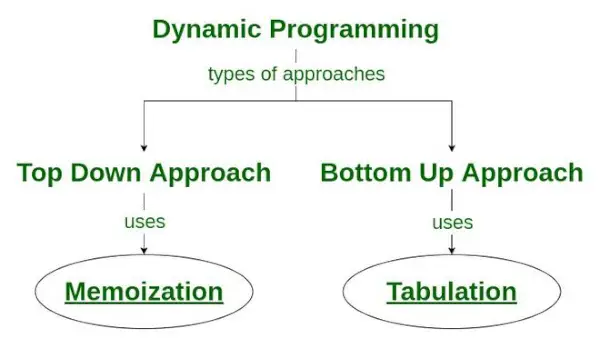
Jak technika zapamiętywania jest wykorzystywana w programowaniu dynamicznym
Czym różni się zapamiętywanie od tabulacji?

Tabulacja a zapamiętywanie
Więcej szczegółów znajdziesz na: Tabulacja a zapamiętywanie
Problemy z praktyką kodowania w zapamiętywaniu
| Pytanie | Artykuł | Ćwiczyć | Wideo |
|---|---|---|---|
| Policz sposoby dotarcia do n-tych schodów | Pogląd | Rozwiązywać | Oglądać |
| Problem z łamaniem wyrazów | DP-32 | Pogląd | Rozwiązywać | Oglądać |
| Program do liczb Fibonacciego | Pogląd | Rozwiązywać | Oglądać |
| n-ty numer kataloński | Pogląd | Rozwiązywać | Oglądać |
| Problem z kopalnią złota | Pogląd | Rozwiązywać | Oglądać |
| Problem z sumą podzbiorów | Pogląd | Rozwiązywać | Oglądać |
| Cięcie pręta | Pogląd | Rozwiązywać | Oglądać |
| Ścieżka kosztu minimalnego | Pogląd | Rozwiązywać | Oglądać |
| Minimalna liczba skoków do osiągnięcia końca | Pogląd | Rozwiązywać | Oglądać |
| Najdłuższy podciąg palindromowy | Zestaw 1 | Pogląd | Rozwiązywać | Oglądać |
| Najdłużej powtarzający się podciąg | Pogląd | Rozwiązywać | Oglądać |
| Policz sposoby dotarcia do n-tego stopnia, wykonując krok 1, 2 lub 3 | Pogląd | Rozwiązywać | Oglądać |
| Policz różne sposoby wyrażenia N jako sumy 1, 3 i 4 | Pogląd | Rozwiązywać | Oglądać |
| Policz liczbę sposobów pokonania dystansu | Pogląd | Rozwiązywać | Oglądać |
| Liczba tablic zawierających kolejny element o różnych wartościach | Pogląd | Rozwiązywać | Oglądać |
| Ciągła podtablica o największej sumie | Pogląd | Rozwiązywać | Oglądać |
| Ciągła podtablica o najmniejszej sumie | Pogląd | Rozwiązywać | Oglądać |
| Unikalne ścieżki w siatce z przeszkodami | Pogląd | Rozwiązywać | Oglądać |
| Różne sposoby sumowania n przy użyciu liczb większych lub równych m | Pogląd | Rozwiązywać | Oglądać |
Często zadawane pytania (FAQ) dotyczące zapamiętywania
1: Czy zapamiętywanie jest lepsze niż DP?
Zapamiętywanie to odgórne podejście do rozwiązywania problemu związanego z programowaniem dynamicznym. Nazywa się to zapamiętywaniem, ponieważ utworzymy notatkę dla wartości zwróconych w wyniku rozwiązania każdego problemu.
2: Czy zapamiętywanie to to samo, co buforowanie?
Zapamiętywanie jest właściwie specyficznym rodzajem buforowania. Termin buforowanie może ogólnie odnosić się do dowolnej techniki przechowywania (takiej jak buforowanie HTTP) do wykorzystania w przyszłości, ale zapamiętywanie odnosi się bardziej szczegółowo do funkcji buforowania, która zwraca wartość.
3: Dlaczego zapamiętywanie odbywa się odgórnie?
Podejście odgórne dzieli duży problem na wiele podproblemów. jeśli podproblem został już rozwiązany, użyj odpowiedzi ponownie. W przeciwnym razie rozwiąż podproblem i zapisz wynik w jakiejś pamięci.
4: Czy zapamiętywanie wykorzystuje rekurencję?
Zapamiętywanie opiera się na podejściu odgórnym do rozwiązania problemu. Składa się z rekurencji i buforowania. W obliczeniach rekurencja reprezentuje proces wielokrotnego wywoływania funkcji, podczas gdy pamięć podręczna odnosi się do procesu przechowywania wyników pośrednich.
5: Czy powinienem używać tabulacji czy zapamiętywania?
W przypadku problemów wymagających rozwiązania wszystkich podproblemów, tabulacja zwykle przewyższa zapamiętywanie o stały współczynnik. Dzieje się tak dlatego, że zestawienie nie powoduje narzutu rekurencji, co skraca czas rozwiązywania stosu wywołań rekurencji z pamięci stosu.
Ilekroć podproblem musi zostać rozwiązany, aby rozwiązać pierwotny problem, preferowane jest zapamiętywanie, ponieważ podproblem rozwiązuje się leniwie, tj. Wykonuje się tylko niezbędne obliczenia.
6: Gdzie stosuje się zapamiętywanie?
Zapamiętywanie to technika optymalizacji stosowana do przyspieszania programów komputerowych poprzez buforowanie wyników kosztownych wywołań funkcji i zwracanie ich w przypadku ponownego napotkania tych samych danych wejściowych.
7: Dlaczego nazywa się to zapamiętywaniem?
Termin zapamiętywanie pochodzi od łacińskiego słowa memorandum (pamiętać), które w amerykańskim angielskim jest powszechnie skracane do memo i które oznacza przekształcenie wyników funkcji w coś do zapamiętania.
8: W jaki sposób zapamiętywanie zmniejsza złożoność czasu?
Wielokrotne rozwiązywanie tego samego problemu wymaga czasu i zwiększa złożoność całego programu. Problem ten można rozwiązać, utrzymując pewną pamięć podręczną lub pamięć, w której będziemy przechowywać obliczony już wynik problemu dla określonych danych wejściowych. Jeśli więc nie chcemy przeliczać tego samego problemu, możemy po prostu skorzystać z wyniku zapisanego w pamięci i zmniejszyć złożoność czasową.
9: Jaka jest różnica między zapamiętywaniem a buforowaniem?
Zapamiętywanie to w rzeczywistości specyficzny rodzaj buforowania, który polega na buforowaniu wartości zwracanej przez funkcję na podstawie danych wejściowych. Buforowanie jest terminem bardziej ogólnym. Na przykład buforowanie HTTP jest buforowaniem, ale nie jest zapamiętywaniem.
10: Dlaczego tabulacja jest szybsza niż zapamiętywanie?
Tabulacja jest zwykle szybsza niż zapamiętywanie, ponieważ jest iteracyjna, a rozwiązywanie podproblemów nie wymaga narzutu związanego z wywołaniami rekurencyjnymi.
Zapamiętywanie to technika stosowana w informatyce w celu przyspieszenia wykonywania funkcji rekurencyjnych lub kosztownych obliczeniowo poprzez buforowanie wyników wywołań funkcji i zwracanie wyników z pamięci podręcznej, gdy ponownie wystąpią te same dane wejściowe.
Podstawową ideą zapamiętywania jest przechowywanie wyniku funkcji dla danego zestawu danych wejściowych i zwracanie wyniku z pamięci podręcznej, jeśli funkcja zostanie wywołana ponownie z tymi samymi danymi wejściowymi. Technika ta może zaoszczędzić czas obliczeń, zwłaszcza w przypadku funkcji, które są często wywoływane lub mają dużą złożoność czasową.
Oto przewodnik krok po kroku dotyczący wdrażania zapamiętywania:
Zidentyfikuj funkcję, którą chcesz zoptymalizować za pomocą zapamiętywania. Ta funkcja powinna wymagać powtarzalnych i kosztownych obliczeń dla tych samych danych wejściowych.
Utwórz obiekt słownika do przechowywania buforowanych wyników funkcji. Klucze słownika powinny być parametrami wejściowymi funkcji, a wartościami powinny być obliczone wyniki.
Na początku funkcji sprawdź, czy parametry wejściowe znajdują się już w słowniku pamięci podręcznej. Jeśli tak, zwróć wynik z pamięci podręcznej.
Jeśli parametrów wejściowych nie ma w słowniku pamięci podręcznej, oblicz wynik i zapisz go w słowniku pamięci podręcznej z parametrami wejściowymi jako kluczem.
Zwróć obliczony wynik.
Oto przykład kodu Pythona implementującego zapamiętywanie przy użyciu słownika:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
rozpakowywanie w Linuksie
>Wyjście
>
W powyższym kodzie definiujemy funkcję zwaną Fibonacci, która oblicza n-tą liczbę w ciągu Fibonacciego. Do przechowywania wyników wywołań funkcji używamy obiektu słownikowego zwanego pamięcią podręczną. Jeśli parametr wejściowy n jest już obecny w słowniku pamięci podręcznej, zwracamy wynik z pamięci podręcznej. W przeciwnym razie obliczamy wynik za pomocą rekurencyjnych wywołań funkcji Fibonacciego i przechowujemy go w słowniku pamięci podręcznej przed zwróceniem.
Zapamiętywanie można wykorzystać do optymalizacji wydajności wielu funkcji, które wymagają powtarzalnych i kosztownych obliczeń. Buforując wyniki wywołań funkcji, możemy uniknąć niepotrzebnych obliczeń i przyspieszyć wykonanie funkcji.
Wniosek
Zapamiętywanie to koncepcja programowania, którą można zastosować w dowolnym języku programowania. Jego absolutnym celem jest optymalizacja programu. Zwykle ten problem występuje, gdy programy wykonują ciężkie obliczenia. Ta technika buforuje wszystkie poprzednie obliczone wyniki, dzięki czemu nie trzeba ich ponownie obliczać dla tego samego problemu.
Powiązane artykuły:
- Zapamiętywanie przy użyciu dekoratorów w Pythonie
- Zapamiętywanie JavaScriptu
