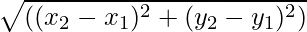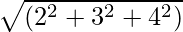logo

TechCodeview

Wielkość wektora

Wielkości wektorowe to wielkości, które mają zarówno kierunek, jak i wielkość. Wielkość wektora to długość wektora. Jest ona wyrażana przez wartość liczbową wektora i ponieważ reprezentuje długość wektora, jest więc zawsze dodatnia. Dla dowolnego wektora 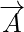overrightarrow{A}jego wielkość jest reprezentowana jako overrightarrow{A}.

Dowiedzmy się więcej o wielkości wektora, jego wzorze, przykładach i innych w tym artykule.



Spis treści

Jaka jest wielkość wektora?

Wielkość wektora definiuje się jako długość wektora. Ponieważ wielkość wektora oznacza długość wektora, jest on zawsze dodatni. Dla dowolnego wektora A jego wielkość jest reprezentowana jako |A|. Załóżmy, że wektor jest zdefiniowany jako xi + yj, a jego wielkość jest zdefiniowana jako pierwiastek kwadratowy z sumy kwadratów poszczególnych wyrazów. Wielkość wektora reprezentuje długość wektora, tj. wartość lub wpływ, jaki wektor ma.

Na przykład, jeśli na obiekt działa siła 5i N, to jej wielkość wynosi 5 N, co oznacza, że ​​siła przyłożonej siły wynosi 5 N, oraz I' w 5i oznacza, że ​​jest on stosowany w dodatnim kierunku x.



Wielkość wzoru wektorowego

Istnieją różne sposoby obliczania wielkości wektora. Na podstawie podanych danych użyj innego rodzaju wzoru, aby znaleźć wielkość wektora. Wielkość wektora A jest reprezentowana za pomocą operatora modułu, tj. |A|

Istnieją różne wzory używane do obliczania wielkości wektora. Poniższy obrazek przedstawia ważne wzory używane do wyznaczania wielkości wektora.

Wielkość wzoru wektorowego

Poniżej przedstawiono sposoby obliczania wielkości.



  • Jeżeli dany jest im wektor Ā = xi+ yĵ + zk̂, to wielkość wektora Ā można obliczyć korzystając z poniższego wzoru

Wielkość wektora Ā (|A|) = √(x 2 + i 2 +z 2 )

  • Jeśli wektor punktu początkowego to powiedz (x1, I1), a punkt końcowy wektora to powiedzmy (x2, I2) podaje się wówczas wielkość wektora overrightarrow{AB}jest dany przez,
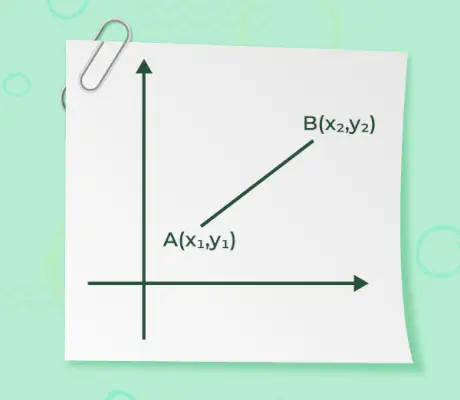
Wielkość wektora, jeśli podane są dwa punkty

Jeśli podany jest początek i koniec wektora, wielkość wektora to nic innego jak odległość między punktami. Wzór na znalezienie wielkości jest podany przez

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Jeśli którykolwiek z punktów początkowych lub końcowych wektora znajduje się w początku o(0, 0), a inny punkt jest A(x, y) jak pokazano na poniższym rysunku,
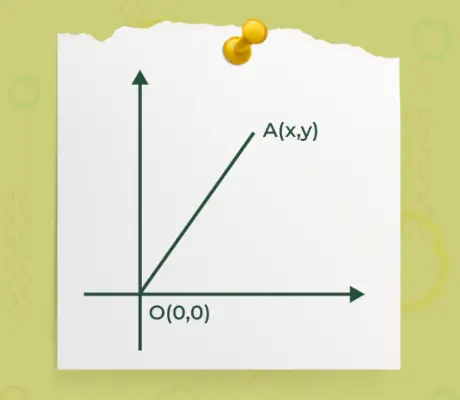
Wielkość wektora, jeśli podany jest jeden punkt i początek

Następnie podaje się wzór na znalezienie wielkości wektora, w którym jeden z końców wektora znajduje się w początku

|Ā| = √(x 2 +y 2 )

Kierunek wektora

Wielkości wektorowe to wielkości, które mają zarówno wielkość, jak i kierunek. Kierunek wielkości wektora oznacza, w którym kierunku stosowana jest wielkość wektora. Definiuje się go jako kąt, jaki wektor tworzy z linią poziomą lub osią x. Jest reprezentowany przez symbol A .

Poniższy obrazek przedstawia strzałkę używaną do wskazania kierunku wektora.

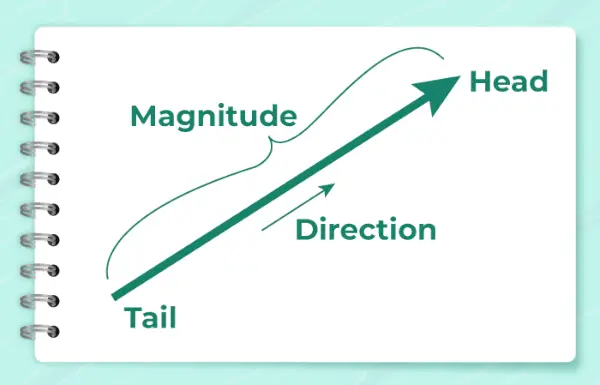
Kierunek wektora

Oblicza się go za pomocą wzoru,

α = opalenizna -1 (t/x)

wybierz sql z wielu tabel

Dla wektora wygenerowanego przez współrzędne (x1, I1) i (x2, I2) ich kierunek wyznacza wzór,

α = opalenizna -1 [(I 2 - I 1 )/(X 2 - X 1 )]

Jak znaleźć wielkość wektora?

Wielkość wektora oblicza się, stosując kroki omówione poniżej,

Krok 1: Zidentyfikuj składowe x, y i z wektora.

Krok 2 : Znajdź kwadraty wszystkich składników x, y i z.

Krok 3: Dodaj wszystkie kwadraty znalezione w kroku 2.

Krok 4: Znajdź pierwiastek kwadratowy z sumy otrzymanej w kroku 3.

Wartość uzyskana po kroku 4 jest wielkością danego wektora.

Przykład: Znajdź wielkość wektora A = 3i + 4j

Rozwiązanie:

Wielkość wektora A oblicza się, stosując kroki omówione powyżej.

jak zwrócić tablicę Java

Krok 1: Porównując A = 3i + 4j z xi + yj otrzymujemy x = 3 i y = 4

Krok 2: X2= 32= 9 i y2= 42= 16

Krok 3: X2+ i2= 9 + 16 = 25

Krok 4: √(25) = 5

Zatem wielkość wektora A = 3i + 4j wynosi 5 jednostek.

Wniosek

Podsumowując, wielkość wektora mówi nam, jak długi jest wektor. Koncepcja ta jest bardzo ważna w wielu dziedzinach, takich jak fizyka, inżynieria i informatyka, ponieważ pomaga mierzyć takie rzeczy, jak prędkość, siła i kierunek ruchu. Rozumiejąc wielkość wektora, możemy lepiej analizować i rozwiązywać problemy praktyczne, co czyni ją kluczową wiedzą dla każdego, kto pracuje z liczbami i pomiarami w rzeczywistych zastosowaniach.

Czytaj więcej,

Rozwiązane przykłady dotyczące wielkości wektora

Przykład 1: Znajdź wielkość wektora Ā = 2i + 3ĵ + 4k.

Rozwiązanie:

przejazd w przedsprzedaży

Dany,

Ā = 2i + 3ĵ + 4k

Wielkość |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Wielkość wektora 2i+3ĵ+4k Jest 5,38 jednostka

Przykład 2: Znajdź wielkość wektora Ā = 3i + 3ĵ – 6k

Rozwiązanie:

Dany

Ā = 3i + 3ĵ – 6k

Wielkość |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Wielkość wektora 3i+ 3ĵ – 6k Jest 7.35 jednostka.

Przykład 3: Znajdź wielkość wektora, jeśli punkt początkowy wektora to (3, 4), a punkt końcowy to (6, 2).

Rozwiązanie:

Dany,

(X1, I1) = (3, 4)
(X2, I2) = (6, 2)

przykład lambdy w Javie

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Zatem wielkość danego wektora wynosi 3.6 jednostka.

Przykład 4: Znajdź wielkość wektora, jeśli punkt początkowy wektora to (2, 1, 4), a punkt końcowy to (5, 2, 6).

Rozwiązanie:

Dany,

(X1, I1, z1) = (2, 1, 4)

(X2, I2, z2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Zatem wielkość danego wektora wynosi 3,74 jednostka.

Przykład 5: Jaka jest wielkość wektora rozpoczynającego się w punkcie początkowym i końcowym w (3, 4).

Rozwiązanie:

Dany,

Punktem początkowym wektora jest O(0, 0)

Punkt końcowy (x, y) = (3, 4)

Wielkość wektora (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Zatem wielkość danego wektora wynosi 5 jednostka.

Przykład 6: Znajdź wielkość wektora, którego jeden z punktów końcowych znajduje się w początku, a drugi w (1, 4, 3).

Rozwiązanie:

Dany,

Punkt końcowy wektora to O(0, 0)

Inny punkt (x, y, z) = (1, 4, 3)

Wielkość wektora (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Zatem wielkość danego wektora wynosi 5.09 jednostka.

jednostka arytmetyczno-logiczna

Często zadawane pytania dotyczące wielkości wektora

Jaka jest wielkość wzoru wektorowego?

Wielkość wektora jest wartością liczbową wektora i określa jego długość. Dla dowolnego wektora A jego wielkość jest reprezentowana jako |A|. Wielkość wektora oblicza się ze wzoru:

Dla dowolnego wektora A = xi + yj + zk jego wielkość jest określona wzorem

|A| = √(x 2 + i 2 + z 2 )

Dla dowolnego wektora, którego punkt początkowy i końcowy są odpowiednio (x1, I1) i (x2, I2) jego wielkość jest określona wzorem

|A| = √((x 2 - X 1 ) 2 + (i 2 - I 1 ) 2 )

Jak przedstawić wielkość wektora?

Wielkość wektora A jest reprezentowany przez symbol |A|.

Jak znaleźć wielkość wektora?

Do obliczenia wielkości wektora stosuje się różne wzory, niektóre z nich to:

  • |A| = √(x 2 + i 2 + z 2 ) gdy wektor ma postać A = xi + yj + zk
  • |A| = √((x) 2 + (i) 2 ) gdy wektor jest dany przez punkt A (x, y) i początek O(0, 0).
  • |A| = √((x 2 - X 1 ) 2 + (i 2 - I 1 ) 2 ) gdy wektor jest dany przez punkt A (x1, I2) i punkt B (x2, I2).

Znajdź wektor wielkości 5.

Istnieją różne wektory, które mogą mieć wielkość 5, czego przykładem jest wektor A przedstawiony jako:

A = 3i + 4j Lub A = 4i + 5j