Objętość kuli to ilość cieczy, jaką może pomieścić kula. Objętość kuli wyraża się jako 4/3πr³. Jest to przestrzeń zajmowana przez kulę w przestrzeni trójwymiarowej. Mierzy się go w jednostkach³tj. m³, cm³itp. Kula jest trójwymiarowym obiektem bryłowym o okrągłej formie w geometrii.

Objętość kuli to całkowita przestrzeń zajmowana przez powierzchnię kuli i jest proporcjonalna do sześcianu promienia kuli. W tym artykule dowiemy się szczegółowo o objętości kuli, wzorze objętości kuli, przykładach wzorów objętości kuli i innych szczegółach.

• Co to jest objętość kuli?
• Formuła objętości kuli
• Objętość stałej kuli
• Objętość pustej kuli
• Objętość wyprowadzenia wzoru na kulę
• Jak obliczyć objętość kuli?

Co to jest objętość kuli?

Objętość kuli to ilość miejsca, jaką w niej zajmuje. Kula jest trójwymiarowym, okrągłym, bryłowym kształtem, w którym wszystkie punkty na jej powierzchni są równomiernie oddalone od jej środka. Stała odległość to promień kuli, a stały punkt to środek kuli. Gdy okrąg się obróci, zauważymy zmianę formy. W wyniku obrotu dwuwymiarowego obiektu zwanego kołem uzyskuje się trójwymiarowy kształt kuli.

Ucz się więcej,

• Kula
• Powierzchnia kuli

Definicja objętości kuli

Objętość kuli to całkowita masa zawarta w powierzchni kuli. Jest to trójwymiarowa przestrzeń wewnątrz kuli. To zależy od promienia kuli. Dodany poniżej obrazek przedstawia kulę o promieniu r i jej objętość.

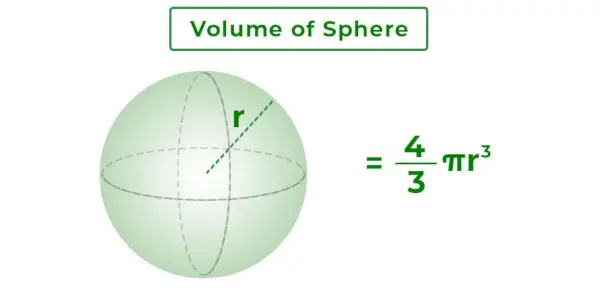
Formuła objętości kuli

Wzór na objętość kuli to wzór używany do obliczenia objętości kuli, gdy podany jest jej promień. Poniżej dodano objętość kuli na kulę o promieniu R,

Objętość kuli Wzór = 4/3πr ³

Gdzie,

• R jest promieniem kuli
• Liczba Pi jest stałą i jej wartość wynosi 22/7

Kulę ogólnie dzieli się na dwie, które są:

• Objętość stałej kuli
• Objętość pustej kuli

Poznajmy je szczegółowo.

Objętość stałej kuli

Kula pełna to kula całkowicie wypełniona aż do środka. tj. ma masę aż do rdzenia, a wzór na objętość, gdy jego promień wynosi r, wynosi:

Objętość stałej kuli (V) = (4/3)πr ³

Objętość pustej kuli

W przypadku pustej kuli jej przestrzeń wewnętrzna jest pusta i załóżmy, że jej promień zewnętrzny jest pusty R a jego promień wewnętrzny wynosi R, następnie oblicza się jego objętość ze wzoru,

Objętość pustej kuli = (4/3)π(R ³ - R ³ )

Objętość wyprowadzenia wzoru na kulę

Objętość kuli można wyznaczyć następującymi metodami:

• Korzystanie z integracji
• Korzystanie z zależności Archimedesa między cylindrem, stożkiem i kulą

Omówmy te metody szczegółowo w następujący sposób:

Objętość kuli przy użyciu całkowania

Stosując podejście całkujące, możemy po prostu obliczyć objętość kuli.

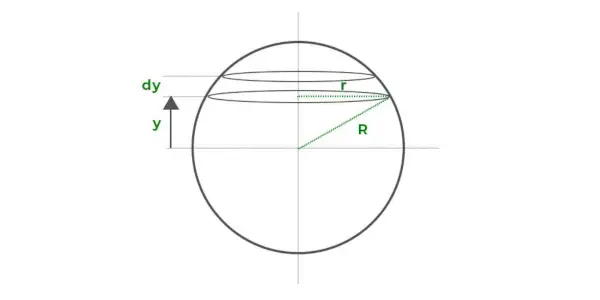
Załóżmy, że objętość kuli składa się z szeregu cienkich okrągłych krążków ułożonych jeden na drugim, jak pokazano na powyższym schemacie. Każdy cienki dysk ma promień r i grubość dy, która jest odległością y od osi x.

Niech objętość dysku będzie wynosić dV. Wartość dV jest podana przez,

dV = (πr²) Ty

Zatem dV = π (R²- I²) Ty

Całkowita objętość kuli będzie sumą objętości wszystkich tych małych krążków. Wymaganą wartość można uzyskać całkując wyrażenie z limitu -R do R.

Zatem objętość kuli staje się

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

W ten sposób wyprowadzamy wzór na objętość kuli.

Objętość kuli przy użyciu relacji Archimedesa

Jak już Archimedes udowodnił, jeśli stożek, kula i walec mają ten sam promień r i tę samą wysokość, to ich objętości są w stosunku 1:2:3.

Dlatego możemy powiedzieć:

Objętość cylindra = objętość stożka + objętość kuli

Zatem objętość kuli = objętość cylindra – objętość stożka

Jak wiemy, objętość cylindra = πr²h i objętość stożka = (1/3)πr²H

Podstawiając te wartości do równania otrzymujemy:

Objętość kuli = πr²h – (1/3)πr²h = (2/3)πr²H

Zakładamy, że wysokość walca jest równa średnicy kuli, która wynosi 2r. Zatem:

Objętość kuli wynosi (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Sprawdź także

• Wzór na objętość czapki sferycznej
• Formuła sektora sferycznego
• Formuła segmentu sferycznego

Jak obliczyć objętość kuli?

Objętość kuli to przestrzeń zajmowana przez kulę. Jego objętość można obliczyć ze wzoru V = 4/3πr ³ .

Aby obliczyć objętość kuli, należy wykonać następujące kroki:

Krok 1: Zaznacz wartość promienia kuli.

2 września: Znajdź sześcian promienia.

Krok 3: Pomnóż sześcian promienia przez (4/3)π

Krok 4: Dodaj (jednostkę)³do ostatecznej odpowiedzi.

Przykład obliczenia objętości kuli

Przykład: Znajdź objętość kuli o promieniu 7 cm.

Biorąc pod uwagę, r = 7 cm

V = (4/3)πr³

Objętość kuli, V = ((4/3) × π × 7³) cm³

Wysokość = 1436,8 cm³

Zatem objętość kuli wynosi 1436,8 cm³

Czytaj więcej

• Objętość stożka
• Objętość sześcianu
• Objętość cylindra

Objętość przykładów kuli

Przykład 1. Znajdź objętość kuli o promieniu 9 cm.

Rozwiązanie:

Mamy, r = 9

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (9) (9) (9)

⇒ Objętość kuli = (4) (3,14) (3) (9) (9)

⇒ Objętość kuli = 3052 cm³

Przykład 2. Znajdź objętość kuli o promieniu 12 cm.

Rozwiązanie:

Mamy, r = 12

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (12) (12) (12)

⇒ Objętość kuli = (4) (3,14) (4) (12) (12)

⇒ Objętość kuli = 7234,56 cm³

Przykład 3. Znajdź objętość kuli o promieniu 6 cm.

Rozwiązanie:

Mamy, r = 6

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (6) (6) (6)

⇒ Objętość kuli = (4) (3,14) (2) (6) (6)

⇒ Objętość kuli = 904,32 cm³

Przykład 4. Znajdź objętość kuli o promieniu 4 cm.

Rozwiązanie:

Mamy, r = 4

Objętość kuli = 4/3 πr3

⇒ Objętość kuli = (4/3) (3,14) (4) (4) (4)

⇒ Objętość kuli = (1,33) (3,14) (4) (4) (4)

⇒ Objętość kuli = 267,27 cm³

Przykład 5. Znajdź objętość kuli o średnicy 10 cm.

Rozwiązanie:

Mamy, 2r = 10

czytanie Java w CSV

⇒ r = 5

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (5) (5) (5)

⇒ Objętość kuli = (1,33) (3,14) (5) (5) (5)

⇒ Objętość kuli = 522,025 cm³

Przykład 6. Znajdź objętość kuli o średnicy 16 cm.

Rozwiązanie:

Mamy, 2r = 16

⇒ r = 8

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (8) (8) (8)

⇒ Objętość kuli = (1,33) (3,14) (8) (8) (8)

⇒ Objętość kuli = 2138,21 cm³

Przykład 7. Znajdź objętość kuli o średnicy 14 cm.

Rozwiązanie:

Mamy, 2r = 14

⇒ r = 7

Objętość kuli = 4/3 πr³

⇒ Objętość kuli = (4/3) (3,14) (7) (7) (7)

⇒ Objętość kuli = (1,33) (3,14) (7) (7) (7)

⇒ Objętość kuli = 1432,43 cm³

Tom pytań dotyczących praktyki sferycznej

Pytanie 1: Znajdź objętość kuli o średnicy 34 cm.

Pytanie 2: Znajdź objętość wydrążonej kuli, której promień wewnętrzny wynosi 4 cm, a promień zewnętrzny 8 cm.

Pytanie 3: Znajdź objętość kuli o promieniu 14 cm.

Pytanie 4: Jaka jest objętość kuli, której promień jest równy bokowi kwadratu o polu 144 m².

Tom Sfery-FAQ

Co to jest objętość kuli?

Objętość kuli to przestrzeń zajmowana przez powierzchnię kuli.

Jakie jest pole powierzchni wzoru na kulę?

Całkowita powierzchnia kuli o promieniu r wynosi, Powierzchnia = 4πr ²

Jaki jest wzór na objętość kuli?

Objętość kuli o promieniu r wynosi, Objętość = 4/3πr ³

Jak znaleźć objętość półkuli?

Objętość półkuli o promieniu r wynosi Objętość = 2/3πr ³

Jaki jest stosunek objętości kuli i półkuli?

Jeżeli kula i półkula mają ten sam promień, wówczas stosunek ich objętości wynosi:

W ₁ : W ₂ = (4/3πr ³ ) : (2/3πr ³ ) = 2 : 1

Jaka jest jednostka objętości kuli?

Objętość kuli mierzy się w m³, cm³, litry itp. M ³ jest standardową jednostką miary.

Jaka jest objętość kuli, gdy jej promień jest zmniejszony o połowę?

Objętość kuli = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Tom/8. Zatem objętość kuli wynosi jedną ósmą.