A Kopia binarna jest kompletne drzewo binarne który służy do wydajnego przechowywania danych, aby uzyskać element max lub min na podstawie jego struktury.
Sterta binarna to sterta minimalna lub sterta maksymalna. W minimalnej stercie binarnej klucz w katalogu głównym musi być minimalny spośród wszystkich kluczy znajdujących się w stercie binarnej. Ta sama właściwość musi być rekurencyjnie prawdziwa dla wszystkich węzłów w drzewie binarnym. Max Binary Heap jest podobny do MinHeap.
Przykłady Min Heap:
10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40
Jak reprezentowana jest sterta binarna?
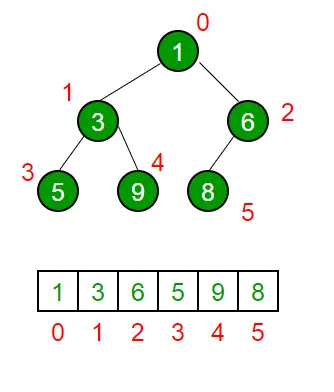
Kopia binarna to a Kompletne drzewo binarne . Kopiec binarny jest zwykle reprezentowany jako tablica.
- Element główny będzie znajdował się w Arr[0].
- Poniższa tabela przedstawia indeksy innych węzłów dla itwęzeł, tj. Arr[i]:
| Arr[(i-1)/2] | Zwraca węzeł nadrzędny |
| Arr[(2*i)+1] | Zwraca lewy węzeł podrzędny |
| Arr[(2*i)+2] | Zwraca prawy węzeł podrzędny |
Metodą przechodzenia w celu uzyskania reprezentacji tablicy jest Przechodzenie przez poziom zamówienia . Należy zapoznać się Reprezentacja tablicowa sterty binarnej dla szczegółów.
Operacje na stercie:
Poniżej znajduje się kilka standardowych operacji na stercie min:
- pobierzMin(): Zwraca element główny Min Heap. Czas Złożoność tej operacji wynosi O(1) . W przypadku maxheap byłoby to możliwe pobierzMax() .
- ekstraktMin() : Usuwa minimalny element z MinHeap. Złożoność czasowa tej operacji wynosi O(log N) ponieważ ta operacja musi zachować właściwość sterty (poprzez wywołanie zebrać() ) po usunięciu korzenia.
- zmniejszKlucz() : Zmniejsza wartość klucza. Złożoność czasowa tej operacji wynosi O(log N) . Jeśli zmniejszona wartość klucza węzła jest większa niż wartość klucza nadrzędnego węzła, nie musimy nic robić. W przeciwnym razie musimy przejść w górę, aby naprawić naruszoną właściwość sterty.
- wstawić() : Włożenie nowego klucza trwa O(log N) czas. Dodajemy nowy klucz na końcu drzewa. Jeśli nowy klucz jest większy niż jego rodzic, nie musimy nic robić. W przeciwnym razie musimy przejść w górę, aby naprawić naruszoną właściwość sterty.
- usuwać() : Usunięcie klucza również trwa O(log N) czas. Zamieniamy klucz do usunięcia na minimum nieskończone dzwoniąc zmniejszKlucz() . Po zmniejszeniuKey() wartość minus nieskończona musi osiągnąć pierwiastek, więc wywołujemy ekstraktMin() aby wyjąć klucz.
Poniżej znajduje się implementacja podstawowych operacji na stercie.
C++
// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>'
Overflow: Could not insertKey
'>;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest != i) { swap(&harr[i], &harr[smallest]); MinHeapify(smallest); } } // A utility function to swap two elements void swap(int *x, int *y) { int temp = *x; *x = *y; *y = temp; } // Driver program to test above functions int main() { MinHeap h(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); cout << h.extractMin() << ' '; cout << h.getMin() << ' '; h.decreaseKey(2, 1); cout << h.getMin(); return 0; }> |
>
>
to jest
Jawa
// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0> && heapArray[i] swap(heapArray, i, parent(i)); i = parent(i); } return true; } // Decreases value of given key to new_val. // It is assumed that new_val is smaller // than heapArray[key]. public void decreaseKey(int key, int new_val) { heapArray[key] = new_val; while (key != 0 && heapArray[key] swap(heapArray, key, parent(key)); key = parent(key); } } // Returns the minimum key (key at // root) from min heap public int getMin() { return heapArray[0]; } // Method to remove minimum element // (or root) from min heap public int extractMin() { if (current_heap_size <= 0) { return Integer.MAX_VALUE; } if (current_heap_size == 1) { current_heap_size--; return heapArray[0]; } // Store the minimum value, // and remove it from heap int root = heapArray[0]; heapArray[0] = heapArray[current_heap_size - 1]; current_heap_size--; MinHeapify(0); return root; } // This function deletes key at the // given index. It first reduced value // to minus infinite, then calls extractMin() public void deleteKey(int key) { decreaseKey(key, Integer.MIN_VALUE); extractMin(); } // A recursive method to heapify a subtree // with the root at given index // This method assumes that the subtrees // are already heapified private void MinHeapify(int key) { int l = left(key); int r = right(key); int smallest = key; if (l smallest = l; } if (r smallest = r; } if (smallest != key) { swap(heapArray, key, smallest); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } // Driver Code class MinHeapTest { public static void main(String[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); System.out.print(h.extractMin() + ' '); System.out.print(h.getMin() + ' '); h.decreaseKey(2, 1); System.out.print(h.getMin()); } } // This code is contributed by rishabmalhdijo> |
>
>
Pyton
# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
co to jest jajko wielkanocne na Androida
// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if> (l heapArray[l] { smallest = l; } if (r heapArray[r] { smallest = r; } if (smallest != key) { Swap(ref heapArray[key], ref heapArray[smallest]); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] { increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } static class MinHeapTest{ // Driver code public static void Main(string[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); Console.Write(h.extractMin() + ' '); Console.Write(h.getMin() + ' '); h.decreaseKey(2, 1); Console.Write(h.getMin()); } } // This code is contributed by // Dinesh Clinton Albert(dineshclinton)> |
>
>
JavaScript
// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && tablica[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]] this.MinHeapify(smallest); } } } let h = new MinHeap(); h.insert(3); h.insert(2); h.deleteKey(1); h.insert(15); h.insert(5); h.insert(4); h.insert(45); console.log(h.extractMin() + ' '); console.log(h.getMin() + ' '); h.decreaseKey(2, 1); console.log(h.extractMin());> |
nie jest równy mysql
>
>Wyjście
2 4 1>
Zastosowania stosów:
- Sortowanie sterty : Sortowanie sterty wykorzystuje stertę binarną do sortowania tablicy w czasie O(nLogn).
- Kolejka priorytetowa: Kolejki priorytetowe można skutecznie implementować przy użyciu sterty binarnej, ponieważ obsługuje ona operacje wstawiane(), usuwane() i ekstraktmax(), zmniejszaKey() w czasie O(log N). Kopia dwumianowa i sterta Fibonacciego są odmianami sterty binarnej. Te odmiany umożliwiają również skuteczne zjednoczenie.
- Algorytmy wykresowe: Kolejki priorytetowe są szczególnie używane w algorytmach graficznych, takich jak Najkrótsza ścieżka Dijkstry I Minimalne drzewo rozpinające Prima .
- Wiele problemów można skutecznie rozwiązać za pomocą stert. Zobacz na przykład poniższe. A) K’-ty największy element w tablicy . B) Sortuj prawie posortowaną tablicę/ C) Scal K posortowanych tablic .
Powiązane linki:
- Praktyka kodowania na stercie
- Wszystkie artykuły na Heap
- PriorityQueue: Implementacja sterty binarnej w bibliotece Java
