WPROWADZENIE DO CYKLICZNEJ LISTY POŁĄCZONEJ

Co to jest lista połączona cyklicznie?

The cykliczna lista połączona to połączona lista, w której wszystkie węzły są połączone, tworząc okrąg. Na liście połączonej kołowo pierwszy węzeł i ostatni węzeł są ze sobą połączone, tworząc okrąg. Na końcu nie ma NULL.

Okrągła lista połączona

Zasadniczo istnieją dwa typy list połączonych cyklicznie:

Okrągła pojedynczo połączona lista: Na okrągłej liście z pojedynczym łączem ostatni węzeł listy zawiera wskaźnik do pierwszego węzła listy. Przemierzamy cykliczną, pojedynczo połączoną listę, aż dotrzemy do tego samego węzła, od którego zaczęliśmy. Okrągła, pojedynczo połączona lista nie ma początku ani końca. W następnej części żadnego z węzłów nie ma wartości null.

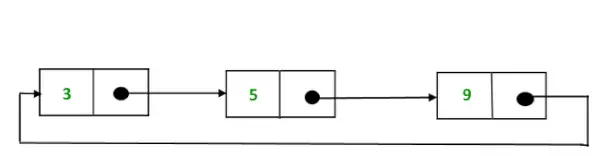
Reprezentacja okrągłej listy pojedynczo połączonej

Okrągła podwójnie połączona lista: Okrągła podwójnie połączona lista ma właściwości zarówno listy podwójnie połączonej, jak i listy połączonej kołowo, w której dwa kolejne elementy są połączone lub połączone poprzednim i następnym wskaźnikiem, a ostatni węzeł wskazuje na pierwszy węzeł za pomocą następnego wskaźnika, a także pierwszy węzeł wskazuje na ostatni węzeł przez poprzedni wskaźnik.

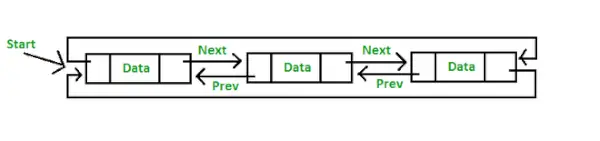
Reprezentacja okrągłej listy podwójnie połączonej

Notatka: Będziemy używać pojedynczo cyklicznej listy połączonej do reprezentowania działania listy połączonej cyklicznie.

Reprezentacja okrągłej listy połączonej:

Listy połączone cyklicznie są podobne do pojedynczych list połączonych, z wyjątkiem połączenia ostatniego węzła z pierwszym węzłem.

Reprezentacja węzła okrągłej listy połączonej:

C++

 // Class Node, similar to the linked list class Node{  int value; // Points to the next node.  Node next; }>

 struct Node {  int data;  struct Node *next; };>

Jawa

 public class Node {  int data;  Node next;    public Node(int data) {  this.data = data;  this.next = null;  } }>

 public class Node {  public int data;  public Node next;    public Node(int data)  {  this.data = data;  this.next = null;  } }>

JavaScript

 class Node {  constructor(data) {  this.data = data;  this.next = null;  } }>

PHP

 class Node {  public $data;  public $next;  function __construct($data) {  $this->dane = $dane;  $this->next = null;  } }>

Python3

 # Class Node, similar to the linked list class Node: def __init__(self,data): self.data = data self.next = None>

Przykład cyklicznej listy pojedynczo połączonej:

Przykład cyklicznej listy połączonej

Powyższą cykliczną, pojedynczo połączoną listę można przedstawić jako:

C++

 // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>

 Node* one = createNode(3); Node* two = createNode(5); Node* three = createNode(9); // Connect nodes one->następny = dwa; dwa->następny = trzy; trzy->następny = jeden;>

Jawa

 // Define the Node class class Node {  int value;  Node next;  public Node(int value) {  this.value = value;  } } // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>

 Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>

JavaScript

 let one = new Node(3); let two = new Node(5); let three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>

PHP

 $one = new Node(3); $two = new Node(5); $three = new Node(9); // Connect nodes $one->następny = dwa dolary; $dwa->następny = $trzy; $trzy->następny = jeden $;>

Python3

 # Initialize the Nodes. one = Node(3) two = Node(5) three = Node(9) # Connect nodes one.next = two two.next = three three.next = one>

Wyjaśnienie: W powyższym programie jeden, dwa i trzy są węzłami o wartościach odpowiednio 3, 5 i 9, które są połączone kołowo jako:

Dla węzła pierwszego: Wskaźnik Next przechowuje adres węzła drugiego.
Dla węzła drugiego: The Next przechowuje adres węzła trzeciego
Dla węzła trzeciego: The Następny wskazuje na węzeł pierwszy.

Operacje na liście połączonej cyklicznie:

Możemy wykonać pewne operacje na liście połączonej cyklicznie, podobnej do listy pojedynczo połączonej, a mianowicie:

Wprowadzenie
Usunięcie

1. Wstawienie do cyklicznej listy połączonej:

Węzeł można dodać na trzy sposoby:

Wstawienie na początku listy
Wstawienie na końcu listy
Wstawienie pomiędzy węzłami

1) Wstawienie na początku listy: Aby wstawić węzeł na początku listy, wykonaj następujące kroki:

Utwórz węzeł, powiedz T.
Utwórz T -> następny = ostatni -> następny.
ostatni -> następny = T.

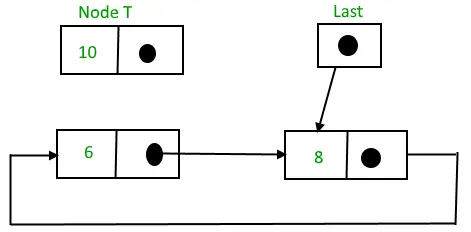
Okrągła lista połączona przed wstawieniem

funkcje Arduino

I wtedy,

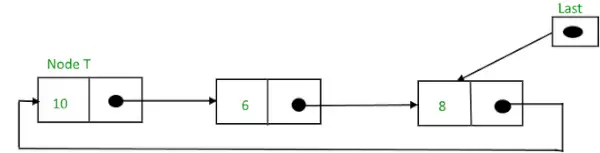
Okrągła lista połączona po wstawieniu

2) Wstawienie na końcu listy: Aby wstawić węzeł na końcu listy, wykonaj następujące kroki:

Utwórz węzeł, powiedz T.
Utwórz T -> następny = ostatni -> następny;
ostatni -> następny = T.
ostatni = T.

Przed włożeniem

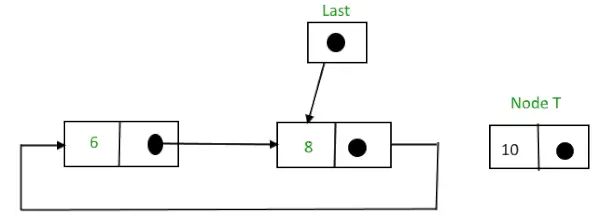
Okrągła lista połączona przed wstawieniem węzła na końcu

przełącznik Javy

Po włożeniu,

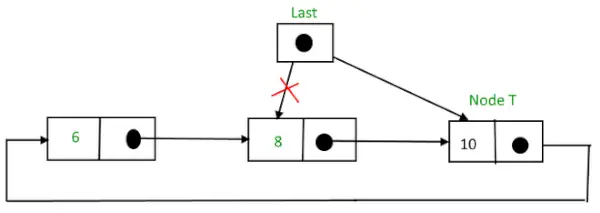
Okrągła lista połączona po wstawieniu węzła na końcu

3) Wstawienie pomiędzy węzłami: Aby wstawić węzeł pomiędzy dwa węzły, wykonaj następujące kroki:

Utwórz węzeł, powiedz T.
Wyszukaj węzeł, po którym należy wstawić T, powiedzmy, że węzeł to P.
Zrób T -> następny = P -> następny;
P -> następny = T.

Załóżmy, że po węźle o wartości 10 należy wstawić liczbę 12,

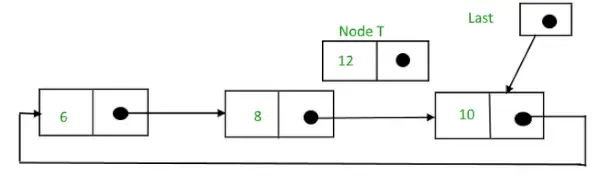
Okrągła lista połączona przed wstawieniem

Po wyszukaniu i wstawieniu,

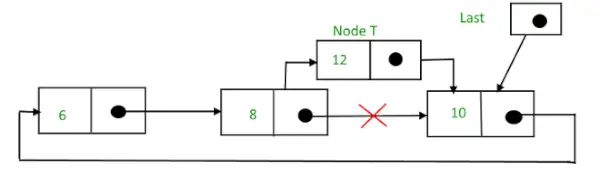
Okrągła lista połączona po wstawieniu

2. Usunięcie z listy połączonej cyklicznie:

1) Usuń węzeł tylko wtedy, gdy jest to jedyny węzeł na liście połączonej cyklicznie:

Zwolnij pamięć węzła
Ostatnia wartość powinna mieć wartość NULL. Węzeł zawsze wskazuje na inny węzeł, więc przypisanie NULL nie jest konieczne.
Jako punkt początkowy można ustawić dowolny węzeł.
Węzły są szybko przemierzane od pierwszego do ostatniego.

2) Usunięcie ostatniego węzła:

Znajdź węzeł przed ostatnim węzłem (niech będzie to temperatura)
Zachowaj adres węzła obok ostatniego węzła w temp
Usuń ostatnie wspomnienie
Na koniec podaj temp

3) Usuń dowolny węzeł z listy połączonej cyklicznie: Otrzymamy węzeł i naszym zadaniem jest usunięcie tego węzła z listy połączonej cyklicznie.

Algorytm:
Przypadek 1 : Lista jest pusta.

Jeśli lista będzie pusta, po prostu wrócimy.

Przypadek 2 :Lista nie jest pusta

Jeżeli lista nie jest pusta to definiujemy dwa wskaźniki prąd I poprzednie i zainicjuj wskaźnik prąd z głowa węzeł.
Przejrzyj listę za pomocą prąd aby znaleźć węzeł do usunięcia i przed przejściem do następnego węzła, za każdym razem ustawiany prev = curr.
Jeśli węzeł zostanie znaleziony, sprawdź, czy jest to jedyny węzeł na liście. Jeśli tak, ustaw head = NULL i free(curr).
Jeśli lista ma więcej niż jeden węzeł, sprawdź, czy jest to pierwszy węzeł listy. Warunek sprawdzenia tego (curr == head). Jeśli tak, przejdź do poprzedniego, aż dotrze do ostatniego węzła. Gdy prev dotrze do ostatniego węzła, ustaw head = head -> next i prev -> next = head. Usuń bieżący
Jeśli curr nie jest pierwszym węzłem, sprawdzamy, czy jest ostatnim węzłem na liście. Warunkiem sprawdzenia jest (curr -> next == head).
Jeśli curr jest ostatnim węzłem. Ustaw prev -> next = head i usuń węzeł curr za pomocą free(curr).
Jeśli węzeł do usunięcia nie jest ani pierwszym, ani ostatnim węzłem, ustaw prev -> next = curr -> next i usuń curr.
Jeśli węzła nie ma na liście, wróć do head i nie rób nic.

Poniżej implementacja powyższego podejścia:

C++

 // C++ program to delete a given key from // linked list. #include  using namespace std; // Structure for a node class Node { public:  int data;  Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(Node** head_ref, int data) {  // Create a new node and make head  // as next of it.  Node* ptr1 = new Node();  ptr1->dane = dane;  ptr1->next = *head_ref;  // Jeśli połączona lista nie ma wartości NULL, // ustaw następny z ostatniego węzła if (*head_ref != NULL) { // Znajdź węzeł przed głową i // zaktualizuj jego następny.  Węzeł* temp = *head_ref;  while (temp->next != *head_ref) temp = temp->next;  temp->następny = ptr1;  } else // Dla pierwszego węzła ptr1->next = ptr1;  *head_ref = ptr1; } // Funkcja wyświetlająca węzły w podanej // cyklicznie połączonej liście void printList(Node* head) { Node* temp = head;  if (głowa != NULL) { wykonaj { cout<< temp->dane<< ' ';  temp = temp->Następny;  } póki (temp != głowa);  } cout<< endl; } // Function to delete a given node // from the list void deleteNode(Node** head, int key) {  // If linked list is empty  if (*head == NULL)  return;  // If the list contains only a  // single node  if ((*head)->dane == klucz && (*head)->next == *head) { free(*head);  *głowa = NULL;  powrót;  } Węzeł *last = *head, *d;  // Jeśli nagłówek ma zostać usunięty if ((*head)->data == klucz) { // Znajdź ostatni węzeł listy while (last->next != *head) last = last->next;  // Wskaż ostatni węzeł następnemu // nagłówkowi, tj. drugiemu węzłowi // listy last->next = (*head)->next;  wolny(*głowa);  *głowa = ostatni->następny;  powrót;  } // Albo węzeł do usunięcia // nie został znaleziony, albo koniec listy // nie został osiągnięty, gdy (last->next!= *head && last->next->data != klucz) { last = last ->dalej;  } // Jeśli odnaleziono węzeł do usunięcia if (last->next->data == klucz) { d = last->next;  ostatni->następny = d->następny;  uwolniony);  } jeszcze cout<< 'Given node is not found in the list!!!
'; } // Driver code int main() {  // Initialize lists as empty  Node* head = NULL;  // Created linked list will be  // 2->5->7->8->10 pchnięcia(&głowa, 2);  push(&głowa, 5);  push(&głowa, 7);  push(&głowa, 8);  push(&głowa, 10);  cout<< 'List Before Deletion: ';  printList(head);  deleteNode(&head, 7);  cout << 'List After Deletion: ';  printList(head);  return 0; }>

 #include  #include  // Structure for a node struct Node {  int data;  struct Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(struct Node** head_ref, int data) {  // Create a new node and make head  // as next of it.  struct Node* ptr1 = (struct Node*)malloc(sizeof(struct Node));  ptr1->dane = dane;  ptr1->next = *head_ref;  // Jeśli połączona lista nie ma wartości NULL, // ustaw następny z ostatniego węzła if (*head_ref != NULL) { // Znajdź węzeł przed głową i // zaktualizuj jego następny.  struktura Węzeł* temp = *head_ref;  while (temp->next != *head_ref) temp = temp->next;  temp->następny = ptr1;  } else // Dla pierwszego węzła ptr1->next = ptr1;  *head_ref = ptr1; } // Funkcja wyświetlająca węzły w podanej // cyklicznie połączonej liście void printList(struct Node* head) { struct Node* temp = head;  if (head != NULL) { do { printf('%d ', temp->data);  temp = temp->następny;  } póki (temp != głowa);  } printf('
'); } // Funkcja usuwająca dany węzeł // z listy void DeleteNode(struct Node** head, int key) { // Jeśli połączona lista jest pusta if (*head == NULL) return;  // Jeśli lista zawiera // tylko pojedynczy węzeł if ((*head)->data == klucz && (*head)->next == *head) { free(*head);  *głowa = NULL;  powrót;  } Węzeł struktury *last = *head, *d;  // Jeśli nagłówek ma zostać usunięty if ((*head)->data == klucz) { // Znajdź ostatni węzeł listy while (last->next != *head) last = last->next;  // Wskaż ostatni węzeł następnemu // nagłówkowi, tj. drugiemu węzłowi // listy last->next = (*head)->next;  wolny(*głowa);  *głowa = ostatni->następny;  powrót;  } // Albo węzeł do usunięcia // nie został znaleziony, albo // koniec listy nie został osiągnięty, gdy (last->next != *head && last->next->data != klucz) { last = last ->dalej;  } // Jeśli odnaleziono węzeł do usunięcia if (last->next->data == klucz) { d = last->next;  ostatni->następny = d->następny;  uwolniony);  } else printf('Podanego węzła nie ma na liście!!!
'); } // Kod sterownika int main() { // Inicjowanie list jako pustej struktury Węzeł* head = NULL;  // Utworzona lista połączona będzie // 2->5->7->8->10 push(&head, 2);  push(&głowa, 5);  push(&głowa, 7);  push(&głowa, 8);  push(&głowa, 10);  printf('Lista przed usunięciem: ');  printList(głowa);  usuńWęzeł(&głowa, 7);  printf('Lista po usunięciu: ');  printList(głowa);  zwróć 0; }>

Jawa

 // Java program to delete a given key from // linked list. import java.io.*; import java.util.*; public class GFG {  /* structure for a node */  static class Node {  int data;  Node next;  };  /* Function to insert a node at the beginning of a Circular linked list */  static Node push(Node head_ref, int data)  {  // Create a new node and make head as next  // of it.  Node ptr1 = new Node();  ptr1.data = data;  ptr1.next = head_ref;  /* If linked list is not null then set the next of last node */  if (head_ref != null) {  // Find the node before head and update  // next of it.  Node temp = head_ref;  while (temp.next != head_ref)  temp = temp.next;  temp.next = ptr1;  }  else  ptr1.next = ptr1; /*For the first node */  head_ref = ptr1;  return head_ref;  }  /* Function to print nodes in a given circular linked list */  static void printList(Node head)  {  Node temp = head;  if (head != null) {  do {  System.out.printf('%d ', temp.data);  temp = temp.next;  } while (temp != head);  }  System.out.printf('
');  }  /* Function to delete a given node from the list */  static Node deleteNode(Node head, int key)  {  if (head == null)  return null;  int flag = 0;  // Find the required node  Node curr = head, prev = new Node();  while (curr.data != key) {  if (curr.next == head) {  System.out.printf(  'Given node is not found in the list!!!
');  flag = 1;  break;  }  prev = curr;  curr = curr.next;  }  // Check if the element is not present in the list  if (flag == 1)  return head;  // Check if node is only node  if (curr == head && curr.next == head) {  head = null;  return head;  }  // If more than one node, check if  // it is first node  if (curr == head) {  prev = head;  while (prev.next != head)  prev = prev.next;  head = curr.next;  prev.next = head;  }  // check if node is last node  else if (curr.next == head) {  prev.next = head;  }  else {  prev.next = curr.next;  }  return head;  }  /* Driver code */  public static void main(String args[])  {  /* Initialize lists as empty */  Node head = null;  /* Created linked list will be 2.5.7.8.10 */  head = push(head, 2);  head = push(head, 5);  head = push(head, 7);  head = push(head, 8);  head = push(head, 10);  System.out.printf('List Before Deletion: ');  printList(head);  head = deleteNode(head, 7);  System.out.printf('List After Deletion: ');  printList(head);  } } // This code is contributed by Susobhan Akhuli>

 using System; // Structure for a node public class Node {  public int data;  public Node next; } // Class for Circular Linked List public class CircularLinkedList {  // Function to insert a node at the  // beginning of a Circular linked list  public static void Push(ref Node head_ref, int data)  {  // Create a new node and make head  // as next of it.  Node ptr1 = new Node();  ptr1.data = data;  ptr1.next = head_ref;  // If linked list is not NULL then  // set the next of last node  if (head_ref != null) {  // Find the node before head and  // update next of it.  Node temp = head_ref;  while (temp.next != head_ref)  temp = temp.next;  temp.next = ptr1;  }  else  // For the first node  ptr1.next = ptr1;  head_ref = ptr1;  }  // Function to print nodes in a given  // circular linked list  public static void PrintList(Node head)  {  Node temp = head;  if (head != null) {  do {  Console.Write(temp.data + ' ');  temp = temp.next;  } while (temp != head);  }  Console.WriteLine();  }  // Function to delete a given node  // from the list  public static void DeleteNode(ref Node head, int key)  {  // If linked list is empty  if (head == null)  return;  // If the list contains only a  // single node  if (head.data == key && head.next == head) {  head = null;  return;  }  Node last = head, d;  // If head is to be deleted  if (head.data == key) {  // Find the last node of the list  while (last.next != head)  last = last.next;  // Point last node to the next of  // head i.e. the second node  // of the list  last.next = head.next;  head = last.next;  return;  }  // Either the node to be deleted is  // not found or the end of list  // is not reached  while (last.next != head && last.next.data != key) {  last = last.next;  }  // If node to be deleted was found  if (last.next.data == key) {  d = last.next;  last.next = d.next;  }  else  Console.WriteLine(  'Given node is not found in the list!!!');  }  // Driver code  public static void Main()  {  // Initialize lists as empty  Node head = null;  // Created linked list will be  // 2->5->7->8->10 Naciśnij (głowica odniesienia, 2);  Naciśnij (głowa ref., 5);  Naciśnij (głowa ref., 7);  Naciśnij (głowa ref., 8);  Naciśnij (głowa odniesienia, 10);  Console.Write('Lista przed usunięciem: ');  PrintList(głowa);  DeleteNode(ref head, 7);  Console.Write('Lista po usunięciu: ');  PrintList(głowa);  } }>

JavaScript

  // Javascript program to delete a given key from linked list.  // Structure for a node  class Node {  constructor() {  this.data;  this.next;  }  }  // Function to insert a node at the  // beginning of a Circular linked list  function push(head, data) {  // Create a new node and make head  // as next of it.  var ptr1 = new Node();  ptr1.data = data;  ptr1.next = head;  // If linked list is not NULL then  // set the next of last node  if (head != null) {  // Find the node before head and  // update next of it.  let temp = head;  while (temp.next != head) temp = temp.next;  temp.next = ptr1;  }  // For the first node  else ptr1.next = ptr1;  head = ptr1;  return head;  }  // Function to print nodes in a given  // circular linked list  function printList(head) {  let tempp = head;  if (head != null) {  do {  console.log(tempp.data);  tempp = tempp.next;  } while (tempp != head);  }  }  // Function to delete a given node  // from the list  function deleteNode(head, key) {  // If linked list is empty  if (head == null) return;  // If the list contains only a  // single node  if (head.data == key && head.next == head) {  head = null;  return;  }  let last = head;  // If head is to be deleted  if (head.data == key) {  // Find the last node of the list  while (last.next != head) last = last.next;  // Point last node to the next of  // head i.e. the second node  // of the list  last.next = head.next;  head = last.next;  return;  }  // Either the node to be deleted is  // not found or the end of list  // is not reached  while (last.next != head && last.next.data != key) {  last = last.next;  }  // If node to be deleted was found  if (last.next.data == key) {  d = last.next;  last.next = d.next;  d = null;  } else console.log('Given node is not found in the list!!!');  }  // Driver code  // Initialize lists as empty  head = null;  // Created linked list will be  // 2->5->7->8->10 głowa = push(głowa, 2);  głowa = push(głowa, 5);  głowa = push(głowa, 7);  głowa = push(głowa, 8);  głowa = push(głowa, 10);  console.log('Lista przed usunięciem: ');  printList(głowa);  usuńWęzeł(głowa, 7);  console.log('Lista po usunięciu: ');  printList(głowa);>

Python3

 # Python program to delete a given key from linked list class Node: def __init__(self, data): self.data = data self.next = None # Function to insert a node at the # beginning of a Circular linked list def push(head, data): # Create a new node and make head as next of it. newP = Node(data) newP.next = head # If linked list is not NULL then # set the next of last node if head != None: # Find the node before head and # update next of it. temp = head while (temp.next != head): temp = temp.next temp.next = newP else: newP.next = newP head = newP return head # Function to print nodes in a given circular linked list def printList(head): if head == None: print('List is Empty') return temp = head.next print(head.data, end=' ') if (head != None): while (temp != head): print(temp.data, end=' ') temp = temp.next print() # Function to delete a given node # from the list def deleteNode(head, key): # If linked list is empty if (head == None): return # If the list contains only a # single node if (head.data == key and head.next == head): head = None return last = head # If head is to be deleted if (head.data == key): # Find the last node of the list while (last.next != head): last = last.next # Point last node to the next of # head i.e. the second node # of the list last.next = head.next head = last.next return # Either the node to be deleted is # not found or the end of list # is not reached while (last.next != head and last.next.data != key): last = last.next # If node to be deleted was found if (last.next.data == key): d = last.next last.next = d.next d = None else: print('Given node is not found in the list!!!') # Driver code # Initialize lists as empty head = None # Created linked list will be # 2->5->7->8->10 głowa = pchnij(głowa, 2) głowa = pchnij(głowa, 5) głowa = pchnij(głowa, 7) głowa = pchnij(głowa, 8) głowa = pchnij(głowa, 10) print('Lista przed usunięciem: ') printList(head) usuńNode(head, 7) print('Lista po usunięciu: ') printList(head)>

Wyjście

List Before Deletion: 10 8 7 5 2 List After Deletion: 10 8 5 2>

Złożoność czasowa: O(N), Najgorszy przypadek ma miejsce, gdy element do usunięcia jest ostatnim elementem i musimy przejść przez całą listę.
Przestrzeń pomocnicza: O(1), Ponieważ używana jest stała dodatkowa przestrzeń.

Zalety okrągłych list połączonych:

Punktem wyjścia może być dowolny węzeł. Całą listę możemy przemierzyć zaczynając od dowolnego punktu. Musimy się tylko zatrzymać, gdy pierwszy odwiedzony węzeł zostanie ponownie odwiedzony.
Przydatne do implementacji kolejki. w odróżnieniu Ten implementacji, nie musimy utrzymywać dwóch wskaźników do przodu i do tyłu, jeśli używamy listy połączonej cyklicznie. Możemy zachować wskaźnik do ostatnio wstawionego węzła, a przód zawsze można uzyskać jako następny od końca.

Listy cykliczne są przydatne w aplikacjach umożliwiających wielokrotne przeglądanie listy. Na przykład, gdy na komputerze PC działa wiele aplikacji, często zdarza się, że system operacyjny umieszcza uruchomione aplikacje na liście, a następnie przegląda je, dając każdej z nich kawałek czasu na wykonanie, a następnie każąc im czekać, aż procesor jest przekazywany innej aplikacji. Dla systemu operacyjnego wygodnie jest używać listy cyklicznej, dzięki czemu po dotarciu do końca listy może ona przejść na początek listy.
Listy cykliczne podwójnie połączone służą do implementacji zaawansowanych struktur danych, takich jak Kopiec Fibonacciego .
Implementacja cyklicznej listy połączonej może być stosunkowo łatwa w porównaniu z innymi, bardziej złożonymi strukturami danych, takimi jak drzewa lub wykresy.

Wady okrągłej listy połączonej:

W porównaniu z listami pojedynczo połączonymi listy cykliczne są bardziej złożone.
Odwracanie listy cyklicznej jest bardziej skomplikowane niż pojedyncze lub podwójne odwracanie listy cyklicznej.
Kod może wejść w nieskończoną pętlę, jeśli nie będzie traktowany ostrożnie.
Trudniej jest znaleźć koniec listy i zapanować nad pętlą.
Chociaż listy połączone cyklicznie mogą być wydajne w niektórych aplikacjach, w niektórych przypadkach ich działanie może być wolniejsze niż w przypadku innych struktur danych, na przykład gdy lista wymaga posortowania lub przeszukania.
Listy połączone cyklicznie nie zapewniają bezpośredniego dostępu do poszczególnych węzłów

Zastosowania okrągłych list połączonych:

Gry wieloosobowe wykorzystują to, aby dać każdemu graczowi szansę na grę.
Okrągłej listy połączonej można używać do organizowania wielu uruchomionych aplikacji w systemie operacyjnym. Aplikacje te są iterowane przez system operacyjny.
Listy połączone cyklicznie można wykorzystać w przypadku problemów z alokacją zasobów.
Listy połączone cyklicznie są powszechnie używane do implementacji buforów cyklicznych,
Listy połączone cyklicznie można używać w symulacjach i grach.

Dlaczego cykliczna lista połączona?

Węzeł zawsze wskazuje na inny węzeł, więc przypisanie NULL nie jest konieczne.
Jako punkt początkowy można ustawić dowolny węzeł.
Węzły są szybko przemierzane od pierwszego do ostatniego.

Następne posty: Okrągła lista połączona | Zestaw 2 (przejście) Okrągła lista pojedynczo połączona | Wprowadzenie Napisz komentarz, jeśli znajdziesz jakiś błąd w powyższym kodzie/algorytmie lub znajdź inne sposoby rozwiązania tego samego problemu

TechCodeview

Co to jest lista połączona cyklicznie?

Reprezentacja okrągłej listy połączonej:

Operacje na liście połączonej cyklicznie:

1. Wstawienie do cyklicznej listy połączonej:

2. Usunięcie z listy połączonej cyklicznie:

Zalety okrągłych list połączonych:

Wady okrągłej listy połączonej:

Zastosowania okrągłych list połączonych:

Dlaczego cykliczna lista połączona?