Mniej niż równe jest koncepcją nierówności, co oznacza, że wyraz po lewej stronie nierówności nie może być większy od wyrazu po prawej stronie, tj. wyraz lewy musi być mniejszy lub maksymalnie równy wyrazowi prawemu. W artykule omówiono pojęcie mniejszego lub równego w matematyce, wprowadzając symbol ≤ i jego przedstawienie na osi liczbowej. Zawiera tabelę symboli matematycznych, problemy praktyczne i odpowiedzi na często zadawane pytania dotyczące nierówności.
Spis treści
pandy idą
- Mniej niż równe do podpisania
- Mniejszy lub równy symbolowi
- Mniejsze lub równe na osi liczbowej
- Oznaczenia symboliczne nierówności
- Mniej niż równy i większy niż równy
Mniej niż równe do podpisania
Na poniższym obrazku dodano znak mniejszości,
Co jest mniejsze lub równe?
Mniejszy lub równy oznacza, że jedna rzecz nie jest większa od drugiej lub może być taka sama. Na przykład, jeśli mamy 2x – 3 ≤ 9, oznacza to, że 2 razy liczba (x) minus 3 nie jest większa niż 9. W uproszczeniu, jeśli dodamy 3 do obu stron, otrzymamy 2x ≤ 12. Następnie dzieląc po obu stronach przez 2, znajdziemy x ≤ 6. Mówimy więc, że liczba (x) może wynosić 6 lub mniej i nadal jest to prawdą.
Sprawdź także
- Mniej niż symbol
- Znak równości
Mniej niż równa przykładowi
Załóżmy, że Jan i Piotr są przyjaciółmi, a wiek Jana jest mniejszy lub równy Piotrowi. Oznacza to, że Jan jest albo młodszy, albo równy Wiekowi Piotra. Innymi słowy, możemy powiedzieć, że Piotr jest albo starszy, albo co najmniej równy wiekowi Jana.
Załóżmy teraz, że wiek Jana wynosi x lat, a Piotra „y” lat, a następnie w formie równania obejmującego mniej niż równe możemy zapisać to jako:
x ≤ y
Gdzie,
- x to wiek Jana
- y to Wiek Piotra
Mniejszy lub równy symbolowi
Symbol mniejszy lub równy. jest ≤
Jest używany w matematyce do porównywania dwóch wielkości. W szczególności, gdy widzisz a ≤ b, oznacza to, że a jest mniejsze lub równe b. Ten symbol łączy w sobie ideę mniejszego niż (<) i równego (=). Oznacza to, że wartość po lewej stronie symbolu jest mniejsza lub taka sama jak wartość po prawej stronie. Pomaga to wyrazić relacje między liczbami lub wyrażeniami matematycznymi, w których jedno może być mniejsze od drugiego lub mu równe.
Mniejsze lub równe na osi liczbowej
Pojęcie mniejszej lub równej na osi liczbowej jest podstawowym wyrażeniem matematycznym używanym do porównywania wartości liczbowych. W tym kontekście oznacza to, że dana liczba jest mniejsza lub równa innej liczbie. Przedstawiając tę zależność na osi liczbowej, w punkcie odpowiadającym mniejszej lub równej wartości umieszcza się zamknięte kółko (=). Na przykład x ≤ 2 jest reprezentowane na osi liczbowej w następujący sposób
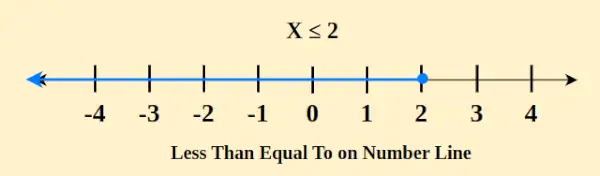
Dodatkowo na prawo od tego punktu rozciąga się linia obejmująca wszystkie liczby większe lub równe wyznaczonej wartości. Włączenie zamkniętego koła służy podkreśleniu, że punkt końcowy jest częścią porównania. Aby to zilustrować, jeśli A ≤ B, punkt A może być umieszczony w punkcie B na osi liczbowej lub na lewo od niego, wskazując, że A jest mniejsze lub równe B, z uwzględnieniem możliwości, że A jest równe B. Ta wizualna reprezentacja pomaga w zrozumieniu względnych wielkości porównywanych wartości.
Oznaczenia symboliczne nierówności
Poniżej dodano stosowane znaki nierówności wraz z ich opisem:
| Notacja symboli nierówności | |
|---|---|
| Opis symbolu | Notacja symboliczna |
| Większy niż znak | > |
| Mniej niż znak | < |
| Równy do podpisania | = |
| Nie równa się podpisowi | ≠ |
| Większe mniejsze lub równe | ≥ |
| Mniejszy lub równy | ≤ |
Mniej niż równy i większy niż równy
Porównanie pomiędzy większym niż równym i mniejszym niż równy, o którym mowa poniżej:
| Różnica między większym niż równym i mniejszym niż równy | ||
|---|---|---|
| Aspekt | Większe niż równe | Mniej niż równe |
| Oznaczający | Wskazuje wartość większą lub minimalną równą podanej wartości | Wskaż wartość mniejszą lub maksymalnie równą podanej wartości |
| Symbol | ≥ | ≤ |
| Przykład | Wiek Ram jest większy niż równy 10 lat ⇒ Wiek Barana ≥ 10 | Wiek Rohanu jest mniejszy niż 15 lat ⇒ Wiek Rohanu ≤ 15 |
Powiązane lektury ,
- Większe niż mniejsze niż
- Większe bądź równe
- Nierówności
Mniej niż równe – przykłady
Przykład 1. Rozwiąż nierówność: 3x – 5 ≤ 10.
Rozwiązanie:
Zacznij od dodania 5 do obu stron:
tekst zawijania css3x ≤ 15
Następnie podziel przez 3: x ≤ 5
Zatem rozwiązaniem jest x ≤ 5
Przykład 2. Rozwiąż nierówność: -2y + 7 ≤ 1.
Rozwiązanie:
Odejmij 7 od obu stron: -2y ≤ -6
Podziel przez -2, pamiętając o odwróceniu znaku nierówności: y ≥ 3
Rozwiązaniem jest y ≥ 3
Mniej niż równe – problemy praktyczne
Wypróbuj następujące ćwiczenia praktyczne oparte na koncepcji „mniejsze niż równe”.
Pytanie 1. Rozwiąż nierówność: 2y – 8 jest mniejsze lub równe 10.
Pytanie 2. Jeśli m wynosi 6, a n wynosi 3, określ, czy m kwadrat minus 5 jest mniejsze lub równe 2n plus 1.
Pytanie 3. Znajdź x: 3x plus 7 jest mniejsze lub równe 22.
Pytanie 4. Jeśli q jest liczbą dodatnią taką, że 4q minus 6 jest mniejsze lub równe 14, znajdź możliwe wartości q.
Pytanie 5. Określ zakres wartości a, które spełniają nierówność 2a plus 5 jest mniejsze lub równe 15.
Mniej niż równe – często zadawane pytania
1. Co jest mniejsze lub równe?
Mniejszy lub równy oznacza relację między dwiema wartościami, co oznacza, że pierwsza wartość jest mniejsza lub równa drugiej.
2. W jaki sposób na osi liczbowej można przedstawić wyrażenie „Mniejszy lub równy”?
Na osi liczbowej tę zależność można wizualnie przedstawić poprzez umieszczenie zamkniętego okręgu (|) na liczbie odpowiadającej mniejszej lub równej wartości i przedłużenie linii w prawo, obejmującej wszystkie liczby większe lub równe tej wartości.
3. Co oznacza zamknięte koło na osi liczbowej?
Zamknięte kółko podkreśla włączenie punktu końcowego do porównania. Jeśli na przykład A ≤ B, oznacza to, że punkt A znajduje się na osi liczbowej lub na lewo od punktu B, uwzględniając możliwość, że A równa się B.
4. Jaki jest przykład rozwiązania nierówności mniejszej lub równej?
Rozważmy nierówność 2x – 3 ≤ 9. Jeśli dodamy 3 do obu stron, otrzymamy 2x ≤ 12. Następnie, dzieląc obie strony przez 2, znajdziemy x ≤ 6. Zatem rozwiązaniem nierówności jest x ≤ 6.
5. Jak rozwiązywać nierówności obejmujące mniejsze lub równe?
Aby rozwiązać nierówności takie jak ax + b ≤ c, zwykłe podejście polega na manipulowaniu nierównością poprzez dodawanie, odejmowanie, mnożenie lub dzielenie w celu wyizolowania zmiennej i określenia zakresu wartości spełniających nierówność.
6. Co to jest symbol mniejszy niż równy i większy niż równy?
Symbol mniej niż równy jest ≤ podczas gdy symbolem większym niż równy jest ≥.
