logo

TechCodeview

Formuły obszaru

Formuły obszaru dla różnych obiektów są wzory używane do wyznaczania pola różnych obiektów. Pole to przestrzeń zajmowana przez granicę dowolnej figury. Wzory powierzchni różnych kształtów geometrycznych zależą od różnych parametrów, takich jak wymiary, wysokość i promień różnych kształtów geometrycznych. Kształty geometryczne są dwojakiego rodzaju:

  • Kształty dwuwymiarowe (kształty 2-D)
  • Kształty trójwymiarowe (kształty 3-D)

W tym artykule będziemy się uczyć o wzorach na pola dla różnych kształtów 2-D i 3-D, takich jak pole prostokąta, pole kwadratu, pole koła, pole sześcianu itp. i inne szczegółowo.

Spis treści



Co to jest obszar?

Przestrzeń zajmowaną przez granicę figury nazywa się polem figury. Mierzy się go w jednostkach kwadratowych. Jednostką SI służącą do pomiaru powierzchni jest m2. Pole powierzchni jest używane w różnych koncepcjach matematycznych, a także w rzeczywistych scenariuszach, takich jak obliczanie powierzchni pokoju, tabeli powierzchni itp. i innych.

Co to są formuły powierzchniowe?

Formuły powierzchniowe to podstawowe narzędzia stosowane w matematyce do obliczania ilości przestrzeni zawartej w różnych dwuwymiarowych kształtach. Wzory te można wykorzystać do znalezienia obszaru geometrycznego figury, takie jak kwadraty, prostokąty, koła, trójkąty, trapezy i elipsy. Korzystając z tych wzorów, możemy dokładnie obliczyć pole o różnych kształtach, co pozwala nam rozwiązywać rzeczywiste problemy i wykonywać ważne obliczenia.

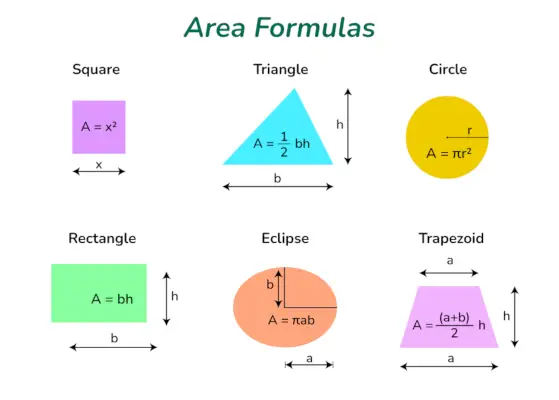
Formuły obszarowe

Formuły obszaru

Co to są kształty 2D?

Kształty, które mają tylko dwa wymiary, nazywane są Kształty 2D . Są one rysowane w przestrzeni 2-D i zależą od 2 parametry, ogólnie długość (l) i szerokość (b). Różne kształty 2-D to, Prostokąt, kwadrat, trójkąt, koła i inne.

Obszar formuły kształtów 2D

Wzory na pole powierzchni 2D to formuły używane do wyznaczania pola różnych kształtów 2D, takiego jak pole trójkąta, pole kwadratu, pole prostokąta, pole rombu itp. Te wzory na pole powierzchni są szeroko stosowane w matematyce do obliczania rozwiązywać różne problemy geometryczne. Różne wzory na pola dla różnych kształtów to:

Wzór pola prostokąta

Prostokąt jest figurą dwuwymiarową który jest czworokątem, czyli ma cztery boki, jego przeciwne boki są równoległe i równe. Wszystkie kąty w prostokącie są równe, a ich miara wynosi 90 stopni. Przekątne prostokąta są równe i są względem siebie symetralnymi.

Wzór na obliczenie pola prostokąta to długość i l i szerokość B Jest,

  • Pole prostokąta (A) = l×b jednostki kwadratowe

Wzór na pole kwadratu

Kwadrat jest figurą dwuwymiarową, która jest czworokątem, to znaczy ma cztery boki, przeciwne strony są równoległe, a wszystkie cztery boki kwadratu są równe. Wszystkie kąty w kwadracie są równe, a ich miara wynosi 90 stopni. Przekątne kwadratu są równe i są względem siebie symetralnymi.

Wzór na obliczenie pola kwadratu o boku A Jest,

  • Pole kwadratu (A) = a 2 jednostki kwadratowe

Wzór na pole trójkąta

Trójkąt jest najprostszym wielokątem utworzonym przez połączenie trzech prostych. Jak sama nazwa wskazuje, jest to wielokąt o trzech kątach. Suma długości wszystkich boków trójkąta to obwód trójkąta, a przestrzeń wewnątrz obwodu trójkąta to pole trójkąta.

Zmień kolor w Gimpie

Wzór na obliczenie pola trójkąta o podstawie B jest i wysokość H Jest,

  • Pole trójkąta (A) = 1/2 × bh kwadrat

Wzór na pole koła

Koło jest figurą geometryczną bez linii prostej. Jest to miejsce punktu znajdującego się zawsze w stałej odległości od punktu stałego. Stały punkt nazywa się środkiem okręgu, a ustalona odległość jest promieniem okręgu.

Wzór na obliczenie obszar koła gdzie r jest promieniem okręgu,

  • Pole koła (A) = πr 2 jednostki kwadratowe

Wzór na pole równoległoboku

Równoległobok jest figurą 2D w którym przeciwne strony są równoległe i równe. Wzór na obliczenie pola równoległoboku o podstawie B i wysokość H Czy,

  • Pole równoległoboku (A) = bh jednostki kwadratowe

Wzór na pole rombu

Romb jest czworokątem, którego wszystkie cztery boki są równe i równoległe, ale nie wszystkie kąty są równe. Wzór na obliczenie pola rombu przez przekątną D 1 I D 2 Czy,

  • Pole rombu (A) = 1/2 × d 1 × zm 2 jednostki kwadratowe

Wzór na pole trapezu

Trapez to inna nazwa trapez . Jest to czworokąt, w którym przeciwne strony są równoległe. Wzór na obliczenie pola trapezu o bokach równoległych A I B i wysokość H Jest,

  • Pole trapezu (A) = 1/2(a +b)h jednostek kwadratowych

Wzór pola elipsy

Elipsa ma kształt 2D i ma przekroje stożkowe. Wzór na obliczenie pola elipsy o osi jak A I B Czy,

  • Pole elipsy (A) = πab kwadrat. jednostek

Wzór na pole półkola

Półkole to figura 2D będąca połową koła. Wzór na obliczenie pola półkola o promieniu r to:

  • Pole półkola (A) = 1/4(πr 2 ) jednostki kwadratowe

Tabela formuł obszaru

Wzory na pola różnych figur 2-D dodano w tabeli dodanej poniżej,

Liczby

Formuła

Zmienne

Prostokąt

Powierzchnia = l×b
  • l to długość
  • b to szerokość

Kwadrat

Powierzchnia = a2

a to bok kwadratu

Trójkąt

Powierzchnia = 1/2×bh
  • b jest podstawą
  • h to wysokość

Koło

Powierzchnia = πr2

r jest promieniem okręgu

Trapez

Pole = 1/2×(a+b)h

świat wumpusa
  • a jest pierwszą podstawą
  • b jest drugą podstawą

Romb

Powierzchnia = 1/2×d1×d2
  • D1jest Jedna Przekątna
  • D2jest drugą przekątną

Równoległobok

Powierzchnia = b × godz
  • b jest podstawą
  • h to wysokość

Elipsa

Powierzchnia = πab
  • a jest promieniem głównej osi
  • b jest promieniem małej osi

Co to są kształty 3D?

Kształty 3D to kształty narysowane w przestrzeniach 3D. Mają 3 wymiary, które są ich parametrami. Powierzchnia tych kształtów zależy od długości, szerokości i wysokości kształtów 3-D. Różne kształty 3D to sześcian, prostopadłościan, walec, stożek, kula i inne. Powierzchnia kształtów 3-D dzieli się na dwie kategorie: powierzchnię zakrzywioną (powierzchnię boczną) {CSA} i powierzchnię całkowitą (TSA). CSA to obszar wszystkich zakrzywionych powierzchni kształtów 3-D, a TSA to obszar wszystkich ścian kształtów 3-D.

Obszar wzoru kształtów 3D

Pole kształtów 3-D to przestrzeń zajmowana przez wszystkie ściany figury. Mierzy się go w jednostkach2. Jednostką pola w układzie SI jest m2. The pole sześcianu , pole prostopadłościanu, pole walca, pole stożka i inne mieszczą się w obszarze kształtów 3D. Dodana poniżej tabela pokazuje wzory różnych figur 3D.

Obszar kształtu

Powierzchnia

Parametry

Powierzchnia sześcianu

6a2

a jest długością krawędzi

Powierzchnia prostopadłościanu

2(lb + lewa + bh)
  • l jest długością krawędzi
  • b jest szerokością krawędzi
  • h jest wysokością krawędzi

Powierzchnia stożka

πr(r + l)
  • r = promień okrągłej podstawy
  • l = wysokość nachylenia

Powierzchnia cylindra

2π(r + h)
  • r = promień okrągłej podstawy
  • h = wysokość cylindra

Powierzchnia kuli

4πr2

r jest promieniem kuli

Powierzchnia półkuli

3πr2

r jest promieniem półkuli

Pole prostopadłościanu

2(wl + hl + hw)
  • l jest długością krawędzi
  • w jest szerokością krawędzi
  • h jest wysokością krawędzi

Sprawdź także

  • Wzory na pole i obwód
  • Wzory na pole powierzchni

Przykłady formuł powierzchniowych

Przykład 1: Znajdź pole prostokąta o długości 5 cm i szerokości 2 cm.

Rozwiązanie:

Dany,

  • Długość prostokąta (l) = 5 cm
  • Szerokość prostokąta (b) = 2 cm

Pole prostokąta (A) = l × b

A = 5 cm × 2 cm
= 10cm2

Przykład 2: Znajdź pole kwadratowego parku, którego bok ma 4 m.

Rozwiązanie:

Dany,

  • Bok kwadratu (a) = 4 m

Pole kwadratu = a2
= (4)2= 16 m2

Zatem powierzchnia kwadratowego parku wynosi 16 m2

Przykład 3: Znajdź pole trójkątnej płyty, której wysokość wynosi 6 cm, a podstawa wynosi 6 cm.

Rozwiązanie:

Dany,

  • Wysokość trójkąta (h) = 6 cm
  • Podstawa trójkąta (b) = 8 cm

Pole trójkąta (A) = 1/2 (b × h)

ZA = 1/2(8 × 6)
= 48/2 = 24 cm2

Pole trójkątnej płytki wynosi 24 cm2

Przykład 4: Znajdź pole okrągłego krążka o promieniu 1,4 cm.

Rozwiązanie:

Dany,

parseint Java
  • Promień okręgu (r) = 1,4 cm

Pole koła(A) = πr2

A = π(1,4)2
= 22/7(1,4)(1,4) = (4,4)(1,4)
= 6,16 cm2

Pole okrągłego krążka wynosi 6,16 cm2

Często zadawane pytania dotyczące formuł obszaru

Co to są formuły powierzchniowe?

Wzory na pole to wzory używane do obliczania pola dowolnej figury. Służy do obliczania ilości miejsca zajmowanego przez figurę. Ogólnie rzecz biorąc, obszar jest oznaczony literą „A”. i jest mierzony w jednostkach2, tj. cm2, M2itp.

Co to jest wzór na pole kwadratu?

Wzór na pole kwadratu to wzór pozwalający obliczyć przestrzeń zajmowaną przez kwadrat. Wzór na obliczenie pola kwadratu to:

Pole kwadratu = (bok) 2

Co to jest wzór na pole prostokąta?

Wzór na pole prostokąta to wzór na obliczenie przestrzeni zajmowanej przez prostokąt. Wzór na obliczenie pola prostokąta to:

Pole prostokąta = długość × szerokość

Co to jest wzór na pole trójkąta?

Wzór na pole trójkąta to wzór na obliczenie przestrzeni zajmowanej przez trójkąt. Wzór na obliczenie pola trójkąta to:

Pole trójkąta = 1/2 (podstawa × wysokość)

Co to jest wzór na pole koła?

Wzór na pole koła to wzór na obliczenie przestrzeni zajmowanej przez okrąg. Wzór na obliczenie pola koła to:

Pole koła = π (promień) 2

Jaki jest wzór na pole czworokąta?

Wzór na obliczenie pola czworokąta,

Pole czworoboku = 1/2 × przekątna 1 × Przekątna 2

Co to jest wzór na pole trójkątnego pryzmatu?

Wzór na pole trójkątnego pryzmatu to:

Pole trójkątnego pryzmatu = (obwód podstawy × długość pryzmatu) + 2 × pole podstawy

Co to jest wzór na pole wielokąta?

Wzór na obliczenie pola wielokąta to:

Powierzchnia wielokąta = 1/2 × (obwód × apotem)

Co to jest wzór na pole trójkąta prostokątnego?

Wzór na pole trójkąta prostokątnego to:

Pole trójkąta prostokątnego = 1/2 × prostopadła × podstawa

Co to jest wzór na pole Pentagonu?

Wzór na powierzchnię Pentagonu to:

Pole Pentagonu = 1/2 × obwód × Apothem