Drzewo binarne jest zrównoważone, jeśli wysokość drzewa wynosi O(Log n), gdzie n jest liczbą węzłów. Na przykład drzewo AVL utrzymuje wysokość O(Log n) upewniając się, że różnica pomiędzy wysokościami lewego i prawego poddrzewa wynosi co najwyżej 1. Drzewa czerwono-czarne utrzymują wysokość O(Log n) upewniając się, że liczba czarnych węzłów na każdej ścieżce od korzenia do liścia jest taki sam i że nie ma sąsiadujących czerwonych węzłów. Zrównoważone drzewa wyszukiwania binarnego są dobre pod względem wydajności, ponieważ zapewniają czas O(log n) na wyszukiwanie, wstawianie i usuwanie.
aes vs des
Zrównoważone drzewo binarne to drzewo binarne spełniające 3 warunki:
- Wysokość lewego i prawego drzewa dla dowolnego węzła nie różni się o więcej niż 1.
- Lewe poddrzewo tego węzła jest również zrównoważone.
- Prawe poddrzewo tego węzła jest również zrównoważone.
Pojedynczy węzeł jest zawsze zrównoważony. Nazywa się je również drzewem binarnym o zrównoważonej wysokości.
Przykład :
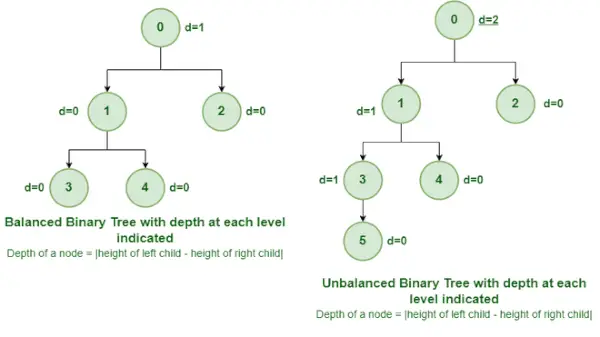
Zrównoważone i niezrównoważone drzewo binarne
Jest to rodzaj drzewa binarnego, w którym różnica między wysokością lewego i prawego poddrzewa dla każdego węzła wynosi 0 lub 1. Na powyższym rysunku węzeł główny o wartości 0 jest niezrównoważony o głębokości 2 jednostek .
Zastosowanie zrównoważonego drzewa binarnego:
- Drzewa AVL
- Czerwone Czarne Drzewo
- Zrównoważone drzewo wyszukiwania binarnego
Zalety zrównoważonego drzewa binarnego:
- Nieniszczące aktualizacje są obsługiwane przez zrównoważone drzewo binarne z tą samą asymptotyczną skutecznością.
- Zapytania o zakres i iteracje we właściwej kolejności są możliwe dzięki zrównoważonemu drzewu binarnemu.
